A munkaközeg potenciális energiát (nyomófej) és mozgási energiát (sebességfej) tartalmaz. A folyadék lehet összenyomható vagy összenyomhatatlan. A turbinák több fizikai elvet alkalmaznak ennek az energiának az összegyűjtésére:
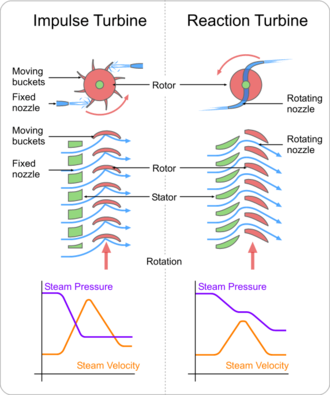
Az impulzusturbinák megváltoztatják a nagy sebességű folyadék vagy gázsugár áramlási irányát. A keletkező impulzus megpörgeti a turbinát, és csökkentett mozgási energiával hagyja el a folyadékáramot. A folyadék vagy gáz nyomása nem változik a turbinalapátokban (a mozgó lapátokban), mint a gőz- vagy gázturbinák esetében, minden nyomáscsökkenés az álló lapátokban (a fúvókákban) történik. Mielőtt elérné a turbinát, a folyadék nyomófeje a folyadék fúvókával történő felgyorsításával sebességfejre változik. A Pelton-kerekek és a de Laval-turbinák kizárólag ezt az eljárást alkalmazzák. Az impulzus-turbináknál nincs szükség a rotor körüli nyomásburkolatra, mivel a folyadéksugarat a fúvóka hozza létre, mielőtt az elérné a rotoron lévő lapátokat. Newton második törvénye leírja az impulzusturbinák energiaátvitelét. Az impulzusturbinák akkor a leghatékonyabbak, ha az áramlás alacsony és a belépő nyomás magas.
A reakciós turbinák a gáz vagy folyadék nyomására vagy tömegére reagálva alakítanak ki nyomatékot. A gáz vagy folyadék nyomása megváltozik, ahogy áthalad a turbina rotorlapátjain. A turbina fokozata(i)ra ható munkafolyadék visszatartásához nyomástartó burkolatra van szükség, vagy a turbinát teljesen be kell meríteni a folyadékáramba (mint például a szélturbináknál). A burkolat tartalmazza és irányítja a munkafolyadékot, és vízturbinák esetében fenntartja a szívócső által keltett szívóerőt. A Francis-turbinák és a legtöbb gőzturbina ezt a koncepciót használja. Összenyomható munkafolyadékok esetében általában több turbinafokozatot használnak a táguló gáz hatékony hasznosítása érdekében. Newton harmadik törvénye leírja a reakcióturbinák energiaátvitelét. A reakcióturbinák jobban alkalmazhatók nagyobb áramlási sebességeknél vagy olyan alkalmazásoknál, ahol a folyadéknyomás (áramlási nyomás) alacsony.
A gőzturbinák esetében, mint amilyeneket tengeri alkalmazásokhoz vagy szárazföldi villamosenergia-termeléshez használnának, egy Parsons-típusú reakcióturbinának körülbelül kétszer annyi lapátsorra lenne szüksége, mint egy de Laval-típusú impulzusturbinának, ugyanolyan mértékű hőenergia-átalakításhoz. Bár emiatt a Parsons-turbina sokkal hosszabb és nehezebb lesz, a reakcióturbina teljes hatásfoka azonos hőenergia-átalakítás mellett valamivel magasabb, mint az egyenértékű impulzus-turbináé.
A gyakorlatban a modern turbinatervek a lehetőségekhez mérten különböző mértékben alkalmazzák mind a reakció-, mind az impulzus-turbina koncepcióját. A szélturbinák egy szárnyaslemezt használnak arra, hogy a mozgó folyadékból reakciófelhajtóerőt hozzanak létre, és azt a rotornak adják át. A szélturbinák a szél impulzusából is nyernek némi energiát a szél szögben történő eltérítésével. A többfokozatú turbinák nagy nyomáson reakció- vagy impulzuslapátot használhatnak. A gőzturbinák hagyományosan inkább impulzusüzeműek voltak, de egyre inkább a gázturbinákhoz hasonló reakciós kialakításúak felé mozdulnak el. Alacsony nyomáson az üzemi közeg térfogata kis nyomáscsökkenés esetén kitágul. Ilyen körülmények között a lapátolás szigorúan reakciótípusúvá válik, és a lapát alja kizárólag impulzusos kialakítású. Ennek oka az egyes lapátok forgási sebességének hatása. A térfogat növekedésével nő a lapát magassága, és a lapát alapja a csúcshoz képest lassabban forog. Ez a sebességváltozás arra kényszeríti a tervezőt, hogy az alapnál lévő impulzusról a nagy reakciójú csúcsra váltson.
A klasszikus turbinatervezési módszereket a 19. század közepén dolgozták ki. A vektorelemzés a folyadékáramlást a turbina alakjával és forgásával hozta összefüggésbe. Eleinte grafikus számítási módszereket alkalmaztak. A turbinaalkatrészek alapvető méreteire vonatkozó képletek jól dokumentáltak, és egy nagy hatékonyságú gépet megbízhatóan lehet tervezni bármilyen folyadékáramlási feltételhez. A számítások egy része empirikus vagy “hüvelykujjszabály” képlet, más része pedig a klasszikus mechanikán alapul. Mint a legtöbb mérnöki számításnál, itt is egyszerűsítő feltételezésekkel éltek.

A turbinafokozat alapvető teljesítményének kiszámításához használhatók a sebességháromszögek. A gáz Va1 abszolút sebességgel lép ki az álló turbina fúvóka vezető lapátjaiból. A rotor U sebességgel forog. A rotorhoz képest a gáz sebessége a rotor bejáratánál Vr1. A rotor elforgatja a gázt, és a rotorhoz képest Vr2 sebességgel lép ki. Abszolút értelemben azonban a rotor kilépési sebessége Va2. A sebességháromszögeket e különböző sebességvektorok felhasználásával alakítjuk ki. A sebességháromszögek a lapát bármely szakaszán (pl.: hub, csúcs, középrész stb.) megkonstruálhatók, de általában az átlagos fokozatsugárnál ábrázolják. A fokozat átlagos teljesítménye kiszámítható a sebességháromszögekből, ezen a sugáron, az Euler-egyenlet segítségével:
Δ h = u ⋅ Δ v w {\displaystyle \Delta h=u\cdot \Delta v_w}}

Így:
Δ h T = u ⋅ Δ v w T {\displaystyle {\frac {\Delta h}{T}}={\frac {u\cdot \Delta v_{w}}{T}}}}

hol:
Δ h {\displaystyle \Delta h}

a fajlagos entalpiaesés a T {\displaystyle T} fokozaton keresztül.

a turbina belépő teljes (vagy stagnálási) hőmérséklete u {\displaystyle u}

a turbina rotor peremsebessége Δ v w {\displaystyle \Delta v_{w}}

az örvénysebesség változása
A turbina nyomásaránya Δ h T {\displaystyle {\frac {\Delta h}{T}}} függvénye

és a turbina hatásfokának függvénye.
A modern turbinatervezés továbbviszi a számításokat. A számítógépes áramlástan eltekint a klasszikus képletek levezetéséhez használt számos egyszerűsítő feltételezéstől, és a számítógépes szoftverek megkönnyítik az optimalizálást. Ezek az eszközök az elmúlt negyven évben folyamatos javulást eredményeztek a turbinatervezésben.
A turbina elsődleges numerikus minősítése a fajlagos fordulatszám. Ez a szám azt a sebességet írja le, amellyel a turbina a teljesítmény és az áramlási sebesség tekintetében a maximális hatásfok mellett működik. A fajlagos fordulatszámot úgy származtatják, hogy az független a turbina méretétől. A folyadékáramlási viszonyok és a kívánt tengelykimeneti fordulatszám ismeretében kiszámítható a fajlagos fordulatszám, és kiválasztható a megfelelő turbinakialakítás.
A fajlagos fordulatszám néhány alapvető képlettel együtt használható egy meglévő, ismert teljesítményű kialakítás megbízható méretezésére egy új, megfelelő teljesítményű méretre.
A tervezéstől eltérő teljesítményt általában turbinatérkép vagy -karakterisztika formájában jelenítik meg.
A rotorban lévő lapátok száma és az állórészben lévő lapátok száma gyakran két különböző prímszám, a felharmonikusok csökkentése és a lapátátmenési frekvencia maximalizálása érdekében.