Calcolare ΔS dai cicli termodinamici
Possiamo anche calcolare un cambiamento di entropia usando un ciclo termodinamico. Come hai imparato in precedenza, la capacità termica molare (Cp) è la quantità di calore necessaria per aumentare la temperatura di 1 mol di una sostanza di 1°C a pressione costante. Allo stesso modo, Cv è la quantità di calore necessaria per aumentare la temperatura di 1 mol di una sostanza di 1°C a volume costante. L’aumento di entropia con l’aumentare della temperatura nella figura \(\PageIndex{2}\) è approssimativamente proporzionale alla capacità termica della sostanza.
Ricorda che la variazione di entropia (ΔS) è legata al flusso di calore (qrev) da ΔS = qrev/T. Poiché qrev = nCpΔT a pressione costante o nCvΔT a volume costante, dove n è il numero di moli di sostanza presente, il cambiamento di entropia per una sostanza la cui temperatura cambia da T1 a T2 è il seguente:
Come scoprirai in corsi di matematica più avanzati di quelli qui richiesti, si può dimostrare che questo è uguale a quanto segue:Per un ripasso dei logaritmi naturali, vedi Essential Skills 6 nel Capitolo 11 “Liquidi”.
\
Similmente,
\
Quindi possiamo usare una combinazione di misure di capacità termica (Equazione 18.20 o Equazione 18.21) e valori misurati sperimentalmente di entalpie di fusione o vaporizzazione se è coinvolto un cambiamento di fase (Equazione 18.18) per calcolare il cambiamento di entropia corrispondente a un cambiamento di temperatura di un campione.
Possiamo usare un ciclo termodinamico per calcolare il cambiamento di entropia quando il cambiamento di fase per una sostanza come lo zolfo non può essere misurato direttamente. Come notato nell’esercizio dell’esempio 6, lo zolfo elementare esiste in due forme (parte (a) nella figura \PageIndex{3}\): una forma ortorombica con una struttura altamente ordinata (Sα) e una forma monoclina meno ordinata (Sβ). La forma ortorombica (α) è più stabile a temperatura ambiente, ma subisce una transizione di fase alla forma monoclina (β) a temperature superiori a 95,3°C (368,5 K). La transizione da Sα a Sβ può essere descritta dal ciclo termodinamico mostrato nella parte (b) della figura \(\PageIndex{3}), in cui lo zolfo liquido è un intermedio. Il cambiamento di entropia che accompagna la conversione dello zolfo liquido in Sβ (-ΔSfus(β) = ΔS3 nel ciclo) non può essere misurato direttamente. Poiché l’entropia è una funzione di stato, tuttavia, ΔS3 può essere calcolato dal cambiamento complessivo di entropia (ΔSt) per la transizione Sα-Sβ, che è uguale alla somma dei valori ΔS per i passi del ciclo termodinamico, utilizzando l’equazione 18.20 e i parametri termodinamici tabulati (le capacità termiche di Sα e Sβ, ΔHfus(α), e il punto di fusione di Sα.)

Solvendo per ΔS3 si ottiene un valore di -3,24 J/(mol-K). Come ci si aspetta per la conversione di uno stato meno ordinato (un liquido) in uno più ordinato (un cristallo), ΔS3 è negativo.
Come si misurano le entropie
L’entropia assoluta di una sostanza a qualsiasi temperatura sopra 0 K deve essere determinata calcolando gli incrementi di calore q richiesti per portare la sostanza da 0 K alla temperatura di interesse, e poi sommando i rapporti q/T. Sono necessari due tipi di misure sperimentali:
- Le entalpie associate a qualsiasi cambiamento di fase che la sostanza può subire nell’intervallo di temperatura di interesse. La fusione di un solido e la vaporizzazione di un liquido corrispondono ad aumenti considerevoli nel numero di microstati disponibili per accettare energia termica, quindi quando questi processi si verificano, l’energia fluisce in un sistema, riempiendo questi nuovi microstati nella misura richiesta per mantenere una temperatura costante (il punto di congelamento o di ebollizione); questi afflussi di energia termica corrispondono ai calori di fusione e vaporizzazione. L’aumento di entropia associato alla fusione, per esempio, è solo ΔHfusione/Tm.
- La capacità termica C di una fase esprime la quantità di calore necessaria per cambiare la temperatura di una piccola quantità ΔT , o più precisamente, di una quantità infinitesimale dT . Così l’aumento di entropia provocato dal riscaldamento di una sostanza in un intervallo di temperature che non comprende una transizione di fase è dato dalla somma delle quantità C dT/T per ogni incremento di temperatura dT . Questo è naturalmente solo l’integrale
\
Perché la capacità termica è essa stessa leggermente dipendente dalla temperatura, le determinazioni più precise delle entropie assolute richiedono che la dipendenza funzionale di C da T sia usata nell’integrale di cui sopra al posto di una costante C.
Quando questo non è noto, si può prendere una serie di misure di capacità termica su stretti incrementi di temperatura ΔT e misurare l’area sotto ogni sezione della curva.
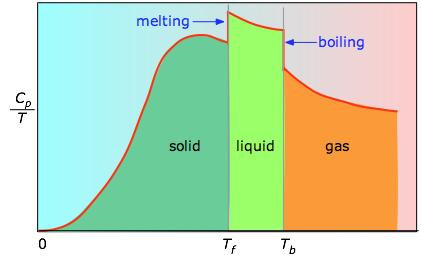
L’area sotto ogni sezione del grafico rappresenta il cambiamento di entropia associato al riscaldamento della sostanza attraverso un intervallo ΔT. A questo devono essere aggiunte le entalpie di fusione, di vaporizzazione, e di qualsiasi cambiamento di fase solido-solido. I valori di Cp per temperature vicine allo zero non sono misurati direttamente, ma possono essere stimati dalla teoria quantistica.
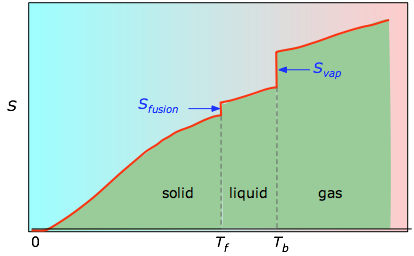
Le aree cumulative da 0 K a qualsiasi temperatura data (prese dal grafico sperimentale a sinistra) sono poi tracciate in funzione di T, e qualsiasi entropia di cambiamento di fase come Svap = Hvap / Tb viene aggiunta per ottenere l’entropia assoluta alla temperatura T.