Nel post di oggi, imparerai la differenza tra numeri primi e composti. Inoltre, vi mostreremo diversi esempi per aiutarvi a capirli meglio.
Index
Cosa sono i numeri primi?
I numeri primi sono i numeri che sono divisibili solo per se stessi e 1, in altre parole, se proviamo a dividerli per un altro numero, il risultato non è un numero intero. Quindi, se si divide il numero per qualsiasi cosa che non sia uno o se stesso, si otterrà un resto che non è zero.
Numeri primi fino a 100
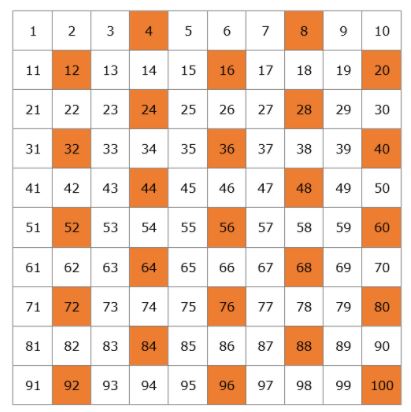
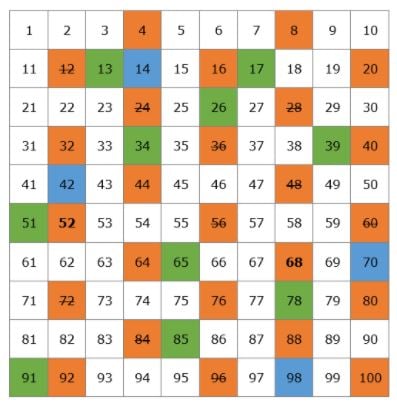
Creeremo una tabella con tutti i numeri primi che esistono fino a 100.
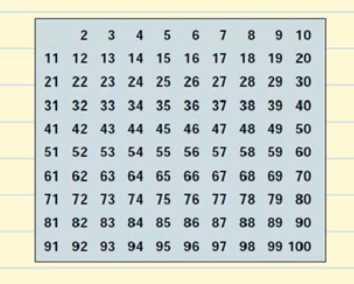
Iniziamo con 2. 2 è un numero primo, ma tutti i multipli di 2 saranno numeri composti perché saranno divisibili per 2. Cancelliamo tutti i multipli di 2 sulla tabella.
Il prossimo numero primo è 3, quindi possiamo cancellare tutti i multipli di 3 perché saranno numeri composti.
Dopo il 3, c’è il prossimo numero primo 5, quindi cancelliamo tutti i multipli di 5.
Poi abbiamo il numero primo 7 e cancelliamo tutti i multipli di 7.
Il prossimo numero primo è 11, quindi cancelliamo tutti i multipli di 11 che sono 22, 33, 44, 55, 66, 77, 88, e 99. Tutti questi numeri erano già stati cancellati, quindi abbiamo finito di cancellare tutti i numeri composti sulla nostra tabella.

Questa è la nostra lista di numeri primi da 1 a 100. Non devi memorizzarli, ma sarebbe meglio se ti ricordassi i numeri più piccoli, come 2, 3, 5, 7, 11, 13.
Quanti numeri primi ci sono?
Il matematico greco Eratostene (III secolo a.C.) ideò un modo veloce per trovare tutti i numeri primi fino a un dato numero. È un procedimento chiamato il Setaccio di Eratostene.
Si noti che tra 1 e 100 ci sono 25 numeri primi. Quanti numeri primi ci sono in totale? Sappiamo fin dall’antichità che ce ne sono una quantità infinita, quindi è impossibile elencarli tutti. Poiché Euclide, che fu il primo a dimostrare che ce n’erano una quantità infinita nel IV secolo a.C., non conosceva il concetto di infinito, disse “i numeri primi sono più di qualsiasi moltitudine fissa di essi”, il che significa che se immagini 100, ce ne sono di più, e se immagini un milione ce ne sono ancora di più.
Numeri primi da 100 a 1.000
Diamo uno sguardo ai numeri primi da 100 a 1.000.
>
Ci dispiace di non poterli mostrare tutti, come sapete ce n’è una quantità infinita. 😉
Esempi di numeri primi
Per aiutarvi a capire meglio i numeri primi, vi spiegheremo un esercizio.
Sara ha 6 pezzi di caramelle che vuole condividere, ma non sa con quante persone può condividerle in modo che tutti abbiano la stessa quantità e non ne rimanga nessuna. In quanti modi può farlo?
Ecco Sara e i suoi 6 pezzi di caramelle:

Come possiamo dividerli?
Il primo e più semplice modo è quello di darli ad una persona, in altre parole, dividere per 1. In questo modo quella persona avrà 6 pezzi di caramelle.
La prossima possibilità è dividerli tra 2 persone. Poiché 6 diviso 2 è 3, ogni persona avrà 3 pezzi di caramelle!

Continuiamo con il prossimo numero, 3. Se dividiamo 6 pezzi di caramelle tra 3 persone è anche una divisione esatta e ogni persona avrà 2 pezzi di caramelle:

Continuiamo con i numeri. Non abbiamo divisioni esatte con 4 e 5, ma le abbiamo con 6.
Siccome 6 diviso 6 è 1, possiamo dare a 6 bambini 1 pezzo di caramella ciascuno.

Raccogliamo alcune informazioni. Abbiamo 6 pezzi di caramelle che possiamo dividere (con una divisione esatta) tra 1, 2, 3 e 6 persone. In altre parole, possiamo dividere il numero 6 e ottenere 0 come resto quando lo dividiamo per 1, 2, 3 e 6. Questi numeri sono conosciuti come i divisori di 6.
Proveremo con un altro numero, 7 per esempio.
Ora Sara ha 7 pezzi di caramelle e vuole dividerle, ma non sa con quante persone può dividerle in modo che tutti abbiano la stessa quantità e non ne rimanga nessuna. In quanti modi può farlo?

Henry è così fortunato! Ha avuto tutti i pezzi di caramella!
Ci sono altri modi per farlo? Non possiamo dividere 7 per 2, 3, 4, 5, o 6, …ma 7 è possibile!
Sara può dividere i pezzi di caramella tra 7 persone, dando loro un pezzo ciascuno:

Quindi 7 può essere diviso solo per 1 e 7, i suoi unici divisori sono 1 e 7. Questi sono i tipi di numeri che chiamiamo numeri primi.
Ci sono altri numeri primi? Certo! Cerchiamone altri:
- E’ 4? No! Perché i suoi divisori sono 1, 2 e 4.
- È il 5? Sì! Perché i suoi divisori sono 1 e 5.
- È 8? No! Perché i suoi divisori sono 1, 2, 4 e 8.
In breve, un numero è primo se ha solo 2 divisori: 1 e se stesso.
Ora puoi cercare molti numeri primi!
Come trovare i numeri primi
Fai attenzione! Vi daremo un trucco per sapere se un numero è primo o no, senza dover cercare i suoi divisori, ma in un modo che è più divertente e ci dà i divisori (se li hanno).
Scegliamo un numero a caso, 16 per esempio.
Per verificare se è un numero primo o no, useremo una tabella che è molto simile alle carte Montessori per moltiplicare. E otterremo tante palline quanto il numero che abbiamo scelto. In questo caso, 16 palline.
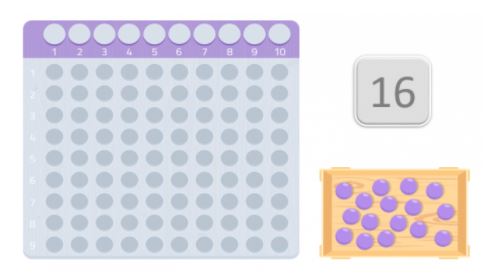
Una volta che abbiamo la tabella e le palline, dobbiamo disporle sul tavolo iniziando dal primo spazio, cercando di formare un rettangolo. I numeri che compongono i bordi del rettangolo sono i divisori di quel numero.
Nel caso in cui riusciamo a formare un rettangolo solo con lo stesso numero che stiamo usando e il numero 1, sarà un numero primo.
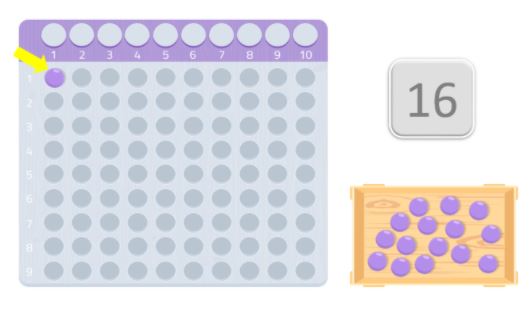
Per esempio, in questo caso, mettiamo 8 palle nella prima fila e altre 8 nella seconda. Come potete vedere, abbiamo formato un rettangolo e possiamo vedere che 8, come 2, sono divisori del numero 16. Quindi, 16 non è un numero primo perché, come sapete, i numeri primi sono quelli che sono divisibili solo per se stessi e per 1.
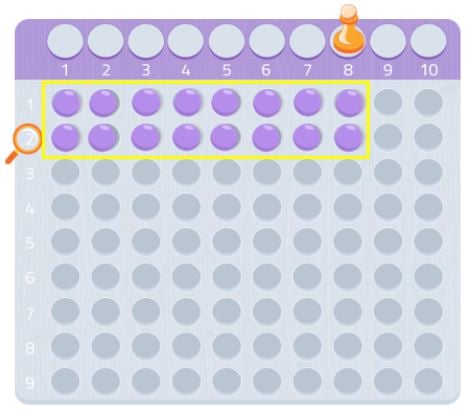
Possiamo provare con un altro numero, 7 per esempio.
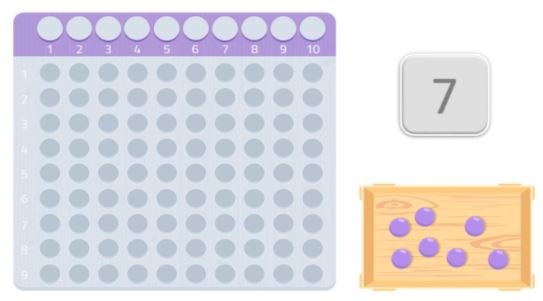
Come possiamo vedere, non potremmo formare un rettangolo completo, ci mancherebbe una palla. Poiché non siamo in grado di formare un rettangolo, potremmo dire che il numero 7 non ha altri divisori tranne se stesso e 1, come possiamo vedere nell’immagine seguente.
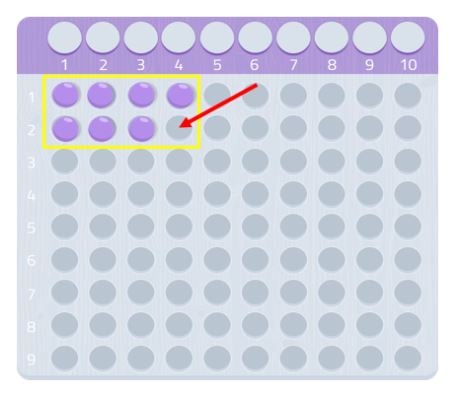
Quindi, 7 è un numero primo!
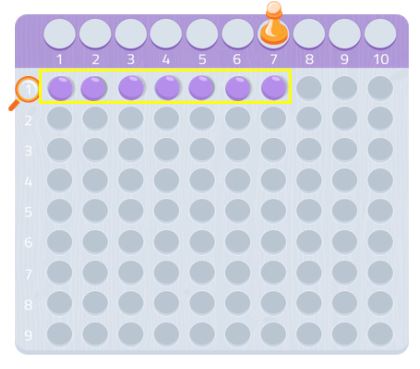
Prova con qualsiasi altro numero, vedrai come funziona! Puoi usare la carta millimetrata e cercare dei rettangoli con quel numero di quadrati.
Perché i numeri primi sono importanti?
I numeri primi sono la chiave dell’aritmetica, di seguito vedrai un esempio che dimostra la loro importanza, non solo in matematica ma anche in natura.
Cosa intendiamo quando diciamo che i numeri primi sono la chiave dell’aritmetica?
Questo perché qualsiasi numero consiste in un prodotto unico formato da una serie di questi numeri.
Si ritiene che siano stati studiati da circa 20.000 anni quando un nostro antenato ha scritto una serie di numeri primi (11, 13, 17 e 19) sull’osso di Ishango. Come se fosse una coincidenza, è stato confermato che gli antichi egizi lavoravano con loro 4.000 anni fa.
Inoltre, la natura li conosce molto bene e alcune specie sono state capaci di scoprirli nel corso della loro evoluzione e di approfittarne per sopravvivere.
Mi riferisco a diverse specie di cicale, come la Magicicada septendecium che vive in Nord America. Questa specie di cicala ha stabilito il suo ciclo di riproduzione intorno ai 13 o 17 anni, non 12, 14, 15, 16 o 18 – esattamente 13 o 17. Questo permette loro di evitare i predatori che hanno anch’essi cicli riproduttivi periodici; immaginate un predatore con un ciclo riproduttivo di 4 anni.
Se il ciclo di vita di una cicala fosse di 12 o 14 anni, coinciderebbe con un predatore molto spesso, molto più che se fosse di 13 o 17 anni. Esattamente 2 volte ogni 100 anni, mentre altrimenti coinciderebbero in 11 cicli che comprometterebbero lo sviluppo della specie.
Anche la sicurezza della comunicazione elettronica si basa sui numeri primi. Ogni messaggio criptato inviato su internet (reti di messaggi, acquisti o banche elettroniche) ha un numero grande associato ad esso, ed è molto difficile sapere se è primo o no. Il destinatario ha uno dei suoi divisori, ed è per questo che può decifrarlo. Quindi avere numeri primi è fondamentale per la nostra privacy quando comunichiamo elettronicamente.
Cosa sono i numeri composti?
I numeri composti sono quei numeri che sono divisibili per 1 e per se stessi e per altri numeri.
Vedremo un esempio di un numero primo e di un numero composto.
11 può essere scritto come la moltiplicazione 1 x 11, ma non può essere scritto come qualsiasi altra moltiplicazione di numeri naturali. Ha solo i divisori 1 e 11, e quindi è un numero primo.
12 può essere scritto come la moltiplicazione 1 x 12 e come la moltiplicazione 3 x 4, e 2 x 6. Poiché 12 è divisibile per più numeri che 1 e se stesso, 12 è un numero composto.
L’1 è un numero primo?
Ci sono persone che lo credono perché dicono che l’1 può essere diviso solo da 1 e se stesso, ma in matematica, il numero 1 è stato scartato come numero primo perché ha solo un divisore. Infatti, il criterio “un numero intero positivo è primo se ha esattamente due divisori positivi” è usato per escludere il numero 1 dalla lista dei numeri primi. Non è perché facciamo gli schizzinosi, ma se il numero uno fosse considerato primo, allora molte proprietà matematiche dovrebbero essere dette diversamente.
Quindi, 1 è un numero composto?
Beh, non è nemmeno composto, poiché non può essere messo come prodotto di numeri primi. Il numero 1 non è né primo né composto. E prima che tu lo chieda, neanche lo zero è primo o composto ma questo perché tutte le considerazioni che stavamo spiegando per i numeri positivi, cioè maggiori di zero.
Divisori di un numero
Il divisore di un numero è il valore che divide il numero in parti esatte, in altre parole, ha un resto di 0.
Come esempio, calcoleremo i divisori per 24.
Iniziamo a dividere con i numeri più piccoli a partire da 1.
- 24 / 1 = 24. Sia 1 che 24 sono divisori.
- 24 / 2 = 12. Quindi 2 e 12 sono divisori.
- 24 / 3 = 8. Quindi 3 e 8 sono divisori.
- 24 / 4 = 6. Quindi 4 e 6 sono divisori.
- 24 / 5 = 4. Non è una divisione esatta e ha un resto di 4 quindi 5 non è un divisore.
Il prossimo numero è 6, ma poiché sappiamo già che 6 è un divisore di 24 abbiamo finito di calcolare i divisori per 24.
Video: Fattorizzazione e numeri primi
Se vuoi saperne di più sui numeri primi e composti, dai un’occhiata al seguente video. Imparerai anche il concetto di fattorizzazione usando la tabella Montessori.
Questo video è uno dei nostri tutorial interattivi e, sebbene non sia interattivo, puoi comunque guardarlo quante volte vuoi e condividerlo con gli amici. Se vuoi accedere ai nostri tutorial interattivi, registrati con Smartick! Il metodo online per aiutare i bambini dai 4 ai 14 anni a imparare e praticare la matematica.
Se vuoi continuare a imparare i numeri primi e la migliore matematica adatta al tuo livello, registrati con Smartick e provalo gratis!
Impara di più:
- I numeri primi e i numeri composti
- I numeri primi: Un trucco per aiutarti a identificarli
- Numeri primi: Come trovarli con il setaccio di Eratostene
- Impara come fattorizzare i numeri primi
- Attività sui numeri primi con Smartick



- Autore
- Post recenti
Un team multidisciplinare e multiculturale composto da matematici, insegnanti, professori e altri professionisti dell’educazione!
Si sforzano di creare i migliori contenuti matematici possibili.
- Esempi di problemi di matematica di 3° grado con soluzioni – 03/25/2021
- Angoli interni consecutivi: Cosa sono e come trovarli con esempi – 03/11/2021
- Esempi di problemi di parola di seconda elementare con soluzioni – 02/04/2021