Si trovano fattoriali in tutta la combinatoria perché è lì che hanno avuto origine. Il fattoriale è stato creato come un modo per esprimere il numero di disposizioni di un gruppo di elementi, che naturalmente troviamo usando, nella sua forma più elementare, la regola di moltiplicazione del conteggio.
Il fattoriale è una sorta di operazione non ufficiale della regola di moltiplicazione del conteggio.
Perché il fattoriale zero è uguale a 1
E’ qui che diventa complicato perché se pensiamo ai fattoriali solo nel contesto in cui sono solitamente definiti, cioè il “prodotto di tutti i fattoriali”.Cioè il “prodotto di tutti i numeri interi positivi minori o uguali al numero” allora capire 0! è come sbattere contro un muro di mattoni.
La maggior parte delle persone ti dirà che 0! è definito come 1, e se chiedi perché ti dicono semplicemente “perché è definito come uno”.
Sì, è piuttosto frustrante. È l’equivalente matematico di chiedere ai tuoi genitori perché devi seguire qualche regola arbitraria che hanno inventato e sentirsi dire “perché l’ho detto io”
Anche se questa potrebbe essere una tecnica accettata dai genitori, è un modo schifoso per imparare la matematica. Quindi qual è il problema? Come abbiamo deciso che il fattoriale zero è uguale a uno?
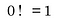
Una comprensione intuitiva
Ricordate come abbiamo detto che il fattoriale ha origine dall’operazione matematica di trovare il numero di permutazioni o disposizioni di un insieme? (Nota: non le permutazioni di un set più piccolo da un set più grande, ma solo le disposizioni di un dato set.)
Il fattoriale zero può essere pensato come il numero di disposizioni di elementi zero in un set, ovvero l’insieme vuoto {}. (Se avete mai studiato gli insiemi, forse nella statistica di base o nella matematica discreta, probabilmente avete familiarità con il concetto di insieme vuoto. È letteralmente l’insieme del nulla.)
Ora se vi chiedessi quante disposizioni ci sono di una cosa rispondereste 1 perché c’è solo un modo di disporre una cosa. Qui segue la stessa idea. La nostra “una cosa” è l’insieme vuoto, e il numero di disposizioni dell’insieme vuoto è uno. Questo è quanto. Ecco perché 0! è uguale a 1.
Come semplificare le espressioni fattoriali
Ora che abbiamo le basi dietro di noi, è il momento del cuore del nostro tutorial fattoriale: semplificare.
Il modo migliore per vedere la matematica è in azione. Quindi eccomi qui per guidarvi attraverso i sei problemi mostrati nell’immagine all’inizio di questo post! Inizieremo in modo semplice, poi passeremo alla formula delle combinazioni con numeri e variabili, e finiremo con alcune espressioni fattoriali più difficili.
❤ STAY CONNECTED ❤
Non perdere un colpo, o un problema di matematica!