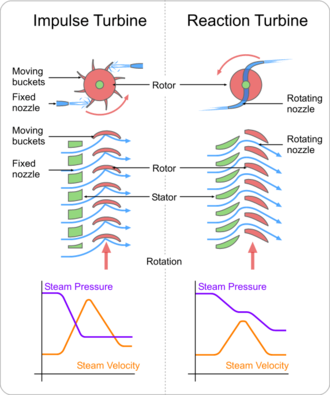
衝動タービンおよび反動タービンの概略図で、ロータは回転部、ステータは固定部。 流体には圧縮性、非圧縮性のものがある。 1189>
インパルスタービンは、高速の流体またはガスジェットの流れの方向を変更する。 その結果、衝動がタービンを回転させ、運動エネルギーが減少した状態で流体の流れから離れます。 蒸気タービンやガスタービンのようにタービン翼(動翼)で流体や気体の圧力変化がなく、すべての圧力損失は静止翼(ノズル)で発生します。 タービンに到達する前に、ノズルで流体を加速することにより、流体の圧力損失を速度損失に変えます。 ペルトン水車とデラバル水車は、このプロセスのみを採用している。 インパルスタービンは、ローター上のブレードに到達する前にノズルによって流体が噴射されるため、ローターの周囲に圧力ケースメントを設ける必要がない。 ニュートンの第二法則は、衝動式タービンのエネルギー伝達を記述しています。 インパルスタービンは、流量が少なく、入口圧力が高い場合に最も効率よく使用することができます。
反応タービンは、気体または流体の圧力または質量に反応することによってトルクを発生させるものである。 気体または流体の圧力は、タービンローターブレードを通過するときに変化します。 このため、作動流体を封じ込める圧力容器が必要であり、また、風車のように流体中に完全に浸漬させることも必要である。 ケーシングは作動流体を収容して方向付けるとともに、水車の場合はドラフトチューブによる吸引を維持する。 フランシスタービンをはじめ、ほとんどの蒸気タービンがこの方式を採用している。 圧縮性のある作動流体では、膨張するガスを効率よく利用するため、通常、タービンを複数段使用する。 反動タービンは、ニュートンの第三法則に基づくエネルギー伝達を行う。 反応タービンは、流速が速い場合や、流体ヘッド(上流側の圧力)が低い場合に適している。
船舶用や陸上発電用の蒸気タービンの場合、パーソンズ型反応タービンは、同じ熱エネルギー変換量であれば、デラバル型衝動タービンの約2倍の翼列数を必要とします。 このため、パーソンズ型タービンは非常に長く、重くなるが、同じ熱エネルギー変換量であれば、反動タービンの総合効率は同等のインパルスタービンよりわずかに高くなる
実際には、現代のタービン設計では、可能な限り程度の差こそあれ、反動と衝動の両方の概念を使用している。 風力タービンは、翼を使用して移動する流体から反力揚力を発生させ、それをローターに付与する。 また、風車は風を斜めにそらすことで、風の衝動からエネルギーを得ている。 多段式タービンは、高圧で反動翼と衝動翼のいずれかを使用することができる。 蒸気タービンは伝統的に衝動式が多かったが、ガスタービンに使われるような反動式の設計に移行しつつある。 低圧では、作動流体媒体はわずかな圧力低下で体積が膨張する。 このような条件下では,ブレードの基部はもっぱら衝 撃型となり,厳密に反応型設計となる. これは各ブレードの回転速度の影響によるものである. 体積が大きくなるとブレードの高さが高くなり、ブレードの基部の回転速度が先端部に対して相対的に遅くなる。 この回転速度の変化により、設計者は基部の衝動から高反動スタイルの先端へと変更を余儀なくされます。
古典的なタービン設計法は19世紀半ばに開発されました。 ベクトル解析は流体の流れとタービンの形状や回転を関連付けるものであった。 当初は図式的な計算方法が用いられた。 タービン部品の基本寸法に関する公式は十分に文書化されており、どのような流体条件に対しても高効率の機械を確実に設計することができる。 計算には経験則や「経験則」に基づく公式もあれば、古典力学に基づく公式もある。 ほとんどの工学計算と同様に、簡略化した仮定がなされている。

ターボジェットのタービン入口ガイドベーン
タービンステージの基本性能を計算するには、速度三角形を使用することができる。 ガスは静止したタービンノズルガイドベーンから絶対速度Va1で出てくる。 ロータは速度Uで回転しており、ロータに対して、ロータ入口に衝突する気体の速度はVr1である。 気体はローターによって回転され、ローターから相対的に速度Vr2で出てくる。 しかし、絶対的にはローター出口速度はVa2である。 これらの様々な速度ベクトルを用いて、速度三角形が構成される。 速度三角形は、ブレードのどの部分(例えば、ハブ、チップ、中間部など)でも作成できますが、通常は平均ステージ半径で表示されます。 ステージの平均性能は、この半径での速度三角形からオイラー方程式を使用して計算できます:
Δh = u ⋅ Δv w {displaystyle \Delta h=ucdot \Delta v_{w}}

Hence:
Δ h T = u ⋅ Δ v w T {displaystyle {}frac {}Delta h}{T}={frac {}ucdot \Delta v_{w}}{T}}} 。

where:
Δ h {displaystyle \Delta h}.

はステージT{displaystyle T}での比エンタルピーの低下である。

はタービン入口全温度(または停滞温度) u {displaystyle u}

はタービンロータ周速 Δ v w {displaystyle \Delta v_{w}} である。

は旋回速度の変化
タービン圧力比はΔh T {displaystyle {}frac {Delta h}{T}} の関数であり、Δh T {displaystyle {}frac {Delta h}{T}} の関数である。

とタービン効率。
現代のタービン設計では、この計算をさらに進めています。 計算流体力学は、古典的な公式を導き出すために使用される単純化した仮定の多くを取り除き、コンピュータ ソフトウェアは最適化を容易にします。 これらのツールにより、過去40年間、タービン設計は着実に改善されてきました。 この数値は、出力と流量に対する最大効率でのタービンの回転数を表すものである。 比速度は、タービンサイズに依存しないことが導き出されている。 流体条件と所望のシャフト出力速度があれば、比速度を計算し、適切なタービン設計を選択することができます。
比速度は、いくつかの基本公式とともに、性能がわかっている既存の設計を、対応する性能を持つ新しいサイズに確実に拡大するために使用することができます。
設計外の性能は通常、タービンマップまたは特性として表示されます。
ローターのブレード数とステーターのベーン数は、高調波を低減しブレード通過周波数を最大化するために、しばしば異なる二つの素数であります。