半減期

図1. 放射性核種の時間的な減衰を示すグラフ。 線源の質量または放射能（1秒間に起こる崩壊事象の数）が50%になるまでの時間が半減期である。 この画像での半減期は1年である。

半減期とは、ある放射性元素のある量が元の値の半分になるまでに崩壊する時間のことである。 さらに、1つの半減期は、ある線源の放射能が元の値の半分に低下するのにかかる時間である。 熱力学第二法則、特に無秩序の記述は、なぜ放射性崩壊が起こるのかを理解するのに役立ちます。 この法則は、閉じた系のエントロピーは決して減少しない、つまり、物事は秩序ではなく、無秩序にさらに落ち込んでいかなければならない、というものです。 このプロセスは「崩壊」として知られており、第二法則は、なぜ物質が時間の経過とともに組織化されていない状態に分解されていくのかを明らかにするのに役立つ。 このプロセスの一部には、放射性崩壊として知られるある測定可能な割合で、新しい、異なる種類の原子に分解するある種の原子が含まれる

すべての放射性物質はその中に不安定な原子核を持っている。 さらに、物質の中にはすでに安定した状態にある原子核もありますが、試料中の安定した原子核と不安定な原子核の比率はさまざまです。 試料中の安定核は不変（エネルギー的に安定した状態）ですが、不安定核は時間の経過とともに何らかの核崩壊を起こし、安定した状態になります。 その結果、何らかの放射線が放出される。 半減期は時間の尺度なので、この安定なエネルギー状態への減少がどれくらいの時間を要するかを決める値です。

物質によって放射能の減衰が早いものとそうでないものがある。 いくつかの放射性元素は、その不安定な原子核の半分が1秒未満で崩壊することがあります。 例えば、クリプトン-101の半減期は約1千万分の1秒です。 一方、半減期が非常に長く、崩壊するまでに何十億年もかかる元素もあります。 ウラン238の半減期は45億1000万年です。 つまり、ウラン238が崩壊して、ウラン238とトリウム234の割合が半分ずつになるまでには、数十億年かかるということです。

方程式

ある放射性物質がある時間経過後にどれだけ残っているかを決めるためによく使われる方程式がある。 これは、その物質の半減期や、最初にどれだけの物質があったかという特性から決定されます。 使用される方程式は、

ここで、

• は時間が経過した後の物質の量
• は物質の初期量
• は経過した時間
• は物質の半減期

さらに、同様の方程式は、物質の放射能は時間とともに減少することを示すために使用することができる。 これを表す場合、式は次のような形になります：

• は時間経過後の物質の活性
• は物質の初期活性
• は経過した時間
• は物質の半減期

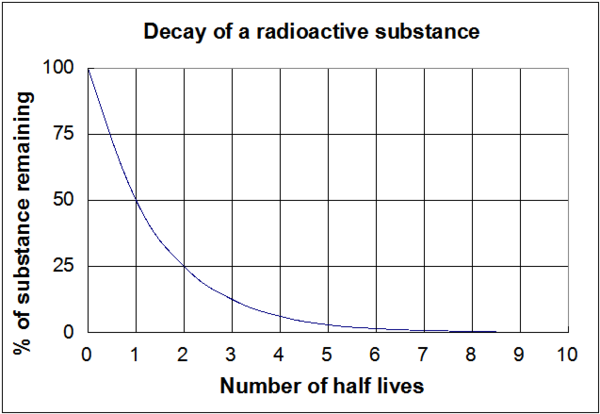
図1に示したグラフはこれらの上記の式で視覚表現されたものです。 半減期の実際の長さ（それが何百万年であろうと、数ナノ秒であろうと）に関係なく、グラフの形は同じになることに注意することが重要です。

半減期の知識は、地質学者が放射性同位元素年代測定法で岩石の年代を決定する方法の一部です。