Dependent vs Independent Events
数記事前に確率の話を始めたんです。 1038>
1 つ以上の事象を含む確率の問題に取り組むときはいつでも、事象が依存するか独立するか、つまり、1 つの事象が他の事象の確率を変えるかどうかを自問することから始めてください。 つまり、ある事象が他の事象の確率を変化させるのか、最初の事象が起こることでシステムが変化するのか、ということです。 最初のカードを引いたとき、システムは52の可能な選択肢から2番目のイベントが起こる前に51に変わる)
実生活では、人間は依存関係を常に混同する傾向がある。 例えば、あなたは公平なコインをひっくり返します。 10回連続で表が出た。 次は必ずオモテになると確信している…だろうか?
次のコインが再びオモテになる確率は?
それはやはり1/2だ。 コインを裏返すのは独立した事象です。 言い換えれば、次のフリップの結果は、それまでに起こったことに影響されません。 あたかも初めてコインをはじくかのようなものです。 確率は変化しない。
なぜ、そのとき裏であるべきだと「感じる」のか。
私たちは、個々の事象について考えるのではなく、一緒に考える傾向があります。
前回の確率の授業で、複数の事象をつなげて、それらがすべて起こるようにする場合(「かつ」シナリオ)には、それらの確率を掛け合わせなければならないことを学びました。
各コイン投げは1/2の確率で表が出るので、単純に1/2を11回掛け合わせる必要があります。
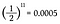
This is a 0.05% chance of flip eleven head in a row!
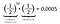
Yes, that’s right.と安堵する前に、11投目で代わりに尾が出る可能性も計算しておきましょう。 10個の頭をはじいた後に1個の尾を引く確率と、11個の頭をはじいた後に1個の尾を引く確率は同じです。 実際、表が出る個々の確率は裏が出る確率と同じなので、11回のコイントスの各配列は同じ可能性0.0005となります。
では…なぜ 10 回連続で頭を出すのは「ありえない」と感じるのでしょうか。
よくある誤解は確率によるものではなく、組合せと順列に関する誤解によるものです。
これまでに、以下のことを立証しました。
- 頭または裏を出す確率は個々の投げごとに同じ確率であること。 p(h) = p(t) = 1/2。
- コイン投げの可能性のあるユニークな配置(順列)は、それぞれ等しい確率です。
では、何が起こるでしょうか。
サンプル空間を理解する
サンプル空間とは、単にすべての結果の配置(順列)のリストです。 11回連続のコイントスの標本空間はかなり大きいので、代わりにもっと簡単なケースを調べてみましょう。
コイン4回投げの標本空間は次の通りです:

直観的には、4回のうち表と裏2回が全部出る方が、表か裏かしか出ないよりありそうだ、と考えるかもしれません。 P(H) = P(T) = 1/2なので、16の順列はそれぞれ同じ確率であることがわかっています。 つまり、各順列の確率は等しい:

注:サンプル空間がすべての可能な結果を表すので、すべての確率の合計は常に1になる(例えば、 0.0625 – 16 = 1).
サンプル空間を見ると、コイン投げの順列は何通りで、表2枚と裏2枚の組み合わせになるか?

16通りのうち6通りで2表/2裏の組み合わせになることに注意します。 これらの6つの順列のどれかが我々の基準を満たすので、これは「または」シナリオとみなされます – なので、確率を足します(または、すべて同じなので単純に6を掛けます)。
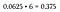
これは、2つの表と裏の組み合わせを投げる確率が 37.5% であり、すべての表またはすべての裏を投げる確率よりもはるかに大きい(これは 6.0% のままです)。1038>
これが、直感的に、1種類をすべて投げるよりも、同じ数の頭と尻尾を投げる方が確率が高いと分かる理由です。 ということで、次はそこへ向かいます!
。