今日の記事では、素数と合成数の違いについて学びます。 さらに、それらをよりよく理解するために、いくつかの例を示します。
Index
What Are Prime Numbers?
素数とは、自分と1でしか割り切れない数、言い換えれば、他の数で割ろうとすると、結果が整数でなくなる数のことです。 つまり、1か自分以外の数で割ると、0ではない余りが出てきます。
100までの素数
これから、100まで存在する素数の表を作ります。
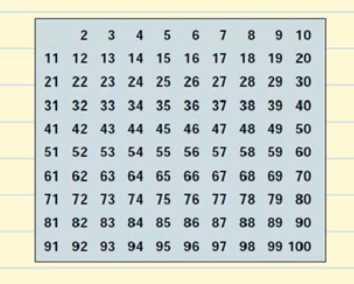
まずは2から見ていきましょう。 2は素数ですが、2の倍数は2で割り切れるので、すべて合成数になります。表から2の倍数をすべて消します。
次の素数は3なので、3の倍数は合成数になるので、すべて消せばよいでしょう。
次の素数は5なので、5の倍数をすべて消します。
次に素数7があるので、7の倍数をすべて消します。
次の素数は11なので、11の倍数である22、33、44、55、66、77、88、99をすべて消します。 5260>

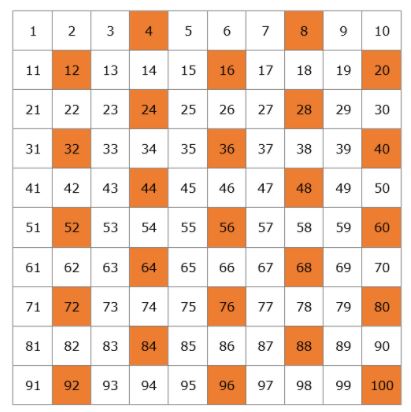
これが1~100までの素数のリストです。 暗記する必要はありませんが、2、3、5、7、11、13のような小さい数字を覚えておくとよいでしょう。
素数はいくつあるか?
ギリシャの数学者エラトステネス(紀元前3世紀)は、任意の数までのすべての素数を素早く見つける方法を考案しました。 5260>
1~100の間に25個の素数があることに注目しましょう。 全部でいくつの素数があるのでしょうか。 古来より無限にあることがわかっていますので、すべてを列挙することは不可能です。 紀元前4世紀に初めて無限にあることを示したユークリッドは、無限の概念を知らなかったので、「素数はどんな決まった数よりも多い」と言ったそうですが、100を想像したらもっと多く、100万を想像したらもっと多いという意味です。

ご存知のように無限にあるので、すべてを紹介できないのが残念です。 😉
素数の例
素数の理解を深めるために、練習問題を解説していきます。
サラが分けたいお菓子を6個持っているが、何人に分ければ全員が同じ量を食べられ、残りがないのかがわからない。
ここにサラと彼女の6個のキャンディがあります:

どのように分けることができますか?
最初の最も簡単な方法は、1人に与えること、言い換えれば1で割ります。 6個を2で割ると3個になるので、一人3個のキャンディを手に入れることができます!

次の数字、3について続けます。 6個のキャンディを3人で割ると、これも正確に分割でき、一人2個のキャンディを手に入れます:

続いて数字を見てみましょう。 5260>
6を6で割ると1になるので、6人の子供に1個ずつお菓子をあげられます。

これから情報を集めます。 6個のお菓子があるので、1人、2人、3人、6人に(正確に分けて)配ることができます。 つまり、6という数字を1、2、3、6で割ると余りとして0ができる。
ここで、サラは7個のキャンディを持っていて、それを分けたいのですが、何人で分ければ全員が同じ量を食べられ、残りがないのかがわかりません。

Henry はとてもラッキーです! 彼はすべてのキャンディーを手に入れました!
他のやり方はありますか? 7を2、3、4、5、6で割ることはできませんが、7は可能です!
サラはキャンディのかけらを7人で分けて、1個ずつあげることができます:

だから7は1と7でしか割れません、その約数は1と7だけです。 これが素数と呼ばれる種類の数字です。
素数はもっとたくさんあるのですか。 もちろんです。
- 4は? いいえ、ありません。 その約数は1、2、4ですから。
- 5は? はい!です。
- 8は? いいえ!
要するに、ある数が2つの約数しか持たない場合、その数は素数である。 5260>
これで、たくさんの素数を探すことができます!
How to Find Prime Numbers
よく見てください!
How to Find Prime Numbers
How to Find Prime Numbers
How to Find Prime Numbers ! ある数字が素数かどうか、その約数を探さなくても、もっと楽しく、約数(があれば)を知ることができるコツをお伝えします。
ランダムに数字を選んでみましょう。たとえば16。
素数かどうか調べるには、モンテッソーリのカードによく似た表を使って掛け算をしていきます。 そして、選んだ数字と同じ数だけボールを用意します。 この場合、16個のボールです。
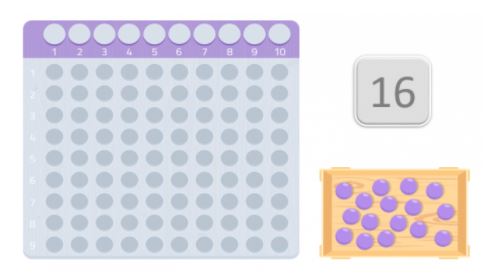
テーブルとボールを用意したら、最初のスペースから順にテーブルに置き、長方形を形成するようにしましょう。
万が一、今使っている数字と同じ数字と1だけで長方形を作ることができたら、それは素数です。
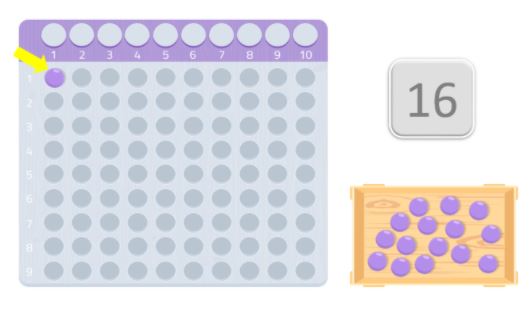
例えば、この場合、1列目に8球、2列目にさらに8球置くことになります。 ご覧のように長方形を形成していますが、8個は2個と同じく16個の約数であることがわかります。 したがって、16は素数ではありません。ご存知のように、素数とは自分自身と1でしか割り切れない数です。
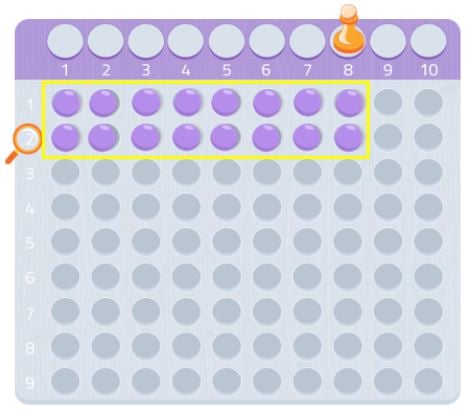
別の数、たとえば7で試してみましょう。
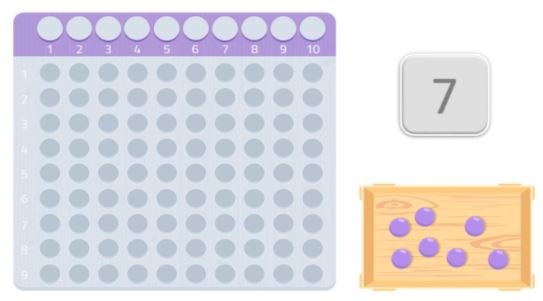
見てわかるように、完全な長方形を作ることはできず、ボールが1つ足りません。 長方形を作ることができないので、次の画像のように、数7は自分自身と1以外の約数を持たないと言えます。
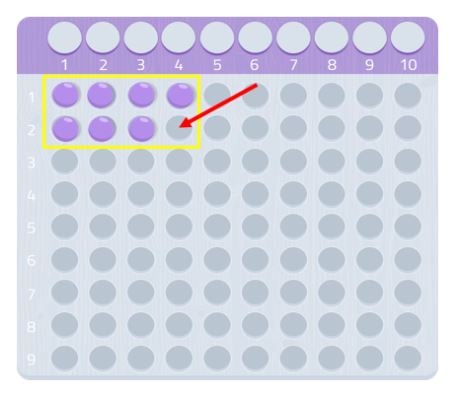
したがって、7は素数です!
他の数でも試してみてください。 グラフ用紙を使い、その数の正方形を使った長方形を探すことができます。
なぜ素数は重要なのか?
素数は算数の鍵です。以下は、数学だけでなく自然界でもその重要性を示す例です。
素数が算数の鍵というのは、どういう意味でしょうか?
これは、どんな数も、これらの数の連なりからなる一意の積で成り立っているからです。
素数の研究は約2万年前から行われており、私たちの祖先がイシャンゴ骨に11、13、17、19の素数群を書き留めたのが始まりと考えられています。
さらに、自然は素数をよく知っていて、進化の過程で素数を発見し、生存に役立てた種もある
北米に生息するマジカダ・セプテンデシウムなど、いくつかのセミの種を指している。 この種のセミは、12年、14年、15年、16年、18年ではなく、ちょうど13年か17年頃に繁殖サイクルを確立しているのです。 これによって、同じく周期的な繁殖サイクルを持つ捕食者を避けることができます。4年の繁殖サイクルを持つ捕食者を想像してみてください。
セミのライフサイクルが12年か14年だった場合、捕食者と重なる頻度は、13年か17年の場合よりも非常に高くなるでしょう。 100年にちょうど2回、そうでない場合は11回の周期で重なり、種の発展を危うくする。 インターネット上で送信される暗号化されたメッセージ(メッセージネットワーク、購入、電子バンキング)には、すべて大きな数字が関連しており、それがどこの素数かどうかを知ることは非常に困難です。 受信者はその約数の一つを持っているからこそ、復号化できるのです。 5260>
合成数とは何か?
素数と合成数の例を見てみましょう。
11は1×11の掛け算として書くことができますが、他の自然数の掛け算としては書けません。 5260>
12 は1×12の掛け算と3×4、2×6の掛け算で書けるが、1と自分以外の数で割り切れるので、12は合成数である。
1は素数か
1は1と自分でしか割り切れないというのでそう考える人がいますが、数学では1は割り算が1つしかないので素数として捨てられてきました。 実際、「正の整数は、正の約数をちょうど2つ持っていれば素数である」という基準で、素数リストから1を除外している。 5260>
では、1は合成数なのですか?
まあ、素数の積として置くことはできないので、合成数でもないのですが。 1という数字は素数でも合成数でもないのです。 5260>
数の約数
数の約数とは、数を正確に分割する値、言い換えれば、余りが0であることを意味します。
例として、24の約数を計算します。
まず、1から順に小さい数から割っていきます。
- 24 / 1 = 24。 1も24も約数です。
- 24 / 2 = 12。 つまり2と12は約数です。
- 24 / 3 = 8。つまり3と8は約数です。
- 24 / 4 = 6。つまり4と6は約数です。
- 24 / 5 = 4. 正確な除算ではなく、余りが4なので、5は約数ではありません。
次の数は6ですが、6が24の約数であることは既に分かっているので、24の約数の計算は終わりました。
ビデオ。 因数分解と素数
素数と合成数についてもっと知りたい方は、次のビデオを見てください。 また、モンテッソーリ表を使って因数分解の概念を学びます。
このビデオはインタラクティブチュートリアルの1つで、インタラクティブではありませんが、何度でも見ることができ、友達と共有することも可能です。 インタラクティブなチュートリアルにアクセスしたい場合は、Smartickに登録してください。 4歳から14歳の子供たちが数学を学び、実践するためのオンラインメソッドです。
素数や自分のレベルに合わせた最高の数学について学習を続けたい場合は、Smartickに登録して無料でお試しください!
さらに学ぶ:
- 素数と合成数
- 素数.Numbers.Prime.Prime.Numbers.Prime.Pur.Prime.Pur.Pur.Prime.Prime.Per.Per.Per.Per.Per: 見分けるコツ
- Prime Numbers: エラトステネスの篩で見つける方法
- 素数の因数分解を学ぶ
- Smartickを使った素数のアクティビティ



- 著者
- 最近の投稿
数学者、教師、教授など教育の専門家からなる、学際的かつ多文化的なチームです!
最高の数学コンテンツを作るために努力しています。
- 3年生の数学単語問題の例と解答 – 03/25/2021
- 連続した内角。 その正体と求め方 例題付き – 03/11/2021
- 中学2年生の単語問題の例題と解答 – 02/04/2021