Logistic Regression

Logistic regression (aka logit regression or logit model) は1958年に統計学者 David Cox が開発した、応答変数 Y がカテゴリである回帰モデルである。 ロジスティック回帰は、1つ以上の予測変数（X）に基づいて、カテゴリカルな反応の確率を推定することができます。 それは，予測変数の存在が，ある結果の確率を特定のパーセンテージで増加（または減少）させることを言うことができる． このチュートリアルは、Yがバイナリである場合、つまり、合格/不合格、勝ち/負け、生/死、健康/病気などの結果を表す “0” と “1” の2値のみを取り得る場合について説明します。 従属変数が2つ以上の結果カテゴリを持つケースは，多項ロジスティック回帰で分析されるか，複数のカテゴリが順序づけられる場合，順序ロジスティック回帰で分析されるかもしれない．

tl;dr

このチュートリアルはロジスティック回帰の入門として提供され、次のことをカバーします1：

1. 複製の要件。 このチュートリアルの分析を再現するために必要なもの
2. Why logistic regression:
3. なぜロジスティック回帰を使うのか：データを準備する。
4. モデリングするためにデータを準備する: 単純なロジスティック回帰。 単一の予測変数Xで応答Yの確率を予測する
5. 重ロジスティック回帰: 応答Yの確率を予測する。 複数の予測変数で応答Yの確率を予測する
6. モデル評価& 診断。 モデルがどの程度データに適合しているか？ どの予測変数が最も重要か？

Replication Requirements

このチュートリアルでは、主にISLRパッケージで提供されるDefaultデータを使用します。 これは、顧客がデフォルトしたかどうか、学生かどうか、顧客が持っている平均残高、顧客の収入など、1万人の顧客に関する情報を含むシミュレーション・データセットです。 また、データ操作、可視化、パイプライン・モデリング機能、およびモデル出力の整頓機能を提供するいくつかのパッケージも使用します。

# Packageslibrary(tidyverse) # data manipulation and visualizationlibrary(modelr) # provides easy pipeline modeling functionslibrary(broom) # helps to tidy up model outputs# Load data (default <- as_tibble(ISLR::Default))## # A tibble: 10,000 × 4## default student balance income## <fctr> <fctr> <dbl> <dbl>## 1 No No 729.5265 44361.625## 2 No Yes 817.1804 12106.135## 3 No No 1073.5492 31767.139## 4 No No 529.2506 35704.494## 5 No No 785.6559 38463.496## 6 No Yes 919.5885 7491.559## 7 No No 825.5133 24905.227## 8 No Yes 808.6675 17600.451## 9 No No 1161.0579 37468.529## 10 No No 0.0000 29275.268## # ... with 9,990 more rows

Why Logistic Regression

定性的回答の場合、線形回帰は適切でありません。 なぜそうなのか？ 救急治療室の患者の症状に基づいて病状を予測しようとしているとします。 この単純化された例では，脳卒中，薬物の過剰摂取，てんかん発作の3つの診断がありうる． このコーディングを使って、最小二乗法は予測変数のセットに基づいてYを予測するために線形回帰モデルを適合させるために使用することができます。 残念ながら、このコーディングは、脳卒中とてんかん発作の間に薬物過剰摂取を置き、脳卒中と薬物過剰摂取の差は、薬物過剰摂取とてんかん発作の差と同じであると主張し、結果の順序を意味する。 実際には、そうでなければならない理由は特にない。 例えば、

という同じように妥当なコーディングを選択することも可能で、その場合、3つの状態の間に全く異なる関係があることを意味することになります。

我々のデータにより関連するのは、もし我々が残高に基づいて顧客を高リスクと低リスクの債務不履行者として分類しようとしている場合、線形回帰を使用することができます。 残念ながら、ゼロに近い残高の場合、デフォルトの負の確率を予測し、非常に大きな残高を予測する場合、1 よりも大きな値が得られます。もちろん、クレジットカードの残高に関係なく、デフォルトの真の確率は 0 と 1 の間に入るはずなので、これらの予測は賢明ではありません。

データの準備

回帰のチュートリアルのように、我々はデータをトレーニング（60%）とテスト（40%）に分割し、我々のモデルがサンプル外のデータセットでどれだけうまく機能するかを評価することができるようにします。

set.seed(123)sample <- sample(c(TRUE, FALSE), nrow(default), replace = T, prob = c(0.6,0.4))train <- defaulttest <- default

単純ロジスティック回帰

顧客の平均残高に基づくデフォルトの確率を予測するために、ロジスティック回帰モデルを適合させる予定です。 glm関数は、ロジスティック回帰を含むモデルのクラスである一般化線形モデルに適合させます。 glm 関数の構文は lm と似ていますが、他の一般化線形モデルではなく、ロジスティック回帰を実行するよう R に指示するために、引数 family = binomial を渡さなければならない点が異なります。 ロジスティック回帰モデルを適合させるために最尤法を使用する基本的な直観は次の通りです：我々は、式（1）を使用して、各個人のデフォルトの予測確率が、個人の観察されたデフォルト状態にできるだけ近く対応するように、およびの推定値を求めます。 言い換えれば、式（1）で与えられたp（X）のモデルにこれらの推定値を差し込むと、デフォルトしたすべての個人について1に近い数値が得られ、そうでないすべての個人についてゼロに近い数値が得られるようなandを見つけようとするのである。 この直感は、尤度関数と呼ばれる数式を用いて公式化することができる。

推定値および推定値は、この尤度関数を最大化するように選択される。 最尤法は、今後のチュートリアルで検討する非線形モデルの多くを適合させるのに使用される非常に一般的なアプローチです。

default %>% mutate(prob = ifelse(default == "Yes", 1, 0)) %>% ggplot(aes(balance, prob)) + geom_point(alpha = .15) + geom_smooth(method = "glm", method.args = list(family = "binomial")) + ggtitle("Logistic regression model fit") + xlab("Balance") + ylab("Probability of Default")

線形回帰と同様に、summaryまたはglanceを使ってモデルを評価することができます。 係数出力の形式は線形回帰で見たものと似ていますが、summaryの下部にある適合度の詳細が異なることに注意してください。 これについては後で詳しく説明しますが、devianceという単語があることだけは注意してください。 デビアンスは、線形回帰における二乗和の計算と類似しており、ロジスティック回帰モデルにおけるデータへの適合度の低さを表す指標です。 ヌル・デビアンスは、切片のみのモデル（つまり「予測変数なし」）と飽和モデル（理論的に完全に適合するモデル）の差を表しています。 目標は、モデルのデビアンス（残留デビアンスと表記）が低くなることであり、値が小さいほど適合度が高いことを示している。 この点で、ヌルモデルは、予測モデルを比較するためのベースラインを提供します。

summary(model1)## ## Call:## glm(formula = default ~ balance, family = "binomial", data = train)## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -2.2905 -0.1395 -0.0528 -0.0189 3.3346 ## ## Coefficients:## Estimate Std. Error z value Pr(>|z|) ## (Intercept) -1.101e+01 4.887e-01 -22.52 <2e-16 ***## balance 5.669e-03 2.949e-04 19.22 <2e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## (Dispersion parameter for binomial family taken to be 1)## ## Null deviance: 1723.03 on 6046 degrees of freedom## Residual deviance: 908.69 on 6045 degrees of freedom## AIC: 912.69## ## Number of Fisher Scoring iterations: 8

係数の評価

以下の表は、バランスを使用してデフォルト = Yes の確率を予測するためにロジック回帰モデルをフィットした結果の係数推定値と関連情報である。 ロジスティック回帰からの係数推定値は、予測変数と応答変数の間の関係を対数オッズスケールで特徴づけることに留意してください（詳細はISLR1の第3章を参照してください）。 したがって、これは、残高の増加がデフォルトの確率の増加と関連していることを示す。 正確には、残高が1単位増加すると、デフォルトの対数オッズが0.0057単位増加することと関連する。

tidy(model1)## term estimate std.error statistic p.value## 1 (Intercept) -11.006277528 0.488739437 -22.51972 2.660162e-112## 2 balance 0.005668817 0.000294946 19.21985 2.525157e-82

我々はさらに残高係数を、-毎月の保有残高が1ドル増加するごとに、顧客がデフォルトする確率は1倍増加する、と解釈することができる。0057.

exp(coef(model1))## (Intercept) balance ## 1.659718e-05 1.005685e+00

係数出力の多くの側面は、線形回帰出力で議論したものと同様である。 例えば、我々は、それらの標準誤差を計算することによって、係数推定値の信頼区間と精度を測定することができます。 例えば、p値< 2e-16は、持ち越し残高とデフォルトの確率の間に統計的に有意な関係があることを示唆しています。 また、線形回帰のチュートリアルで行ったように、標準誤差を使用して信頼区間を得ることができます：

confint(model1)## 2.5 % 97.5 %## (Intercept) -12.007610373 -10.089360652## balance 0.005111835 0.006269411

Making Predictions

係数が推定されると、任意のクレジットカード残高のデフォルト確率を計算することは簡単なことです。 数学的には、我々のモデルからの係数推定値を使用して、1,000ドルの残高を持つ個人のデフォルト確率は0.5%未満であると予測されます

我々は、predict関数（type = "response"を必ず含む）を使用してRでデフォルトの確率を予測することができます。 ここでは、1000ドルと2000ドルの残高に基づくデフォルトの確率を比較しています。 残高が 1000 ドルから 2000 ドルになると、デフォルトの確率は 0.5% から 58% へと大幅に増加します！

predict(model1, data.frame(balance = c(1000, 2000)), type = "response")## 1 2 ## 0.004785057 0.582089269

また、ロジスティック回帰モデルで定性的予測子を使用することもできます。

model2 <- glm(default ~ student, family = "binomial", data = train)tidy(model2)## term estimate std.error statistic p.value## 1 (Intercept) -3.5534091 0.09336545 -38.05914 0.000000000## 2 studentYes 0.4413379 0.14927208 2.95660 0.003110511

predict(model2, data.frame(student = factor(c("Yes", "No"))), type = "response")## 1 2 ## 0.04261206 0.02783019

多重ロジスティック回帰

式で見られるように、我々はまた我々のモデルを拡張することができます。 ここでp個の予測変数は次のとおりです：

それでは、残高、収入（千ドル単位）、および学生身分変数に基づいてデフォルトの確率を予測するモデルを当てはめてみましょう。 ここで、意外な結果があります。 残高とstudent=Yesの状態に関連するp値は非常に小さく、これらの変数のそれぞれがデフォルトの確率に関連していることを示しています。 しかし、学生変数の係数は負であり、学生は非学生よりもデフォルトする確率が低いことを示している。 一方、学生の地位のみに基づいてデフォルトの確率を予測したモデル 2 では、学生変数の係数は、学生の方がデフォルトの確率が高いことを示しています。 何が原因か？

model3 <- glm(default ~ balance + income + student, family = "binomial", data = train)tidy(model3)## term estimate std.error statistic p.value## 1 (Intercept) -1.090704e+01 6.480739e-01 -16.8299277 1.472817e-63## 2 balance 5.907134e-03 3.102425e-04 19.0403764 7.895817e-81## 3 income -5.012701e-06 1.078617e-05 -0.4647343 6.421217e-01## 4 studentYes -8.094789e-01 3.133150e-01 -2.5835947 9.777661e-03

この矛盾の説明は、下図の右側のパネルで説明できます。 学生と残高という変数には相関がある。 学生は負債を多く抱える傾向があり、それがデフォルトの確率を高くしている。 つまり、学生はクレジットカードの残高が多く、下図の左側のパネルでわかるように、デフォルト率が高くなる傾向がある。 したがって、あるクレジットカードの残高を持つ個々の学生は、同じクレジットカードの残高を持つ非学生よりもデフォルトの確率が低い傾向にあるとしても、学生全体がクレジットカードの残高を多く持つ傾向があるということは、全体として学生が非学生よりも高い確率でデフォルトする傾向にあることを意味する。 これは、クレジットカード会社にとって、どのような人に信用を提供すべきかを判断する上で重要な違いである。 学生のカード残高に関する情報がない場合、学生は非学生よりもリスクが高い。 しかし、その学生は、同じクレジットカードの残高を持つ非学生よりもリスクが低い！

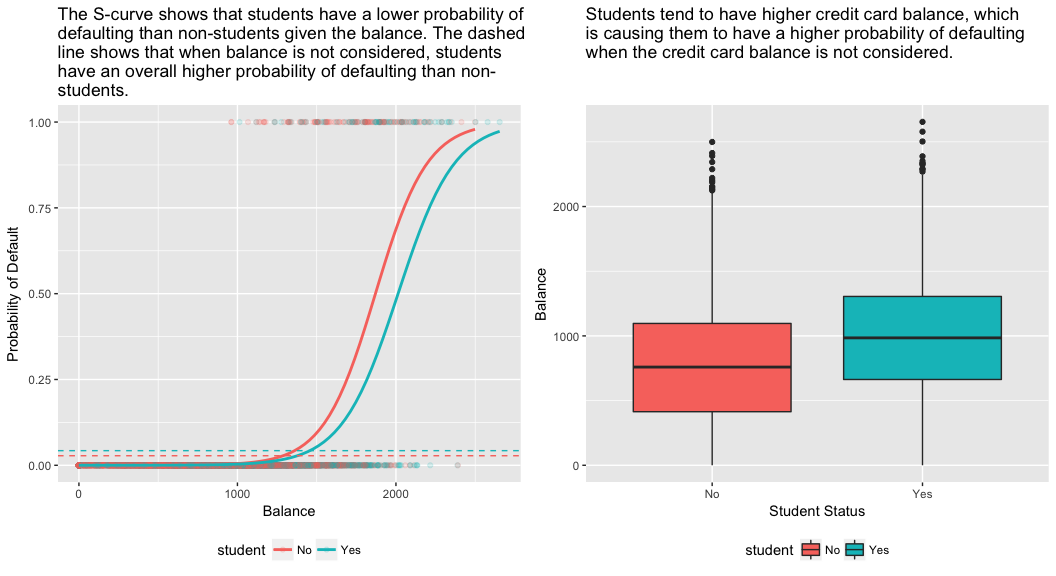
この単純な例は、他の予測因子も関連しているかもしれないときに単一の予測因子のみを含む回帰を行うことに関連する危険性と微妙な点を例示しています。 1 つの予測変数を使用して得られた結果は、特に予測変数間に相関がある場合、複数の予測変数を使用して得られた結果とはかなり異なる場合があります。 この現象は交絡として知られています。

複数の予測変数の場合、どの変数が応答（Y）変数の予測に最も影響力があるかを理解したい場合があります。 これはcaretパッケージのvarImpで行うことができます。 ここでは、バランスが最も重要で、学生のステータスはあまり重要ではなく、収入（これはとにかく重要ではないことがわかりました（p = 0.64））が続きます。

caret::varImp(model3)## Overall## balance 19.0403764## income 0.4647343## studentYes 2.5835947

以前と同様に、このモデルで簡単に予測することが可能です。 たとえば、クレジットカードの残高が 1,500 ドル、収入が 4 万ドルの学生のデフォルトの推定確率は

同じ残高と収入の非学生のデフォルトの推定確率は

new.df <- tibble(balance = 1500, income = 40, student = c("Yes", "No"))predict(model3, new.df, type = "response")## 1 2 ## 0.05437124 0.11440288

したがって、与えられた残高と収入（収入は重要ではないが）では、学生は非学生より約半分の確率でデフォルトすることがわかる。

モデルの評価&診断

ここまで、3つのロジスティック回帰モデルを構築し、その係数を検証してきました。 しかし、いくつかの重大な疑問が残っています。 そのモデルは良いものでしょうか？ モデルはどの程度データに適合しているのでしょうか。

Goodness-of-Fit

線形回帰のチュートリアルでは、F統計量、調整済み、残差診断が、モデルがデータにどれだけフィットしているかを知ることができるかを示しました。 ここでは、ロジットモデルの適合度を評価するいくつかの方法を見ていきます。

尤度比検定

最初に、私たちのモデルが適合度を向上させているかどうかを評価するために尤度比検定を使用することができます。 モデルに予測変数を追加すると、ほとんどの場合、モデルの適合が改善されますが（すなわち、対数尤度を増加させ、ヌル偏位と比較してモデルの偏位を減少させる）、モデルの適合で観察された差が統計的に有意であるかどうかを検定することが必要です。 この検定を行うにはanovaを使用します。 その結果、model1と比較して、model3は残差デビアンスを13以上減少させていることがわかります（ロジスティック回帰の目標は残差デビアンスを最小化するモデルを見つけることであることを思い出してください）。 さらに重要なことは、この改善はp=0.001で統計的に有意であることです。 これは、model3がモデル適合を改善していることを示唆しています。

anova(model1, model3, test = "Chisq")## Analysis of Deviance Table## ## Model 1: default ~ balance## Model 2: default ~ balance + income + student## Resid. Df Resid. Dev Df Deviance Pr(>Chi) ## 1 6045 908.69 ## 2 6043 895.02 2 13.668 0.001076 **## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

擬似

通常の最小二乗推定による線形回帰とは異なり、予測変数によって説明される従属変数の分散の割合を説明する統計量は存在しない。 しかし、価値があると思われる擬似的な指標は数多く存在します。 最も注目すべきはMcFaddenの で，これは

と定義される．ここで，適合モデルの対数尤度値であり，予測変数として切片だけを持つヌル・モデルの対数尤度値である． この指標は0から1弱の範囲で、0に近い値はモデルが予測力を持たないことを示す。 しかし、線形回帰とは異なり、モデルが高いMcFadden を達成することはほとんどありません。 実際、McFadden自身の言葉を借りれば、McFadden疑似のモデルは非常に良い適合を表しています。 3729>

list(model1 = pscl::pR2(model1), model2 = pscl::pR2(model2), model3 = pscl::pR2(model3))## $model1## McFadden ## 0.4726215 ## ## $model2## McFadden ## 0.004898314 ## ## $model3## McFadden ## 0.4805543

私たちのモデルのMcFaddenの擬似値を評価することができます。 しかし、モデル1と3は、デフォルトデータの分散のかなりの量を説明することを示唆する非常に高い値です。 さらに、モデル 3 は、わずかに改善するだけであることがわかります。

Residual Assessment

ロジスティック回帰は、残差が正規分布であることや分散が一定であることを仮定しないことに留意してください。 しかし、デビアンス残差は、個々のポイントがモデルによってうまく適合していないかどうかを判断するのに有用である。 ここでは、標準化されたデビアンス残差をフィットさせて、いくつが3標準偏差を超えるかを見ることができます。

model1_data <- augment(model1) %>% mutate(index = 1:n())ggplot(model1_data, aes(index, .std.resid, color = default)) + geom_point(alpha = .5) + geom_ref_line(h = 3)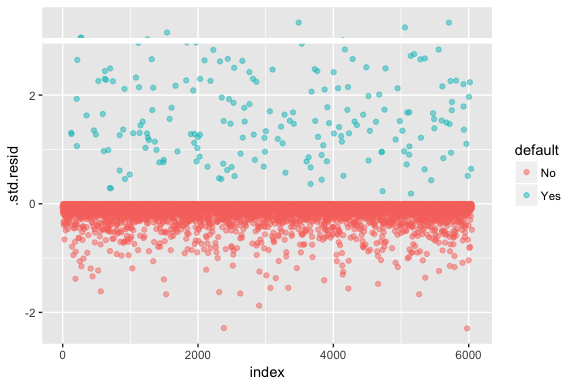

3を超えるこれらの標準化残差は、異常値の可能性を示し、より注意深い注目に値するかもしれません。 これらの残差をフィルタリングすることで、より詳しく見ることができます。

model1_data %>% filter(abs(.std.resid) > 3)## default balance .fitted .se.fit .resid .hat .sigma .cooksd .std.resid index## 1 Yes 1118.7010 -4.664566 0.1752745 3.057432 0.0002841609 0.3857438 0.01508609 3.057867 271## 2 Yes 1119.0972 -4.662320 0.1751742 3.056704 0.0002844621 0.3857448 0.01506820 3.057139 272## 3 Yes 1135.0473 -4.571902 0.1711544 3.027272 0.0002967274 0.3857832 0.01435943 3.027721 1253## 4 Yes 1066.8841 -4.958307 0.1885550 3.151288 0.0002463229 0.3856189 0.01754100 3.151676 1542## 5 Yes 961.4889 -5.555773 0.2163846 3.334556 0.0001796165 0.3853639 0.02324417 3.334855 3488## 6 Yes 1143.6805 -4.522962 0.1689933 3.011233 0.0003034789 0.3858039 0.01398491 3.011690 4142## 7 Yes 1013.2169 -5.262537 0.2026075 3.245830 0.0002105772 0.3854892 0.02032614 3.246172 5058## 8 Yes 961.7327 -5.554391 0.2163192 3.334143 0.0001797543 0.3853645 0.02322988 3.334443 5709

線形回帰と同様、我々はCookの距離値で影響力のあるオブザベーションを識別することもできる。 ここでは、上位5つの大きな値を識別します。

plot(model1, which = 4, id.n = 5)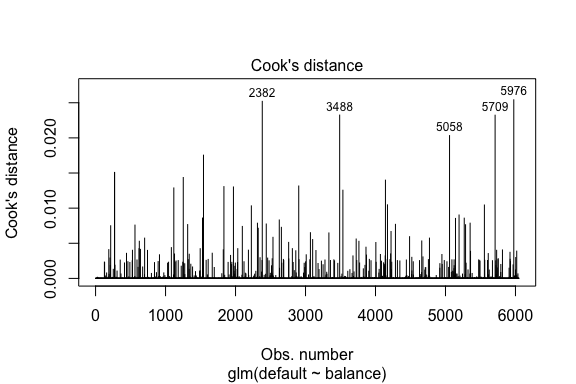

そして、我々は同様にこれらをさらに調査することができます。 ここで、影響力のある上位 5 つのポイントには、

• 非常に低い残高でデフォルトになった顧客と、
• デフォルトにならなかったが、残高が 2,000 ドル以上あった 2 人の顧客

つまり、これらの観測を削除すると、ロジスティック回帰 S カーブの形状、位置、信頼区間が変化します (推奨されません)。

model1_data %>% top_n(5, .cooksd)## default balance .fitted .se.fit .resid .hat .sigma .cooksd .std.resid index## 1 No 2388.1740 2.531843 0.2413764 -2.284011 0.0039757771 0.3866249 0.02520100 -2.288565 2382## 2 Yes 961.4889 -5.555773 0.2163846 3.334556 0.0001796165 0.3853639 0.02324417 3.334855 3488## 3 Yes 1013.2169 -5.262537 0.2026075 3.245830 0.0002105772 0.3854892 0.02032614 3.246172 5058## 4 Yes 961.7327 -5.554391 0.2163192 3.334143 0.0001797543 0.3853645 0.02322988 3.334443 5709## 5 No 2391.0077 2.547907 0.2421522 -2.290521 0.0039468742 0.3866185 0.02542145 -2.295054 5976

予測値の検証

分類率

予測のためのモデルを開発するとき、最も重要な指標は、モデルがサンプル外の観測でターゲット変数をどれだけうまく予測できるかということである。 まず、学習データセット（train）の値を予測するために、推定されたモデルを使用する必要があります。 predict を使うときは、予測がデフォルトの確率を返すように type = response を必ず入れてください。

test.predicted.m1 <- predict(model1, newdata = test, type = "response")test.predicted.m2 <- predict(model2, newdata = test, type = "response")test.predicted.m3 <- predict(model3, newdata = test, type = "response")

さて、各モデルについて、予測したターゲット変数と観測値を比較して、どちらが一番性能が良いかを見ることができます。 これはテストデータでの各モデルの分類パフォーマンスを記述する表です。 表の各象限は重要な意味を持っています。 この場合、行の中の “No “と “Yes “は、顧客がデフォルトしたかどうかを表します。 3729>

• true positive (Bottom-right quadrant): これらは、顧客がデフォルトになると予測し、実際にそうなったケースである。
• false positives (Top-right quadrant): デフォルトしないと予測したが、デフォルトしなかったケース。
• false positive (Top right quadrant): デフォルトを予測したが、実際にはデフォルトにならなかった。 (「タイプIエラー」とも呼ばれる。)
• 偽陰性(左下象限): 我々はノーと予測したが、彼らはデフォルトした。 (「第二種の過誤」ともいう。)

この結果から、model1とmodel3は非常によく似ていることがわかる。 予測されたオブザベーションの96%は真のネガティブで、約1%は真のポジティブです。 両方のモデルは、モデルが顧客がデフォルトしないと予測したが、実際にはデフォルトしてしまったという3%未満の第2種の過誤を持ちます。 そして、両方のモデルは、モデルが顧客がデフォルトすると予測するが、実際にはデフォルトしなかった場合の1%未満のタイプIエラーを持っています。 model2 の結果は著しく異なっています。このモデルは、デフォルトしない人を正確に予測しますが（データの 97% がデフォルトしない人である結果）、デフォルトする顧客を実際には予測しません！

list( model1 = table(test$default, test.predicted.m1 > 0.5) %>% prop.table() %>% round(3), model2 = table(test$default, test.predicted.m2 > 0.5) %>% prop.table() %>% round(3), model3 = table(test$default, test.predicted.m3 > 0.5) %>% prop.table() %>% round(3))## $model1## ## FALSE TRUE## No 0.962 0.003## Yes 0.025 0.010## ## $model2## ## FALSE## No 0.965## Yes 0.035## ## $model3## ## FALSE TRUE## No 0.963 0.003## Yes 0.026 0.009

私たちは、誤分類（別名エラー）率（あるいはこれを正確率に置き換えることもできます）を理解したいのです。 モデル 1 とモデル 3 の間にあまり改善は見られず、モデル 2 は低いエラー率ですが、実際にデフォルトになる顧客を正確に予測することはないことを忘れないでください。 モデル1を見て、説明しましょう。 デフォルトになった顧客の合計があることがわかります。 全体のデフォルトのうち、予測されなかったものがあります。 あるいは、デフォルトの発生のみが予測されたと言うこともできます。これは、モデルの精度（感度としても知られています）として知られています。 つまり、全体のエラー率が低い一方で、精度も低く、良いとは言えません！

table(test$default, test.predicted.m1 > 0.5)## ## FALSE TRUE## No 3803 12## Yes 98 40

分類モデルでは、モデルのパフォーマンスを特徴付けるときに、感度と特異度という用語も出てきます。 前述のように、感度は精度と同義です。 しかし、特異度は、ここでは、正しく識別された非貸倒者のパーセンテージです（ここでの精度は、我々のデータ中のオブザベーションの97%が非貸倒者であるという事実によって大きく左右されています）。 sensititivyとspecificityの間の重要性は文脈に依存します。 この場合、クレジットカード会社はリスクを減らしたいので、sensititivyをより重視する可能性が高いです。

受信動作特性（ROC）は、分類器の性能の視覚的な尺度です。 正しく正とみなされる正のデータ点の割合と、誤って正とみなされる負のデータ点の割合を用いて、何かを正しく予測できる割合と何かを誤って予測する割合との間のトレードオフを示すグラフィックを生成するのです。 最終的には、ROC曲線の下での面積、つまりAUCに注目する。 この指標は0.50から1.00の範囲で、0.80以上の値は、ターゲット変数を構成する2つのカテゴリの間でモデルがよく識別することを示します。 モデル1とモデル2のROCとAUCを比較すると、性能に強い差があることがわかります。 我々は、ROCプロットがモデル2（右）ではなく、モデル1（左）のようになることを強く望んでいます！

library(ROCR)par(mfrow=c(1, 2))prediction(test.predicted.m1, test$default) %>% performance(measure = "tpr", x.measure = "fpr") %>% plot()prediction(test.predicted.m2, test$default) %>% performance(measure = "tpr", x.measure = "fpr") %>% plot()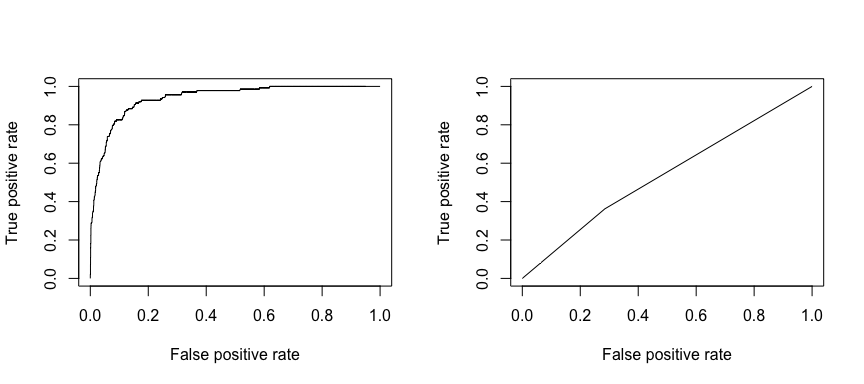

そしてAUCを数値的に計算するには、以下を使用することができます。 AUCは0.50～1.00の範囲になることを覚えておいてください。 したがって、モデル 2 は非常に悪い分類モデルである一方、モデル 1 は非常に良い分類モデルです。

# model 1 AUCprediction(test.predicted.m1, test$default) %>% performance(measure = "auc") %>% [email protected]## ]## 0.939932# model 2 AUCprediction(test.predicted.m2, test$default) %>% performance(measure = "auc") %>% [email protected]## ]## 0.5386955

これらの分類率を改善するために、モデルを「調整」し続けることができるのです。 AUC と ROC カーブを向上させることができれば (これは分類精度率を向上させていることを意味します)、「リフト」を作成している、つまり、分類精度を引き上げていることになります。

Additional Resources

これにより、ロジスティック回帰を使いこなすことができます。 もっと掘り下げることができることがたくさんあるので、以下のリソースはもっと学ぶのに役立ちます。

• An Introduction to Statistical Learning
• Applied Predictive Modeling
• Elements of Statistical Learning