Números primos y números compuestos

En el post de hoy, aprenderás la diferencia entre números primos y compuestos. Además, te mostraremos varios ejemplos para que los entiendas mejor.

¿Qué son los números primos?

Los números primos son los números que sólo son divisibles por sí mismos y por el 1, es decir, si intentamos dividirlos por otro número, el resultado no es un número entero. Por lo tanto, si dividimos el número entre cualquier cosa que no sea el uno o él mismo, obtendremos un resto que no es cero.

Números primos hasta el 100

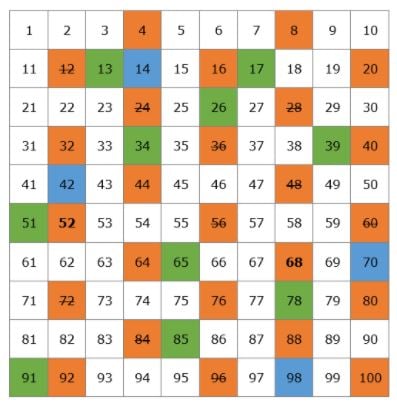
Vamos a crear una tabla con todos los números primos que existen hasta el 100.

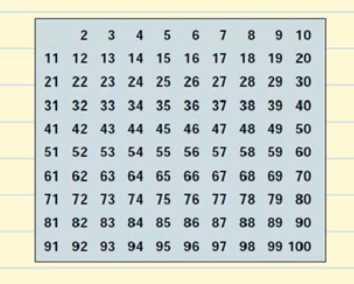
Empecemos por el 2. El 2 es un número primo pero todos los múltiplos de 2 serán números compuestos ya que serán divisibles por 2. Tachamos todos los múltiplos de 2 en la tabla.

El siguiente número primo es el 3, así que podemos tachar todos los múltiplos de 3 ya que serán números compuestos.

Después del 3, está el siguiente número primo, el 5, así que tachamos todos los múltiplos del 5.

Luego tenemos el número primo 7 y tachamos todos los múltiplos del 7.

El siguiente número primo es el 11, así que tachamos todos los múltiplos del 11 que son el 22, 33, 44, 55, 66, 77, 88 y 99. Todos estos números ya habían sido tachados así que hemos terminado de tachar todos los números compuestos de nuestra tabla.

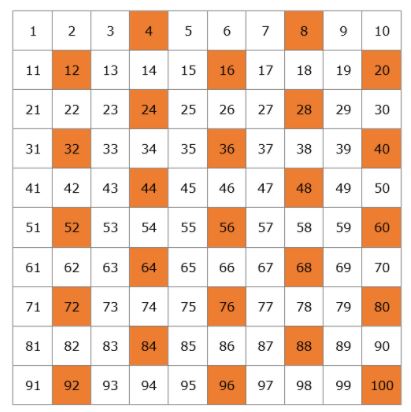
Esta es nuestra lista de números primos del 1 al 100. No tienes que memorizarlos pero sería mejor que recordaras los números más pequeños, como el 2, 3, 5, 7, 11, 13.

¿Cuántos números primos hay?

El matemático griego Eratóstenes (siglo III a.C.) diseñó una forma rápida de encontrar todos los números primos hasta un número determinado. Es un proceso llamado la Criba de Eratóstenes.

Nota que entre 1 y 100 hay 25 números primos. ¿Cuántos números primos hay en total? Desde la antigüedad sabemos que hay una cantidad infinita, por lo que es imposible enumerarlos todos. Como Euclides, que fue el primero en demostrar que había una cantidad infinita en el siglo IV a.C., no conocía el concepto de infinito dijo que «los números primos son más que cualquier multitud fija de ellos», lo que significa que si imaginas 100, hay más, y si imaginas un millón todavía hay más.

Números primos del 100 al 1.000

Veamos los números primos del 100 al 1.000.

Sentimos no poder mostrarlos todos, como sabes hay una cantidad infinita. 😉

Ejemplos de números primos

Para ayudarte a entender mejor los números primos, vamos a explicar un ejercicio.

Sara tiene 6 caramelos que quiere compartir, pero no sabe con cuántas personas puede compartirlos para que todos reciban la misma cantidad y no sobre ninguno. ¿De cuántas maneras puede hacerlo?

Aquí está Sara y sus 6 caramelos:

¿Cómo podemos dividirlos?

La primera y más fácil manera es dárselos a una sola persona, es decir, dividirlos por 1. De esta manera esa persona tendrá 6 caramelos.

La siguiente posibilidad es dividirlos entre 2 personas. Como 6 dividido entre 2 es 3, ¡cada persona recibe 3 caramelos!

Vamos a continuar con el siguiente número, el 3. Si dividimos 6 caramelos entre 3 personas también es una división exacta y cada persona recibirá 2 caramelos:

Continuemos con los números. No tenemos divisiones exactas con el 4 y el 5, pero sí con el 6.

Como 6 dividido entre 6 es 1, podemos dar a 6 niños 1 caramelo a cada uno.

Vamos a recoger algo de información. Tenemos 6 caramelos que podemos repartir (con una división exacta) entre 1, 2, 3 y 6 personas. Es decir, podemos dividir el número 6 y obtener 0 como resto al dividirlo entre 1, 2, 3 y 6. Estos números se conocen como los divisores del 6.

Vamos a probar con otro número, el 7 por ejemplo.

Ahora Sara tiene 7 caramelos y quiere repartirlos, pero no sabe con cuántas personas puede repartirlos para que todos reciban la misma cantidad y no sobre ninguno. ¿De cuántas maneras puede hacerlo?

¡Henry tiene mucha suerte! Le han tocado todos los caramelos!

¿Hay otras formas de hacerlo? No podemos dividir 7 entre 2, 3, 4, 5 o 6, …¡pero 7 es posible!

Sara puede repartir los caramelos entre 7 personas, dándoles un caramelo a cada una:

Así que 7 sólo se puede dividir entre 1 y 7, sus únicos divisores son 1 y 7. Estos son los tipos de números que llamamos números primos.

¿Hay más números primos? Por supuesto. Busquemos algunos más:

• ¿Es el 4? No. Porque sus divisores son 1, 2 y 4.
• ¿Es el 5? Sí. Porque sus divisores son 1 y 5.
• ¿Es 8? No. Porque sus divisores son 1, 2, 4 y 8.

En resumen, un número es primo si sólo tiene 2 divisores: 1 y él mismo.

¡Ahora puedes buscar muchos números primos!

Cómo encontrar números primos

¡Pon mucha atención! Vamos a darte un truco para saber si un número es primo o no, sin tener que buscar sus divisores, pero de una forma más divertida y que nos da los divisores (si los tienen).

Elegimos un número al azar, el 16 por ejemplo.

Para comprobar si es un número primo o no, vamos a utilizar una tabla muy parecida a las tarjetas Montessori para multiplicar. Y obtendremos tantas bolas como el número que hayamos elegido. En este caso, 16 bolas.

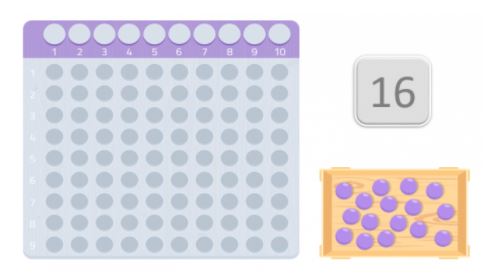
Una vez que tengamos la tabla y las bolas, debemos colocarlas sobre la mesa empezando por el primer espacio, intentando formar un rectángulo. Los números que forman los bordes del rectángulo son los divisores de ese número.

En caso de que sólo consigamos formar un rectángulo con el mismo número que estamos utilizando y el número 1, será un número primo.

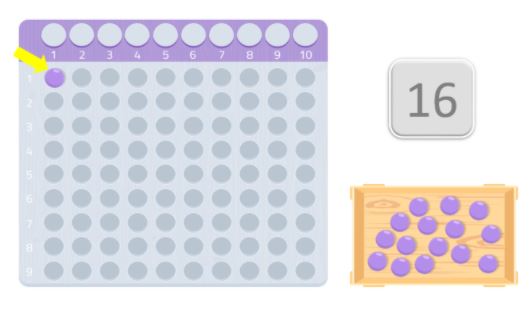
Por ejemplo, en este caso, colocamos 8 bolas en la primera fila y 8 más en la segunda. Como puedes ver, hemos formado un rectángulo y podemos ver que 8, como 2, son divisores del número 16. Por tanto, el 16 no es un número primo porque, como sabes, los números primos son aquellos que sólo son divisibles por sí mismos y por 1.

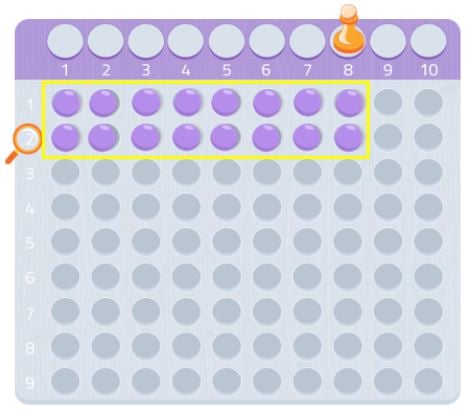
Podemos probar con otro número, el 7 por ejemplo.

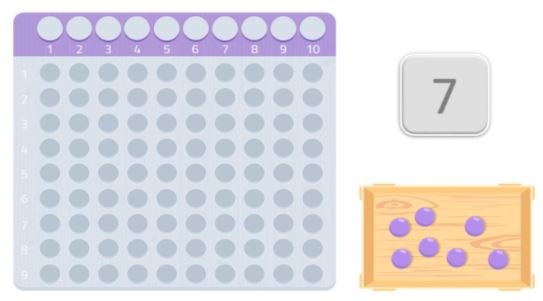
Como vemos, no podríamos hacer un rectángulo completo, nos faltaría una bola. Como no podemos formar un rectángulo, podríamos decir que el número 7 no tiene más divisores que él mismo y el 1, como podemos ver en la siguiente imagen.

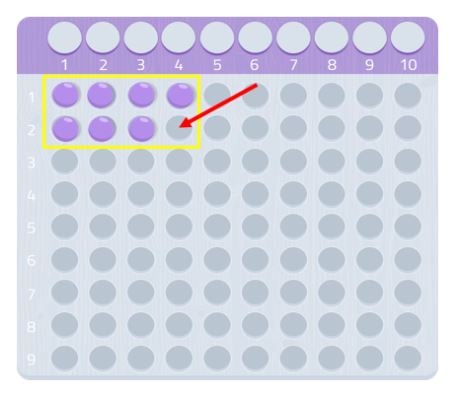
Por lo tanto, ¡el 7 es un número primo!

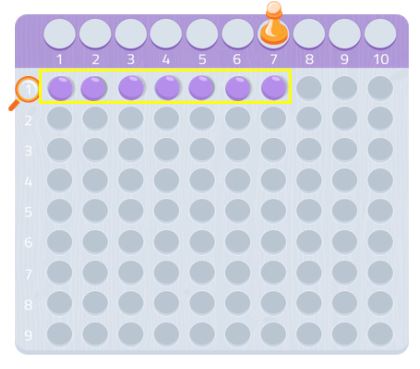
Prueba con cualquier otro número, ¡ya verás cómo funciona! Puedes usar papel cuadriculado y buscar rectángulos usando ese número de cuadrados.

¿Por qué son importantes los números primos?

Los números primos son la clave de la aritmética, a continuación verás un ejemplo que demuestra su importancia, no sólo en las matemáticas sino también en la naturaleza.

¿Qué queremos decir cuando decimos que los números primos son la clave de la aritmética?

Esto se debe a que cualquier número consiste en un producto único formado por una serie de estos números.

Se cree que se estudian desde hace unos 20.000 años, cuando un antepasado nuestro anotó una serie de números primos (11, 13, 17 y 19) en el hueso de Ishango. Por si fuera una casualidad, se ha confirmado que los antiguos egipcios trabajaban con ellos hace 4.000 años.

Además, la naturaleza los conoce muy bien y algunas especies han sabido descubrirlos a lo largo de su evolución y aprovecharlos para sobrevivir.

Me refiero a varias especies de cigarras, como la Magicicada septendecium que vive en Norteamérica. Esta especie de cigarra tiene establecido su ciclo de reproducción en torno a los 13 o 17 años, no 12, 14, 15, 16 o 18, exactamente 13 o 17. Esto les permite evitar a los depredadores que también tienen ciclos reproductivos periódicos; imaginemos un depredador con un ciclo reproductivo de 4 años.

Si el ciclo vital de una cigarra fuera de 12 o 14 años, coincidiría con un depredador con mucha frecuencia, mucho más que si fuera de 13 o 17 años. Exactamente 2 veces cada 100 años, mientras que en caso contrario, coincidirían en 11 ciclos lo que comprometería el desarrollo de la especie.

La seguridad de las comunicaciones electrónicas se basa también en los números primos. Cada mensaje encriptado que se envía por Internet (redes de mensajes, compras o banca electrónica) lleva asociado un número primo, y es muy difícil saber si es primo o no. El receptor tiene uno de sus divisores, y por eso puede desencriptarlo. Así que tener números primos es fundamental para nuestra privacidad cuando nos comunicamos electrónicamente.

¿Qué son los números compuestos?

Los números compuestos son aquellos números que son divisibles por 1 y por ellos mismos, así como por otros números.

Vamos a ver un ejemplo de número primo y de número compuesto.

El 11 se puede escribir como la multiplicación 1 x 11, pero no se puede escribir como ninguna otra multiplicación de números naturales. Sólo tiene los divisores 1 y 11, y por lo tanto es un número primo.

12 se puede escribir como la multiplicación 1 x 12 y como la multiplicación 3 x 4, y 2 x 6. Como 12 es divisible por más números que el 1 y por sí mismo, 12 es un número compuesto.

¿Es el 1 un número primo?

Hay gente que lo cree así porque dice que el 1 sólo puede ser dividido por 1 y por sí mismo pero en matemáticas, el número 1 ha sido descartado como número primo porque sólo tiene un divisor. De hecho, el criterio de «un entero positivo es primo si tiene exactamente dos divisores positivos» se utiliza para excluir el número uno de la lista de números primos. No es porque seamos quisquillosos con él, sino que si el número uno se considerara primo habría que decir muchas propiedades matemáticas de forma diferente.

¿Entonces, el 1 es un número compuesto?

Pues tampoco es compuesto ya que no se puede poner como producto de números primos. El número 1 no es primo ni compuesto. Y antes de que lo preguntes, el cero tampoco es primo ni compuesto pero esto se debe a todas las consideraciones que estábamos explicando para los números positivos, es decir, mayores que el cero.

Divisores de un número

El divisor de un número es el valor que divide al número en partes exactas, es decir, tiene un resto de 0.

Como ejemplo, vamos a calcular los divisores de 24.

Empezamos a dividir con los números más pequeños empezando por el 1.

• 24 / 1 = 24. Tanto 1 como 24 son divisores.
• 24 / 2 = 12. Así que 2 y 12 son divisores.
• 24 / 3 = 8. Así que 3 y 8 son divisores.
• 24 / 4 = 6. Así que 4 y 6 son divisores.
• 24 / 5 = 4. No es una división exacta y tiene un resto de 4 por lo que 5 no es un divisor.

El siguiente número es el 6, pero como ya sabemos que el 6 es un divisor de 24 hemos terminado de calcular los divisores de 24.

Vídeo: Factorización y números primos

Si quieres saber más sobre números primos y compuestos, echa un vistazo al siguiente vídeo. También aprenderás el concepto de factorización utilizando la tabla Montessori.

Este vídeo es uno de nuestros tutoriales interactivos y, aunque no es interactivo, puedes verlo tantas veces como necesites y compartirlo con tus amigos. Si quieres acceder a nuestros tutoriales interactivos, ¡regístrate en Smartick! El método online para ayudar a los niños de 4 a 14 años a aprender y practicar las matemáticas.

Si quieres seguir aprendiendo sobre los números primos y las mejores matemáticas adaptadas a tu nivel, ¡regístrate en Smartick y pruébalo gratis!

Aprende más:

• Números primos y números compuestos
• Números primos: Un truco para ayudarte a identificarlos
• Números primos: Cómo encontrarlos con la criba de Eratóstenes
• Aprende a factorizar en números primos
• Actividades con números primos con Smartick

• Autor
• Puestos recientes

Equipo de creación de contenidos.
¡Un equipo multidisciplinar y multicultural formado por matemáticos, maestros, profesores y otros profesionales de la educación!
Se esfuerzan por crear el mejor contenido matemático posible.