ΔS berekenen uit thermodynamische cycli
We kunnen een verandering in entropie ook berekenen met behulp van een thermodynamische cyclus. Zoals u eerder hebt geleerd, is de molaire warmtecapaciteit (Cp) de hoeveelheid warmte die nodig is om de temperatuur van 1 mol van een stof met 1°C te doen stijgen bij constante druk. Op dezelfde manier is Cv de hoeveelheid warmte die nodig is om de temperatuur van 1 mol van een stof met 1°C te laten stijgen bij een constant volume. De toename van de entropie bij toenemende temperatuur in figuur is ongeveer evenredig met de warmtecapaciteit van de stof.
Houd in gedachten dat de entropieverandering (ΔS) gerelateerd is aan de warmtestroom (qrev) door ΔS = qrev/T. Omdat qrev = nCpΔT bij constante druk of nCvΔT bij constant volume, waarbij n het aantal mol van de aanwezige stof is, is de verandering in entropie voor een stof waarvan de temperatuur verandert van T1 in T2 als volgt:
Zoals je zult ontdekken in meer gevorderde wiskundecursussen dan hier vereist is, kan worden aangetoond dat dit gelijk is aan het volgende:Voor een overzicht van natuurlijke logaritmen, zie Essentiële vaardigheden 6 in hoofdstuk 11 “Vloeistoffen”.
Zo kunnen we een combinatie gebruiken van warmtecapaciteitsmetingen (Vergelijking 18.20 of Vergelijking 18.21) en experimenteel gemeten waarden van enthalpie’s van fusie of verdamping als er sprake is van een faseverandering (Vergelijking 18.18) om de entropieverandering te berekenen die overeenkomt met een verandering in de temperatuur van een monster.
We kunnen een thermodynamische cyclus gebruiken om de entropieverandering te berekenen als de faseverandering voor een stof als zwavel niet rechtstreeks kan worden gemeten. Zoals in de oefening in voorbeeld 6 is opgemerkt, bestaat elementair zwavel in twee vormen (deel (a) in figuur): een orthorhombische vorm met een sterk geordende structuur (Sα) en een minder geordende monokliene vorm (Sβ). De orthorhombische (α) vorm is stabieler bij kamertemperatuur maar ondergaat een faseovergang naar de monokliene (β) vorm bij temperaturen hoger dan 95,3 °C (368,5 K). De overgang van Sα naar Sβ kan worden beschreven door de thermodynamische cyclus die in deel (b) van figuur is weergegeven en waarin vloeibare zwavel een tussenproduct is. De verandering in entropie die gepaard gaat met de omzetting van vloeibare zwavel in Sβ (-ΔSfus(β) = ΔS3 in de cyclus) kan niet rechtstreeks worden gemeten. Omdat entropie een toestandsfunctie is, kan ΔS3 echter worden berekend uit de totale entropieverandering (ΔSt) voor de Sβ-Sβ-overgang, die gelijk is aan de som van de ΔS-waarden voor de stappen in de thermodynamische cyclus, met behulp van vergelijking 18. ΔS3 kan worden berekend uit de totale entropieverandering (ΔSt) voor de Sβ-Sβ-overgang, die gelijk is aan de som van de ΔS-waarden voor de stappen in de thermodynamische cyclus.20 en de getabelleerde thermodynamische parameters (de warmtecapaciteiten van Sα en Sβ, ΔHfus(α), en het smeltpunt van Sα.)

Oplossing voor ΔS3 levert een waarde van -3,24 J/(mol-K) op. Zoals verwacht voor de omzetting van een minder geordende toestand (een vloeistof) in een meer geordende (een kristal), is ΔS3 negatief.
Hoe worden entropieën gemeten
De absolute entropie van een stof bij elke temperatuur boven 0 K moet worden bepaald door de toename van warmte q te berekenen die nodig is om de stof van 0 K tot de gewenste temperatuur te brengen, en vervolgens de verhoudingen q/T bij elkaar op te tellen. Er zijn twee soorten experimentele metingen nodig:
- De enthalpie’s verbonden met alle faseveranderingen die de stof kan ondergaan binnen het temperatuurbereik van belang. Het smelten van een vaste stof en het verdampen van een vloeistof komen overeen met een aanzienlijke toename van het aantal microstaten dat beschikbaar is om thermische energie op te nemen, zodat, wanneer deze processen plaatsvinden, energie in een systeem zal stromen en deze nieuwe microstaten zal vullen in de mate die nodig is om een constante temperatuur te handhaven (het vries- of kookpunt); deze instromen van thermische energie komen overeen met de smelt- en verdampingswarmte. De entropietoename bij het smelten bijvoorbeeld bedraagt slechts ΔHfusie/Tm.
- De warmtecapaciteit C van een fase drukt de hoeveelheid warmte uit die nodig is om de temperatuur met een kleine hoeveelheid ΔT , of preciezer, met een infinitesimale hoeveelheid dT , te veranderen. De entropietoename die veroorzaakt wordt door de opwarming van een stof over een temperatuurbereik dat geen faseovergang omvat, wordt dus gegeven door de som van de hoeveelheden C dT/T voor elke toename van de temperatuur dT . Dit is natuurlijk gewoon de integraal
Omdat de warmtecapaciteit zelf enigszins temperatuurafhankelijk is, moet voor de nauwkeurigste bepalingen van absolute entropieën in bovenstaande integraal de functionele afhankelijkheid van C van T worden gebruikt in plaats van een constante C.
Wanneer dit niet bekend is, kan men een reeks warmtecapaciteitsmetingen over smalle temperatuurstappen ΔT uitvoeren en het oppervlak onder elk deel van de kromme meten.
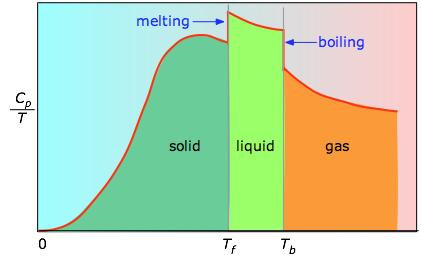
Het oppervlak onder elk deel van de kromme geeft de entropieverandering weer die optreedt bij verwarming van de stof over een interval ΔT. Hieraan moeten de enthalpie van smelten, verdampen en van elke vaste stof/vaste faseverandering worden toegevoegd. Waarden van Cp voor temperaturen nabij nul worden niet rechtstreeks gemeten, maar kunnen worden geschat op grond van de kwantumtheorie.
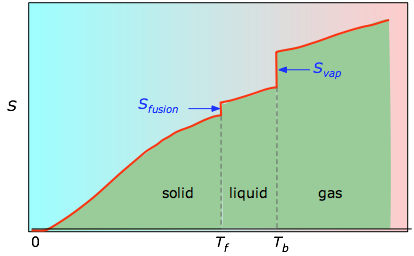
De cumulatieve oppervlakten van 0 K tot een gegeven temperatuur (ontleend aan de experimentele grafiek links) worden vervolgens uitgezet als functie van T, en eventuele entropieën van faseveranderingen zoals Svap = Hvap / Tb worden opgeteld om de absolute entropie bij temperatuur T te verkrijgen.