Factorials kom je overal in de combinatoriek tegen, omdat ze daar vandaan komen. De factorial werd gecreëerd als een manier om het aantal regelingen van een groep items uit te drukken, die we natuurlijk vinden door, in zijn meest elementaire vorm, de vermenigvuldigingsregel van het tellen te gebruiken.
De factorial is een soort van de officieuze bewerking van de vermenigvuldigingsregel van het tellen.
Waarom nul factorial gelijk is aan 1
Dit is waar het lastig wordt, want als we alleen denken aan factorials in de context waarin ze gewoonlijk worden gedefinieerd, d. w. z.d.w.z. het “product van alle positieve gehele getallen kleiner dan of gelijk aan het getal”, dan is het uitzoeken van 0! als tegen een stenen muur aanlopen.
De meeste mensen zullen je vertellen dat 0! gedefinieerd is als 1, en als je vraagt waarom zeggen ze gewoon “omdat het gedefinieerd is als 1”.
Ja, dat is behoorlijk frustrerend. Het is het wiskundige equivalent van aan je ouders vragen waarom je een willekeurige regel van hen moet volgen en dan te horen krijgen: “Omdat ik het zeg.”
Hoewel dat een geaccepteerde opvoedtechniek is, is het een waardeloze manier om wiskunde te leren. Dus wat is de deal? Hoe hebben we besloten dat nul factorie gelijk is aan één?
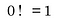
Een intuïtief begrip
Herken je nog dat we zeiden dat de factorie zijn oorsprong vindt in de wiskundige bewerking van het vinden van het aantal permutaties of rangschikkingen van een verzameling? (Let op: niet de permutaties van een kleinere set uit een grotere set, maar gewoon de rangschikkingen van een gegeven set.)
Nul factorie kan worden gezien als het aantal rangschikkingen van nul elementen in een set, aka de lege set {}. (Als je ooit sets hebt bestudeerd, misschien in basisstatistiek of discrete wiskunde, ben je waarschijnlijk bekend met het concept van de lege set. Het is letterlijk de verzameling van niets.)
Als ik je nu zou vragen hoeveel schikkingen er zijn van één ding, dan zou je 1 antwoorden, omdat er maar één manier is om één ding te schikken. Hetzelfde idee volgt hier. Ons “ene ding” is de lege verzameling, en het aantal schikkingen van de lege verzameling is één. Dat is het. Daarom is 0 gelijk aan 1.
Hoe vereenvoudig je factoriële uitdrukkingen
Nu we de basisbeginselen achter de rug hebben, is het tijd voor het hart van onze factorie-tutorial: vereenvoudigen.
De beste manier om wiskunde te zien is in actie. Dus hier ben ik om je door de zes problemen te leiden die in de afbeelding bovenaan dit bericht staan! We beginnen lekker makkelijk, gaan dan naar de combinatieformule met getallen en variabelen, en eindigen met wat lastiger factoriale uitdrukkingen.
❤ STAY CONNECTED ❤
Niets te missen, of een wiskundeprobleem!