In het bericht van vandaag leert u het verschil tussen priemgetallen en samengestelde getallen. Bovendien zullen we u verschillende voorbeelden tonen om u te helpen ze beter te begrijpen.
Index
Wat zijn priemgetallen?
Prime getallen zijn de getallen die alleen deelbaar zijn door zichzelf en 1, met andere woorden, als we ze proberen te delen door een ander getal, is de uitkomst geen geheel getal. Dus, als je het getal deelt door iets anders dan één of zichzelf, dan krijg je een rest die niet nul is.
Priemgetallen tot 100
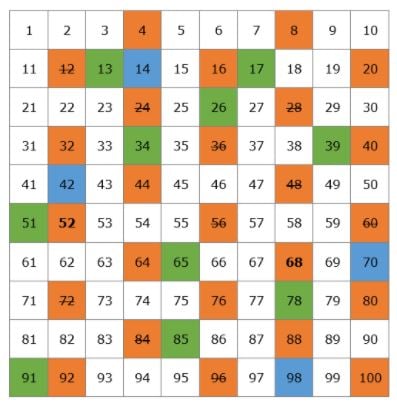
We gaan een tabel maken met alle priemgetallen die bestaan tot 100.
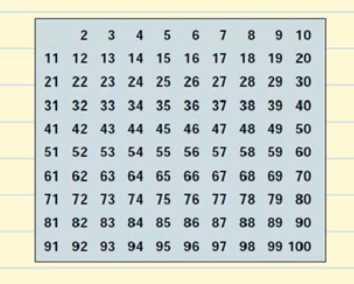
Laten we beginnen met 2. 2 is een priemgetal, maar alle veelvouden van 2 zijn samengestelde getallen, omdat ze deelbaar zijn door 2. We schrappen alle veelvouden van 2 in de tabel.
Het volgende priemgetal is 3, dus we kunnen alle veelvouden van 3 schrappen, omdat het samengestelde getallen zijn.
Na 3 komt het volgende priemgetal 5, dus we strepen alle veelvouden van 5 door.
Dan hebben we het priemgetal 7 en we strepen alle veelvouden van 7 door.
Het volgende priemgetal is 11, dus we strepen alle veelvouden van 11 door, dat zijn 22, 33, 44, 55, 66, 77, 88, en 99. Al deze getallen waren al doorgestreept, dus we zijn nu klaar met het doorstrepen van alle samengestelde getallen op onze tabel.

Dit is onze lijst van priemgetallen van 1 tot 100. Je hoeft ze niet uit je hoofd te leren, maar het zou het beste zijn als je de kleinere getallen onthoudt, zoals 2, 3, 5, 7, 11, 13.
Hoeveel priemgetallen zijn er?
De Griekse wiskundige Eratosthenes (3e eeuw v. Chr.) ontwierp een snelle manier om alle priemgetallen tot een bepaald getal te vinden. Het is een proces dat de Zeef van Eratosthenes wordt genoemd.
Merk op dat er tussen 1 en 100 25 priemgetallen zijn. Hoeveel priemgetallen zijn er in totaal? We weten al sinds de oudheid dat er oneindig veel zijn, dus het is onmogelijk om ze allemaal op te sommen. Aangezien Euclides, die in de 4de eeuw voor Christus als eerste aantoonde dat er oneindig veel waren, het begrip oneindigheid niet kende, zei hij “priemgetallen zijn meer dan een vaste veelheid ervan”, wat betekent dat als u zich 100 voorstelt, er meer zijn, en als u zich een miljoen voorstelt, zijn er nog meer.
Priemgetallen 100 tot 1.000
Laten we eens kijken naar de priemgetallen van 100 tot 1.000.

Het spijt ons dat we ze niet allemaal kunnen laten zien, zoals u weet zijn er oneindig veel. 😉
Priemgetallen Voorbeelden
Om u te helpen priemgetallen beter te begrijpen, gaan we een oefening uitleggen.
Sara heeft 6 snoepjes die ze wil delen, maar ze weet niet met hoeveel mensen ze ze kan delen, zodat iedereen evenveel krijgt en er geen overblijft. Op hoeveel manieren kan ze dit doen?
Hier is Sara met haar 6 snoepjes:

Hoe kunnen we ze verdelen?
De eerste en makkelijkste manier is om ze aan 1 persoon te geven, met andere woorden, delen door 1. Op die manier krijgt die persoon 6 snoepjes.
De volgende mogelijkheid is om ze te verdelen over 2 personen. Aangezien 6 gedeeld door 2 3 is, krijgt elke persoon 3 snoepjes!

We gaan verder met het volgende getal, 3. Als we 6 snoepjes verdelen over 3 personen is dat ook een exacte deling en krijgt elke persoon 2 snoepjes:

Laten we verder gaan met de getallen. Bij 4 en 5 hebben we geen exacte deling, maar bij 6 wel.
Omdat 6 gedeeld door 6 1 is, kunnen we 6 kinderen elk 1 snoepje geven.

We gaan nu wat informatie verzamelen. We hebben 6 snoepjes die we (met een exacte verdeling) kunnen verdelen onder 1, 2, 3, en 6 personen. Met andere woorden, we kunnen het getal 6 delen en krijgen 0 als rest als we het delen door 1, 2, 3, en 6. Deze getallen staan bekend als de delers van 6.
We gaan het nu proberen met een ander getal, 7 bijvoorbeeld.
Nu heeft Sara 7 snoepjes en wil ze delen, maar ze weet niet met hoeveel mensen ze kan delen zodat iedereen evenveel krijgt en er geen overblijft. Op hoeveel manieren kan ze dit doen?

Henry heeft zo’n geluk! Hij heeft alle snoepjes!
Zijn er nog andere manieren? We kunnen 7 niet delen door 2, 3, 4, 5 of 6, … maar 7 kan wel!
Sara kan de snoepjes verdelen onder 7 mensen, door ze elk een snoepje te geven:

Dus 7 kan alleen gedeeld worden door 1 en 7, de enige delers zijn 1 en 7. Dit zijn de getallen die we priemgetallen noemen.
Zijn er nog meer priemgetallen? Natuurlijk! Laten we er nog een paar zoeken:
- Is 4? Nee! Want zijn delers zijn 1, 2 en 4.
- Is 5? Ja! Omdat de delers 1 en 5 zijn.
- Is 8? Nee! Omdat zijn delers 1, 2, 4 en 8 zijn.
In het kort, een getal is priem als het slechts 2 delers heeft: 1 en zichzelf.
Nu kun je veel priemgetallen zoeken!
Hoe priemgetallen vinden
Let goed op! We gaan je een trucje geven om te weten of een getal priem is of niet, zonder dat je naar de delers hoeft te zoeken, maar op een manier die leuker is en ons de delers geeft (als ze die hebben).
Laten we een willekeurig getal kiezen, 16 bijvoorbeeld.
Om te kijken of het een priemgetal is of niet, gaan we een tabel gebruiken die erg lijkt op Montessori-kaarten om te vermenigvuldigen. En we krijgen evenveel ballen als het getal dat we hebben gekozen. In dit geval 16 ballen.
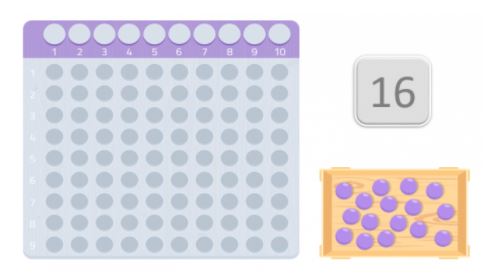
Als we de tafel en de ballen hebben, moeten we ze op de tafel leggen, beginnend met het eerste hokje, en proberen een rechthoek te vormen. De getallen die de randen van de rechthoek vormen, zijn de delers van dat getal.
In het geval dat we er alleen in slagen een rechthoek te vormen met hetzelfde getal dat we gebruiken en het getal 1, zal het een priemgetal zijn.
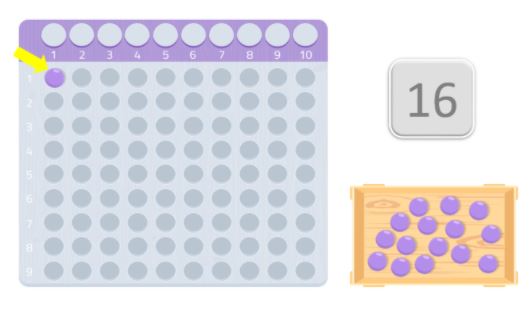
In dit geval bijvoorbeeld, plaatsen we 8 ballen in de eerste rij en nog eens 8 in de tweede. Zoals u ziet, hebben we een rechthoek gevormd en zien we dat 8, net als 2, delers zijn van het getal 16. Daarom is 16 geen priemgetal, want zoals je weet zijn priemgetallen getallen die alleen deelbaar zijn door zichzelf en 1.
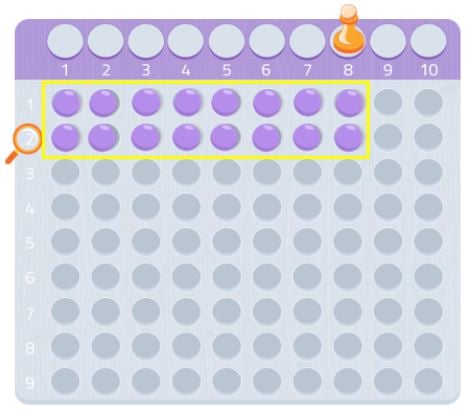
We kunnen het ook met een ander getal proberen, 7 bijvoorbeeld.
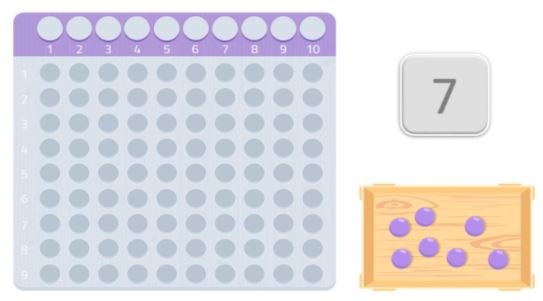
Zoals we kunnen zien, kunnen we geen volledige rechthoek maken, we zouden een bal missen. Omdat we geen rechthoek kunnen vormen, kunnen we zeggen dat het getal 7 geen andere delers heeft dan zichzelf en 1, zoals we in de volgende afbeelding kunnen zien.
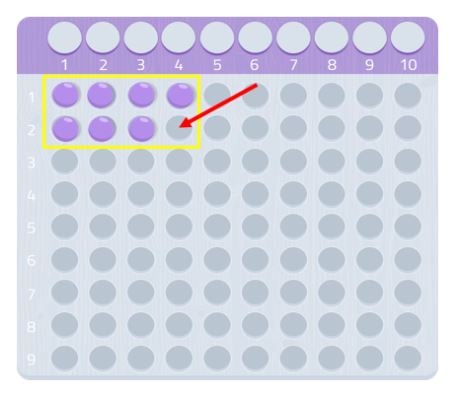
Daarom is 7 een priemgetal!
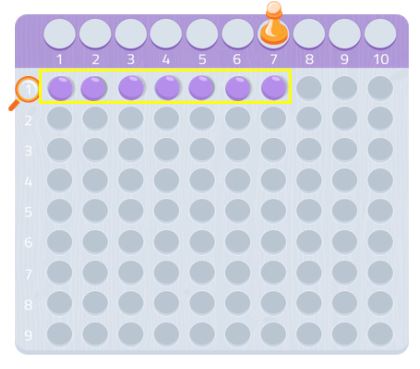
Probeer maar eens een ander getal, je zult zien hoe het werkt! Je kunt grafiekpapier gebruiken en rechthoeken zoeken met dat aantal vierkanten.
Waarom zijn priemgetallen belangrijk?
Prime numbers are the key to arithmetic, hieronder zie je een voorbeeld dat hun belang aantoont, niet alleen in de wiskunde maar ook in de natuur.
Wat bedoelen we als we zeggen dat priemgetallen de sleutel tot de rekenkunde zijn?
Dat komt omdat elk getal bestaat uit een uniek product dat bestaat uit een reeks van deze getallen.
Men gelooft dat ze al zo’n 20.000 jaar bestudeerd worden, toen een voorouder van ons een reeks priemgetallen (11, 13, 17 en 19) opschreef op het Ishango-botje. Alsof dit toeval was, is bevestigd dat de oude Egyptenaren er 4000 jaar geleden al mee werkten.
Daar komt bij dat de natuur ze heel goed kent en dat sommige soorten ze gedurende hun evolutie hebben kunnen ontdekken en er hun voordeel mee hebben kunnen doen om te overleven.
Ik heb het over verschillende soorten cicaden, zoals de Magicicada septendecium die in Noord-Amerika leeft. Deze cicadesoort heeft zijn broedcyclus vastgesteld rond 13 of 17 jaar, niet 12, 14, 15, 16, of 18 – precies 13 of 17. Hierdoor kunnen ze roofdieren vermijden die ook periodieke voortplantingscycli hebben; stel je een roofdier voor met een voortplantingscyclus van 4 jaar.
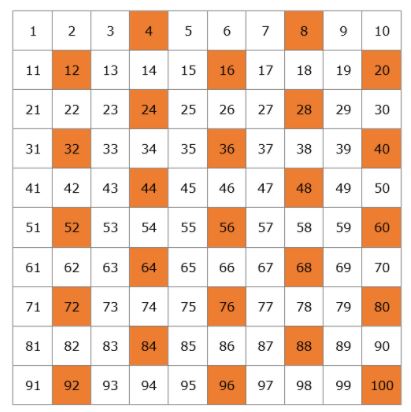
Als de levenscyclus van een cicade 12 of 14 jaar zou zijn, zou hij heel vaak samenvallen met een roofdier, veel vaker dan wanneer hij 13 of 17 jaar zou zijn. Precies 2 keer in de 100 jaar, terwijl ze anders in 11 cycli zouden samenvallen, wat de ontwikkeling van de soort in gevaar zou brengen.
De veiligheid van elektronische communicatie is ook gebaseerd op priemgetallen. Aan elk versleuteld bericht dat over het internet wordt verzonden (berichtennetwerken, aankopen of elektronisch bankieren) is een groot getal verbonden, en het is zeer moeilijk te weten of het priem is of niet. De ontvanger heeft één van zijn delers, en daarom kunnen zij het ontcijferen. Het hebben van priemgetallen is dus van cruciaal belang voor onze privacy bij elektronische communicatie.
Wat zijn samengestelde getallen?
Samengestelde getallen zijn getallen die deelbaar zijn door 1 en zichzelf en door andere getallen.
We gaan een voorbeeld bekijken van een priemgetal en een samengesteld getal.
11 kan worden geschreven als de vermenigvuldiging 1 x 11, maar het kan niet worden geschreven als een andere vermenigvuldiging van natuurlijke getallen. Het heeft alleen de delers 1 en 11, en daarom is het een priemgetal.
12 kan geschreven worden als de vermenigvuldiging 1 x 12 en als de vermenigvuldiging 3 x 4, en 2 x 6. Omdat 12 deelbaar is door meer getallen dan 1 en zichzelf, is 12 een samengesteld getal.
Is 1 een priemgetal?
Er zijn mensen die dat denken omdat zij zeggen dat 1 alleen deelbaar is door 1 en zichzelf, maar in de wiskunde is het getal 1 afgedaan als priemgetal omdat het maar één deler heeft. In feite wordt het criterium “een positief geheel getal is priem als het precies twee positieve delers heeft” gebruikt om het getal 1 van de lijst van priemgetallen uit te sluiten. Het is niet omdat we er kieskeurig over zijn, maar als het getal 1 als priem beschouwd zou worden, dan zouden veel wiskundige eigenschappen anders gezegd moeten worden.
Dus, 1 is een samengesteld getal?
Wel, het is ook niet samengesteld omdat het niet als het product van priemgetallen kan gesteld worden. Het getal 1 is niet priem of samengesteld. En voordat u het vraagt, nul is ook geen priemgetal of samengesteld getal, maar dat komt omdat alle overwegingen die we voor positieve getallen hebben uitgelegd, dus groter dan nul.
Delers van een getal
De deler van een getal is de waarde die het getal in exacte delen verdeelt, met andere woorden, een rest van 0 heeft.
Als voorbeeld gaan we de delers van 24 berekenen.
We beginnen te delen met de kleinste getallen, te beginnen met 1.
- 24 / 1 = 24. Zowel 1 als 24 zijn delers.
- 24 / 2 = 12. Dus 2 en 12 zijn delers.
- 24 / 3 = 8. Dus 3 en 8 zijn delers.
- 24 / 4 = 6. Dus 4 en 6 zijn delers.
- 24 / 5 = 4. Het is geen exacte deling en heeft een rest van 4, dus 5 is geen deler.
Het volgende getal is 6, maar omdat we al weten dat 6 een deler is van 24 zijn we klaar met het berekenen van de delers voor 24.
Video: Factorisatie en priemgetallen
Als je meer wilt weten over priemgetallen en samengestelde getallen, bekijk dan de volgende video. Je leert ook het concept van factorisatie met behulp van de Montessoritabel.
Deze video is een van onze interactieve leerprogramma’s en, hoewel hij niet interactief is, kun je hem toch zo vaak bekijken als je wilt en met vrienden delen. Als u toegang wilt krijgen tot onze interactieve zelfstudies, registreer u dan bij Smartick! De online methode om kinderen van 4 tot 14 jaar te helpen bij het leren en oefenen van wiskunde.
Wil je verder leren over priemgetallen en de beste wiskunde aangepast aan jouw niveau, registreer je dan bij Smartick en probeer het gratis!
Lees meer:
- Priemgetallen en samengestelde getallen
- Priemgetallen: Een truc om ze te identificeren
- Prime Numbers: Hoe ze te vinden met de zeef van Eratosthenes
- Leren ontbinden in factoren van priemgetallen
- Activiteiten met priemgetallen met Smartick



- Auteur
- Recent Posts
Een multidisciplinair en multicultureel team bestaande uit wiskundigen, leraren, professoren en andere onderwijsprofessionals!
Zij streven ernaar de best mogelijke wiskundige inhoud te creëren.
- Voorbeelden van 3e graad wiskunde woordproblemen met oplossingen – 03/25/2021
- Opeenvolgende binnenhoeken: Wat ze zijn en hoe ze te vinden met voorbeelden – 03/11/2021
- Voorbeelden van tweede graad woordproblemen met oplossingen – 02/04/2021