Equations of SHM
Rozważmy klocek przymocowany do sprężyny na stole pozbawionym tarcia (rysunek). Położenie równowagi (położenie, w którym sprężyna nie jest ani rozciągnięta, ani ściśnięta) jest oznaczone jako x = 0 . W położeniu równowagi siła netto wynosi zero.
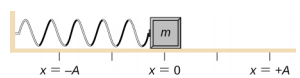
Pracujemy nad klockiem, aby wyciągnąć go do położenia x = + A, a następnie uwalniamy go ze stanu spoczynku. Maksymalne położenie x (A) nazywamy amplitudą ruchu. Blok zaczyna oscylować w SHM pomiędzy x = + A i x = -A, gdzie A jest amplitudą ruchu, a T jest okresem oscylacji. Okres jest czasem trwania jednej oscylacji. Rysunek rzedstawia ruch klocka, który kończy półtorej oscylacji po zwolnieniu.
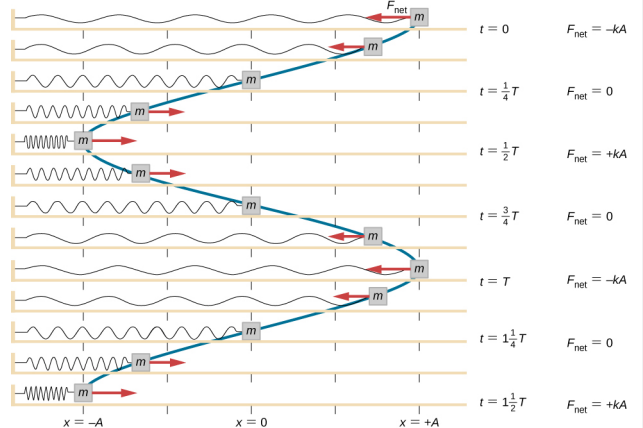
Równanie dla położenia w funkcji czasu \(x(t) = Acos( \omega t)\) jest dobre do modelowania danych, gdzie położenie klocka w początkowym czasie t = 0,00 s jest na amplitudzie A, a prędkość początkowa wynosi zero. Często podczas wykonywania danych doświadczalnych położenie masy w początkowym czasie t = 0,00 s nie jest równe amplitudzie, a prędkość początkowa nie jest równa zeru. Rozważmy 10 sekundowe dane zebrane przez studenta w laboratorium, pokazane na rysunku
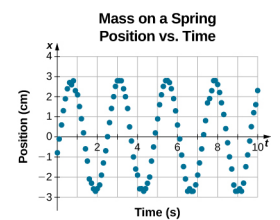
Dane na rysunku można nadal modelować za pomocą funkcji okresowej, takiej jak funkcja cosinusowa, ale funkcja ta jest przesunięta w prawo. To przesunięcie jest znane jako przesunięcie fazowe i jest zwykle reprezentowane przez grecką literę phi (∗phi). Równanie położenia w funkcji czasu dla bloku na sprężynie ma postać
Jest to uogólnione równanie dla SHM, gdzie t jest czasem mierzonym w sekundach, \(\omega\) jest częstotliwością kątową z jednostkami odwrotności sekund, A jest amplitudą mierzoną w metrach lub centymetrach, a \(\phi\) jest przesunięciem fazowym mierzonym w radianach (Rysunek \(\PageIndex{7}}). Należy zauważyć, że ponieważ funkcje sinus i cosinus różnią się tylko przesunięciem fazowym, ruch ten można modelować za pomocą funkcji cosinus lub sinus.
Prędkość masy na sprężynie, oscylującej w SHM, można znaleźć biorąc pochodną równania położenia:
Ponieważ funkcja sinusoidalna oscyluje pomiędzy -1 i +1, prędkość maksymalna jest amplitudą razy częstotliwość kątowa, vmax = A. Maksymalna prędkość występuje w położeniu równowagi (x = 0), gdy masa porusza się w kierunku x = + A. Maksymalna prędkość w kierunku ujemnym występuje w położeniu równowagi (x = 0), gdy masa porusza się w kierunku x = -A i jest równa -vmax.
Przyspieszenie masy na sprężynie można znaleźć, wykonując pochodną czasową prędkości