Równanie logistyczne (czasami nazywane modelem Verhulsta lub logistyczną krzywą wzrostu) jest modelem wzrostu populacji po raz pierwszy opublikowanym przez Pierre’a Verhulsta (1845, 1847). Model jest ciągły w czasie, ale modyfikacja ciągłego równania do dyskretnego kwadratowego równania rekurencyjnego, znanego jako mapa logistyczna, jest również szeroko stosowana.
Ciągła wersja modelu logistycznego opisana jest równaniem różniczkowym
 |
(1)
|
gdzie 
to parametr maltuzjański (tempo maksymalnego wzrostu populacji), a 
to tzw. pojemność nośna (czyli, maksymalna zrównoważona populacja). Dzieląc obie strony przez 
i definiując 
otrzymujemy równanie różniczkowe
 |
(2)
|
, które znane jest pod nazwą równania logistycznego i ma postać nazywamy równaniem logistycznym i ma rozwiązanie
 |
(3)
|
Funkcja 
jest czasami nazywana funkcją sigmoidalną.
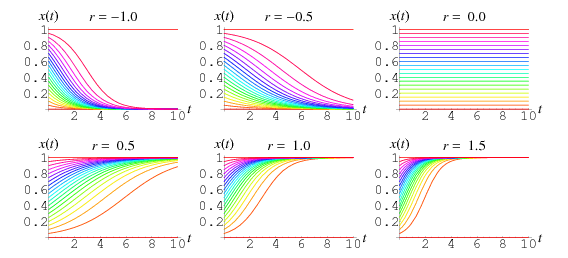
Pomimo że 
jest zwykle dodatnia, wykresy powyższego rozwiązania są pokazane dla różnych dodatnich i ujemnych wartości 
i warunków początkowych 
z zakresu od 0,00 do 1,00 w krokach co 0,05.
Dyskretna wersja równania logistycznego (3) jest znana jako mapa logistyczna.
Krzywa
 |
(4)
|
otrzymana z (3) jest czasami znana jako krzywa logistyczna. Podobnie, znormalizowana postać równania (3) jest powszechnie używana jako rozkład statystyczny znany jako rozkład logistyczny.
.