Regresja logistyczna

Regresja logistyczna (aka regresja logitowa lub model logitowy) została opracowana przez statystyka Davida Coxa w 1958 r. i jest modelem regresji, w którym zmienna odpowiedzi Y jest kategoryczna. Regresja logistyczna pozwala nam oszacować prawdopodobieństwo odpowiedzi kategorycznej w oparciu o jedną lub więcej zmiennych przewidujących (X). Pozwala to na stwierdzenie, że obecność predyktora zwiększa (lub zmniejsza) prawdopodobieństwo danego wyniku o określony procent. Ten poradnik omawia przypadek, gdy Y jest binarna – to znaczy, gdy może przyjąć tylko dwie wartości, „0” i „1”, które reprezentują wyniki takie jak pass/fail, win/lose, alive/dead lub healthy/sick. Przypadki, w których zmienna zależna ma więcej niż dwie kategorie wyników, mogą być analizowane za pomocą wielomianowej regresji logistycznej lub, jeżeli wiele kategorii jest uporządkowanych, za pomocą porządkowej regresji logistycznej. Jednakże, analiza dyskryminacyjna stała się popularną metodą klasyfikacji wieloklasowej, więc nasz następny tutorial skupi się na tej technice dla tych przypadków.

tl;dr

Ten tutorial służy jako wprowadzenie do regresji logistycznej i obejmuje1:

1. Wymagania dotyczące replikacji: Co będzie potrzebne do odtworzenia analizy w tym samouczku
2. Dlaczego regresja logistyczna: Dlaczego używać regresji logistycznej?
3. Przygotowanie naszych danych: Przygotuj nasze dane do modelowania
4. Prosta regresja logistyczna: Przewidywanie prawdopodobieństwa odpowiedzi Y za pomocą pojedynczej zmiennej predykcyjnej X
5. Wielokrotna regresja logistyczna: Przewidywanie prawdopodobieństwa odpowiedzi Y z wieloma zmiennymi predykcyjnymi
6. Ocena modelu & diagnostyka: Jak dobrze model pasuje do danych? Które predyktory są najważniejsze? Czy przewidywania są dokładne?

Wymagania replikacyjne

Tutorial ten wykorzystuje przede wszystkim dane Default dostarczone przez pakiet ISLR. Jest to symulowany zbiór danych zawierający informacje o dziesięciu tysiącach klientów, takie jak: czy klient nie wywiązuje się ze swoich zobowiązań, czy jest studentem, jakie jest jego średnie saldo oraz jaki jest jego dochód. Wykorzystamy również kilka pakietów, które zapewniają funkcje manipulacji danymi, wizualizacji, modelowania rurociągów oraz porządkowania danych wyjściowych modelu.

# Packageslibrary(tidyverse) # data manipulation and visualizationlibrary(modelr) # provides easy pipeline modeling functionslibrary(broom) # helps to tidy up model outputs# Load data (default <- as_tibble(ISLR::Default))## # A tibble: 10,000 × 4## default student balance income## <fctr> <fctr> <dbl> <dbl>## 1 No No 729.5265 44361.625## 2 No Yes 817.1804 12106.135## 3 No No 1073.5492 31767.139## 4 No No 529.2506 35704.494## 5 No No 785.6559 38463.496## 6 No Yes 919.5885 7491.559## 7 No No 825.5133 24905.227## 8 No Yes 808.6675 17600.451## 9 No No 1161.0579 37468.529## 10 No No 0.0000 29275.268## # ... with 9,990 more rows

Why Logistic Regression

Regresja liniowa nie jest odpowiednia w przypadku odpowiedzi jakościowej. Dlaczego nie? Załóżmy, że próbujemy przewidzieć stan medyczny pacjentki w izbie przyjęć na podstawie jej objawów. W tym uproszczonym przykładzie istnieją trzy możliwe diagnozy: udar, przedawkowanie leków i napad padaczkowy. Moglibyśmy rozważyć zakodowanie tych wartości jako ilościowej zmiennej odpowiedzi, Y , w następujący sposób:

Używając tego kodowania, można by użyć najmniejszych kwadratów do dopasowania modelu regresji liniowej, aby przewidzieć Y na podstawie zestawu predyktorów . Niestety, takie kodowanie implikuje uporządkowanie wyników, umieszczając przedawkowanie leków pomiędzy udarem a napadem padaczkowym i nalegając, aby różnica pomiędzy udarem a przedawkowaniem leków była taka sama jak różnica pomiędzy przedawkowaniem leków a napadem padaczkowym. W praktyce nie ma żadnego szczególnego powodu, aby tak musiało być. Na przykład, można wybrać równie rozsądne kodowanie

, które sugerowałoby zupełnie inny związek między tymi trzema stanami. Każde z tych kodowań dałoby zasadniczo różne modele liniowe, które ostatecznie doprowadziłyby do różnych zestawów przewidywań dotyczących obserwacji testowych.

W odniesieniu do naszych danych, jeśli próbujemy zaklasyfikować klienta do grupy wysokiego lub niskiego ryzyka niewywiązania się ze zobowiązań na podstawie jego salda, moglibyśmy zastosować regresję liniową; jednakże lewy poniższy rysunek ilustruje, w jaki sposób regresja liniowa przewidziałaby prawdopodobieństwo niewywiązania się ze zobowiązań. Niestety, dla sald bliskich zeru przewidujemy ujemne prawdopodobieństwo niewywiązania się ze zobowiązań; gdybyśmy mieli przewidywać dla bardzo dużych sald, otrzymalibyśmy wartości większe od 1. Te przewidywania nie są sensowne, ponieważ oczywiście prawdziwe prawdopodobieństwo niewywiązania się ze zobowiązań, niezależnie od salda karty kredytowej, musi mieścić się w przedziale od 0 do 1.

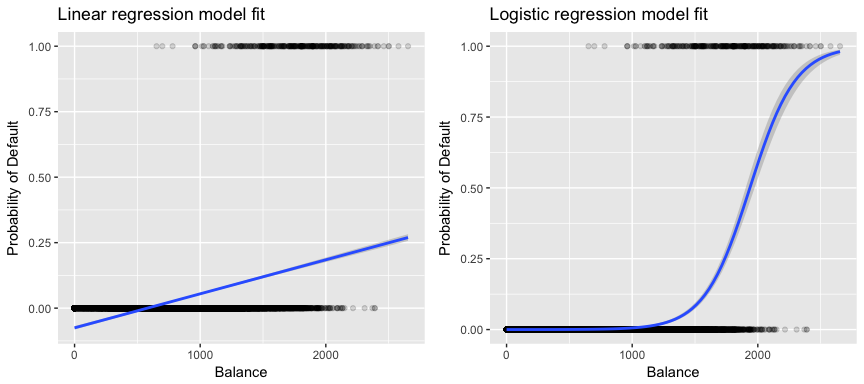
Aby uniknąć tego problemu, musimy modelować p(X) za pomocą funkcji, która daje wyniki w przedziale od 0 do 1 dla wszystkich wartości X. Wiele funkcji spełnia ten opis. W regresji logistycznej używamy funkcji logistycznej, która jest zdefiniowana w równaniu 1 i zilustrowana na prawym rysunku powyżej.

Przygotowanie danych

Podobnie jak w samouczku regresji, podzielimy nasze dane na zbiór treningowy (60%) i testowy (40%), abyśmy mogli ocenić, jak dobrze nasz model działa na zbiorze danych poza próbą.

set.seed(123)sample <- sample(c(TRUE, FALSE), nrow(default), replace = T, prob = c(0.6,0.4))train <- defaulttest <- default

Prosta regresja logistyczna

Zastosujemy model regresji logistycznej, aby przewidzieć prawdopodobieństwo niewywiązania się klienta ze zobowiązań na podstawie średniego salda posiadanego przez klienta. Funkcja glm dopasowuje uogólnione modele liniowe, klasę modeli, która obejmuje regresję logistyczną. Składnia funkcji glm jest podobna do składni funkcji lm, z wyjątkiem tego, że musimy przekazać argument family = binomial, aby powiedzieć R, aby uruchomił regresję logistyczną, a nie jakiś inny typ uogólnionego modelu liniowego.

model1 <- glm(default ~ balance, family = "binomial", data = train)

W tle funkcja glm, używa maksymalnego prawdopodobieństwa do dopasowania modelu. Podstawowa intuicja stojąca za wykorzystaniem największego prawdopodobieństwa do dopasowania modelu regresji logistycznej jest następująca: szukamy oszacowań dla i, tak aby przewidywane prawdopodobieństwo niewykonania zobowiązania dla każdej osoby, przy użyciu równania 1, jak najdokładniej odpowiadało zaobserwowanemu statusowi niewykonania zobowiązania przez daną osobę. Innymi słowy, staramy się znaleźć i w taki sposób, aby wstawienie tych oszacowań do modelu dla p(X), podanego w równaniu 1, dało liczbę bliską jeden dla wszystkich osób, które nie wywiązały się ze zobowiązań i liczbę bliską zero dla wszystkich osób, które się nie wywiązały. Ta intuicja może być sformalizowana przy użyciu równania matematycznego zwanego funkcją prawdopodobieństwa:

Oszacowania i są wybierane tak, aby zmaksymalizować tę funkcję prawdopodobieństwa. Maksymalne prawdopodobieństwo jest bardzo ogólnym podejściem, które jest używane do dopasowania wielu nieliniowych modeli, które będziemy badać w przyszłych tutorialach. Wynikiem jest krzywa prawdopodobieństwa w kształcie litery S, zilustrowana poniżej (zauważ, że aby wykreślić linię dopasowania regresji logistycznej, musimy przekształcić naszą zmienną odpowiedzi na zmienną kodowaną binarnie).

default %>% mutate(prob = ifelse(default == "Yes", 1, 0)) %>% ggplot(aes(balance, prob)) + geom_point(alpha = .15) + geom_smooth(method = "glm", method.args = list(family = "binomial")) + ggtitle("Logistic regression model fit") + xlab("Balance") + ylab("Probability of Default")

Podobnie jak w przypadku regresji liniowej, możemy ocenić model za pomocą summary lub glance. Zauważ, że format wyjściowy współczynnika jest podobny do tego, który widzieliśmy w regresji liniowej; jednak szczegóły dotyczące dobroci dopasowania na dole summary różnią się. Zajmiemy się tym bardziej później, ale zauważ, że widzisz słowo deviance. Odchylenie jest analogiczne do sumy kwadratów obliczeń w regresji liniowej i jest miarą braku dopasowania do danych w modelu regresji logistycznej. Odchylenie zerowe reprezentuje różnicę pomiędzy modelem z tylko przechwytem (co oznacza „brak predyktorów”) a modelem nasyconym (model z teoretycznie doskonałym dopasowaniem). Celem jest, aby odchylenie modelu (oznaczone jako odchylenie rezydualne) było niższe; mniejsze wartości wskazują na lepsze dopasowanie. W tym względzie, model zerowy zapewnia punkt odniesienia, na którym można porównać modele predyktorów.

summary(model1)## ## Call:## glm(formula = default ~ balance, family = "binomial", data = train)## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -2.2905 -0.1395 -0.0528 -0.0189 3.3346 ## ## Coefficients:## Estimate Std. Error z value Pr(>|z|) ## (Intercept) -1.101e+01 4.887e-01 -22.52 <2e-16 ***## balance 5.669e-03 2.949e-04 19.22 <2e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## (Dispersion parameter for binomial family taken to be 1)## ## Null deviance: 1723.03 on 6046 degrees of freedom## Residual deviance: 908.69 on 6045 degrees of freedom## AIC: 912.69## ## Number of Fisher Scoring iterations: 8

Ocena współczynników

Poniższa tabela przedstawia oszacowania współczynników i związane z nimi informacje, które wynikają z dopasowania modelu regresji logistycznej w celu przewidzenia prawdopodobieństwa niewykonania zobowiązania = Tak przy użyciu salda. Należy pamiętać, że oszacowania współczynników regresji logistycznej charakteryzują związek między zmienną przewidywaną i zmienną odpowiedzi w skali log-odds (zobacz rozdział 3 ISLR1, aby uzyskać więcej szczegółów). Tak więc widzimy, że ; wskazuje to, że wzrost salda wiąże się ze wzrostem prawdopodobieństwa niewywiązania się ze zobowiązań. Dokładniej, wzrost salda o jedną jednostkę wiąże się ze wzrostem log prawdopodobieństwa niewykonania zobowiązania o 0,0057 jednostki.

tidy(model1)## term estimate std.error statistic p.value## 1 (Intercept) -11.006277528 0.488739437 -22.51972 2.660162e-112## 2 balance 0.005668817 0.000294946 19.21985 2.525157e-82

Współczynnik salda możemy dalej interpretować jako – dla każdego dolara wzrostu miesięcznego salda, prawdopodobieństwo niewykonania zobowiązania przez klienta wzrasta o współczynnik 1.0057.

exp(coef(model1))## (Intercept) balance ## 1.659718e-05 1.005685e+00

Wiele aspektów danych wyjściowych współczynnika jest podobnych do tych omówionych w danych wyjściowych regresji liniowej. Na przykład, możemy zmierzyć przedziały ufności i dokładność oszacowań współczynników poprzez obliczenie ich błędów standardowych. Na przykład, wartość p < 2e-16 sugeruje statystycznie istotny związek między saldem bilansowym a prawdopodobieństwem niewywiązania się z zobowiązań. Możemy również użyć błędów standardowych, aby uzyskać przedziały ufności, tak jak to zrobiliśmy w samouczku regresji liniowej:

confint(model1)## 2.5 % 97.5 %## (Intercept) -12.007610373 -10.089360652## balance 0.005111835 0.006269411

Stwarzanie przewidywań

Po oszacowaniu współczynników prostą sprawą jest obliczenie prawdopodobieństwa niewykonania zobowiązania dla dowolnego danego salda karty kredytowej. Matematycznie, używając oszacowań współczynników z naszego modelu przewidujemy, że prawdopodobieństwo niewypłacalności dla osoby z saldem 1000 dolarów jest mniejsze niż 0,5%

Możemy przewidzieć prawdopodobieństwo niewypłacalności w R używając funkcji predict (upewnij się, że dołączyłeś type = "response"). Tutaj porównujemy prawdopodobieństwo niewywiązania się z płatności na podstawie sald 1000 i 2000 dolarów. Jak widać, gdy saldo przesuwa się z $1000 do $2000, prawdopodobieństwo niewykonania zobowiązania wzrasta znacząco, z 0,5% do 58%!

predict(model1, data.frame(balance = c(1000, 2000)), type = "response")## 1 2 ## 0.004785057 0.582089269

Można również użyć predyktorów jakościowych w modelu regresji logistycznej. Jako przykład, możemy dopasować model, który wykorzystuje zmienną student.

model2 <- glm(default ~ student, family = "binomial", data = train)tidy(model2)## term estimate std.error statistic p.value## 1 (Intercept) -3.5534091 0.09336545 -38.05914 0.000000000## 2 studentYes 0.4413379 0.14927208 2.95660 0.003110511

Współczynnik związany z student = Yes jest dodatni, a związana z nim wartość p jest statystycznie istotna. Wskazuje to, że studenci mają wyższe prawdopodobieństwo niewywiązania się z zobowiązań niż osoby niebędące studentami. W rzeczywistości model ten sugeruje, że student ma prawie dwukrotnie wyższe prawdopodobieństwo niewywiązania się z zobowiązań niż osoby niebędące studentami. Jednakże, w następnej sekcji zobaczymy dlaczego.

predict(model2, data.frame(student = factor(c("Yes", "No"))), type = "response")## 1 2 ## 0.04261206 0.02783019

Wielokrotna regresja logistyczna

Możemy również rozszerzyć nasz model, jak widać w równ. 1 tak, że możemy przewidzieć odpowiedź binarną używając wielu predyktorów, gdzie są p predyktory:

Przejdźmy dalej i dopasujmy model, który przewiduje prawdopodobieństwo niewykonania zobowiązania w oparciu o zmienne salda, dochodu (w tysiącach dolarów) i statusu studenta. Mamy tu zaskakujący wynik. Wartości p związane z saldem i statusem studenta=Tak są bardzo małe, co wskazuje, że każda z tych zmiennych jest związana z prawdopodobieństwem niewywiązania się ze zobowiązań. Jednak współczynnik dla zmiennej student jest ujemny, co wskazuje, że studenci są mniej skłonni do niewywiązywania się ze zobowiązań niż osoby niebędące studentami. W przeciwieństwie do tego, współczynnik dla zmiennej studenta w modelu 2, gdzie przewidywaliśmy prawdopodobieństwo niewywiązania się ze zobowiązań tylko na podstawie statusu studenta, wskazywał, że studenci mają większe prawdopodobieństwo niewywiązania się ze zobowiązań. Co z tego wynika?

model3 <- glm(default ~ balance + income + student, family = "binomial", data = train)tidy(model3)## term estimate std.error statistic p.value## 1 (Intercept) -1.090704e+01 6.480739e-01 -16.8299277 1.472817e-63## 2 balance 5.907134e-03 3.102425e-04 19.0403764 7.895817e-81## 3 income -5.012701e-06 1.078617e-05 -0.4647343 6.421217e-01## 4 studentYes -8.094789e-01 3.133150e-01 -2.5835947 9.777661e-03

Prawy panel poniższego rysunku dostarcza wyjaśnienia tej rozbieżności. Zmienne student i saldo są ze sobą skorelowane. Studenci mają tendencję do posiadania wyższego poziomu zadłużenia, co z kolei wiąże się z wyższym prawdopodobieństwem niewywiązania się ze zobowiązań. Innymi słowy, studenci częściej mają wysokie salda na kartach kredytowych, które, jak wiadomo z lewego panelu poniższego rysunku, wiążą się z wysokim wskaźnikiem niewypłacalności. Zatem nawet jeśli prawdopodobieństwo niewywiązania się ze zobowiązań przez pojedynczego studenta z danym saldem na karcie kredytowej jest niższe niż prawdopodobieństwo niewywiązania się ze zobowiązań przez osobę niebędącą studentem z takim samym saldem na karcie kredytowej, fakt, że studenci jako całość mają wyższe salda na kartach kredytowych, oznacza, że ogólnie rzecz biorąc, studenci częściej niż osoby niebędące studentami nie wywiązują się ze zobowiązań. Jest to ważne rozróżnienie dla firmy wydającej karty kredytowe, która próbuje określić, komu powinna zaoferować kredyt. Student jest bardziej ryzykowny niż osoba niebędąca studentem, jeśli nie są dostępne żadne informacje o jego saldzie na karcie kredytowej. Jednak ten student jest mniej ryzykowny niż osoba niebędąca studentem z takim samym saldem na karcie kredytowej!

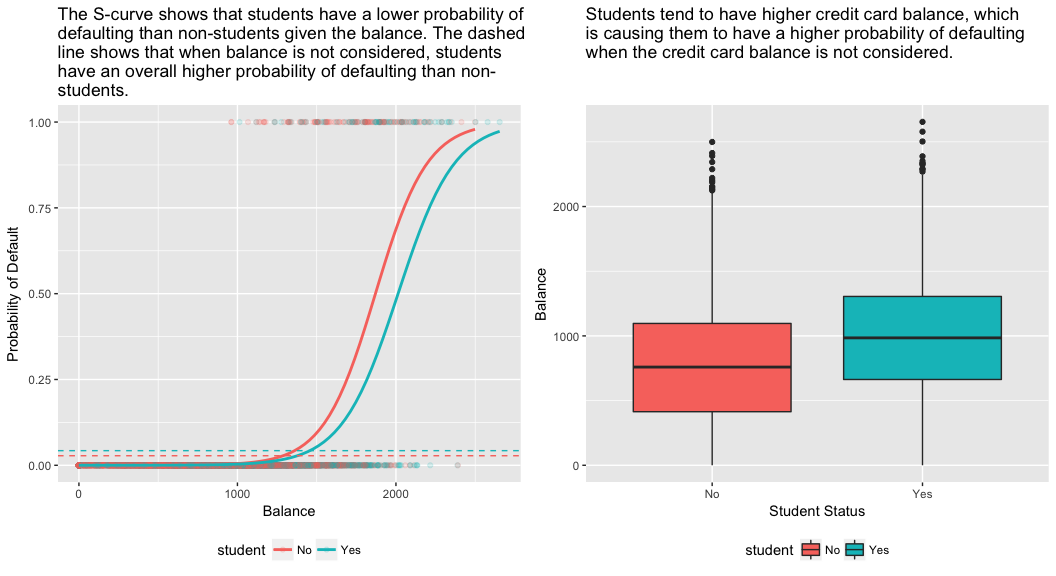
Ten prosty przykład ilustruje niebezpieczeństwa i subtelności związane z wykonywaniem regresji obejmujących tylko jeden predyktor, gdy inne predyktory mogą być również istotne. Wyniki uzyskane przy użyciu jednego predyktora mogą być całkiem inne od tych uzyskanych przy użyciu wielu predyktorów, zwłaszcza gdy istnieje korelacja między predyktorami. Zjawisko to znane jest jako konfundacja.

W przypadku wielu zmiennych przewidujących czasami chcemy zrozumieć, która zmienna jest najbardziej wpływowa w przewidywaniu zmiennej odpowiedzi (Y). Możemy to zrobić za pomocą varImp z pakietu caret. Widzimy tutaj, że saldo jest najważniejsze z dużym marginesem, podczas gdy status studenta jest mniej ważny, a następnie dochód (który i tak okazał się nieistotny (p = .64)).

caret::varImp(model3)## Overall## balance 19.0403764## income 0.4647343## studentYes 2.5835947

Jak poprzednio, możemy łatwo dokonać przewidywań za pomocą tego modelu. Na przykład, student z saldem na karcie kredytowej wynoszącym 1500 USD i dochodem 40 000 USD ma szacunkowe prawdopodobieństwo niewykonania zobowiązania

Student niebędący studentem z takim samym saldem i dochodem ma szacunkowe prawdopodobieństwo niewykonania zobowiązania

new.df <- tibble(balance = 1500, income = 40, student = c("Yes", "No"))predict(model3, new.df, type = "response")## 1 2 ## 0.05437124 0.11440288

W ten sposób widzimy, że dla danego salda i dochodu (chociaż dochód jest nieistotny) student ma około połowę mniejsze prawdopodobieństwo niewykonania zobowiązania niż osoba niebędąca studentem.

Ocena modelu &Diagnostyka

Do tej pory zbudowano trzy modele regresji logistycznej i zbadano ich współczynniki. Pozostaje jednak kilka krytycznych pytań. Czy te modele są dobre? Jak dobrze model pasuje do danych? I jak dokładne są przewidywania na zbiorze danych poza próbą?

Goodness-of-Fit

W samouczku regresji liniowej widzieliśmy, jak statystyka F i skorygowana , oraz diagnostyka reszt informują nas o tym, jak dobrze model pasuje do danych. Tutaj, przyjrzymy się kilku sposobom oceny dobroci dopasowania dla naszych modeli logitowych.

Test współczynnika prawdopodobieństwa

Po pierwsze, możemy użyć testu współczynnika prawdopodobieństwa, aby ocenić, czy nasze modele poprawiają dopasowanie. Dodanie zmiennych predykcyjnych do modelu prawie zawsze poprawi dopasowanie modelu (tj. zwiększy prawdopodobieństwo logiczne i zmniejszy odchylenie modelu w porównaniu z odchyleniem zerowym), ale konieczne jest sprawdzenie, czy zaobserwowana różnica w dopasowaniu modelu jest statystycznie istotna. Do wykonania tego testu możemy użyć anova. Wyniki wskazują, że w porównaniu do model1, model3 zmniejsza odchylenie resztowe o ponad 13 (pamiętajmy, że celem regresji logistycznej jest znalezienie modelu, który minimalizuje odchylenie resztowe). Co ważniejsze, poprawa ta jest statystycznie istotna przy p = 0,001. Sugeruje to, że model3 zapewnia lepsze dopasowanie modelu.

anova(model1, model3, test = "Chisq")## Analysis of Deviance Table## ## Model 1: default ~ balance## Model 2: default ~ balance + income + student## Resid. Df Resid. Dev Df Deviance Pr(>Chi) ## 1 6045 908.69 ## 2 6043 895.02 2 13.668 0.001076 **## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Pseudo

W przeciwieństwie do regresji liniowej ze zwykłą estymacją najmniejszych kwadratów, nie ma statystyki, która wyjaśnia, jaka część wariancji w zmiennej zależnej jest wyjaśniona przez predyktory. Jakkolwiek, tam być liczba pseudo metryka który móc wartość. Najbardziej godna uwagi jest McFadden’s , która jest zdefiniowana jako

gdzie jest wartością log prawdopodobieństwa dla dopasowanego modelu i jest log prawdopodobieństwem dla modelu zerowego z tylko przechwytem jako predyktorem. Miara ta waha się od 0 do nieco poniżej 1, przy czym wartości bliższe zeru wskazują, że model nie ma mocy predykcyjnej. Jednakże, w przeciwieństwie do regresji liniowej, modele rzadko osiągają wysoki wynik McFaddena . W rzeczywistości, według słów samego McFaddena, modele z pseudo McFaddenem reprezentują bardzo dobre dopasowanie. Możemy ocenić wartości pseudo McFaddena dla naszych modeli za pomocą:

list(model1 = pscl::pR2(model1), model2 = pscl::pR2(model2), model3 = pscl::pR2(model3))## $model1## McFadden ## 0.4726215 ## ## $model2## McFadden ## 0.004898314 ## ## $model3## McFadden ## 0.4805543

Widzimy, że model 2 ma bardzo niską wartość potwierdzającą jego słabe dopasowanie. Jednak modele 1 i 3 mają znacznie wyższe wartości, co sugeruje, że wyjaśniają one znaczną część wariancji w danych domyślnych. Ponadto widzimy, że model 3 tylko nieznacznie poprawia wynik.

Ocena reszt

Należy pamiętać, że regresja logistyczna nie zakłada, że reszty mają rozkład normalny ani że wariancja jest stała. Jednakże, odchylenie reszt jest przydatne do określenia, czy poszczególne punkty nie są dobrze dopasowane przez model. Tutaj możemy dopasować standaryzowane reszty dewiancji, aby zobaczyć, ile z nich przekracza 3 odchylenia standardowe. Najpierw wyodrębniamy kilka przydatnych fragmentów wyników modelu za pomocą augment, a następnie przechodzimy do wykreślania.

model1_data <- augment(model1) %>% mutate(index = 1:n())ggplot(model1_data, aes(index, .std.resid, color = default)) + geom_point(alpha = .5) + geom_ref_line(h = 3)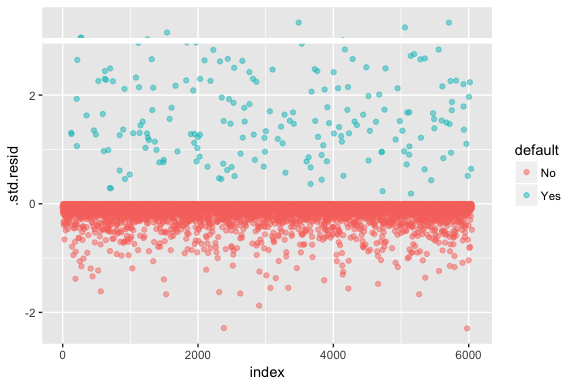

Te znormalizowane reszty, które przekraczają 3, reprezentują możliwe wartości odstające i mogą zasługiwać na większą uwagę. Możemy przefiltrować te resztki, aby przyjrzeć się im bliżej. Widzimy, że wszystkie te obserwacje reprezentują klientów, którzy nie wywiązują się z płatności z budżetami, które są znacznie niższe niż normalne osoby niewywiązujące się z płatności.

model1_data %>% filter(abs(.std.resid) > 3)## default balance .fitted .se.fit .resid .hat .sigma .cooksd .std.resid index## 1 Yes 1118.7010 -4.664566 0.1752745 3.057432 0.0002841609 0.3857438 0.01508609 3.057867 271## 2 Yes 1119.0972 -4.662320 0.1751742 3.056704 0.0002844621 0.3857448 0.01506820 3.057139 272## 3 Yes 1135.0473 -4.571902 0.1711544 3.027272 0.0002967274 0.3857832 0.01435943 3.027721 1253## 4 Yes 1066.8841 -4.958307 0.1885550 3.151288 0.0002463229 0.3856189 0.01754100 3.151676 1542## 5 Yes 961.4889 -5.555773 0.2163846 3.334556 0.0001796165 0.3853639 0.02324417 3.334855 3488## 6 Yes 1143.6805 -4.522962 0.1689933 3.011233 0.0003034789 0.3858039 0.01398491 3.011690 4142## 7 Yes 1013.2169 -5.262537 0.2026075 3.245830 0.0002105772 0.3854892 0.02032614 3.246172 5058## 8 Yes 961.7327 -5.554391 0.2163192 3.334143 0.0001797543 0.3853645 0.02322988 3.334443 5709

Podobnie jak w przypadku regresji liniowej możemy również zidentyfikować wpływowe obserwacje za pomocą wartości odległości Cooka. Tutaj identyfikujemy 5 największych wartości.

plot(model1, which = 4, id.n = 5)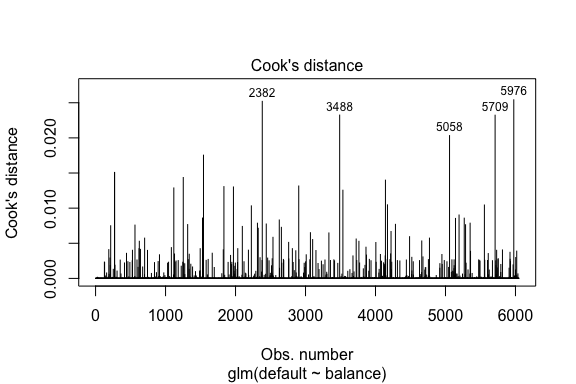

I te wartości również możemy dalej badać. Widzimy, że pięć najbardziej wpływowych punktów obejmuje:

• klientów, którzy nie wywiązali się ze zobowiązań przy bardzo niskich saldach oraz
• dwóch klientów, którzy nie wywiązali się ze zobowiązań, ale mieli salda powyżej 2000 USD

Oznacza to, że gdybyśmy usunęli te obserwacje (niezalecane), kształt, lokalizacja i przedział ufności naszej krzywej S regresji logistycznej prawdopodobnie uległyby zmianie.

model1_data %>% top_n(5, .cooksd)## default balance .fitted .se.fit .resid .hat .sigma .cooksd .std.resid index## 1 No 2388.1740 2.531843 0.2413764 -2.284011 0.0039757771 0.3866249 0.02520100 -2.288565 2382## 2 Yes 961.4889 -5.555773 0.2163846 3.334556 0.0001796165 0.3853639 0.02324417 3.334855 3488## 3 Yes 1013.2169 -5.262537 0.2026075 3.245830 0.0002105772 0.3854892 0.02032614 3.246172 5058## 4 Yes 961.7327 -5.554391 0.2163192 3.334143 0.0001797543 0.3853645 0.02322988 3.334443 5709## 5 No 2391.0077 2.547907 0.2421522 -2.290521 0.0039468742 0.3866185 0.02542145 -2.295054 5976

Weryfikacja przewidywanych wartości

Stopa klasyfikacji

Przy opracowywaniu modeli predykcji, najbardziej krytyczną metryką jest to, jak dobrze model radzi sobie z przewidywaniem zmiennej docelowej na obserwacjach poza próbą. Po pierwsze, musimy użyć oszacowanych modeli do przewidywania wartości na naszym zestawie danych treningowych (train). Podczas korzystania z predict należy pamiętać o dołączeniu type = response, aby predykcja zwracała prawdopodobieństwo domyślne.

test.predicted.m1 <- predict(model1, newdata = test, type = "response")test.predicted.m2 <- predict(model2, newdata = test, type = "response")test.predicted.m3 <- predict(model3, newdata = test, type = "response")

Teraz możemy porównać przewidywaną zmienną docelową z wartościami obserwowanymi dla każdego modelu i zobaczyć, który z nich wypada najlepiej. Możemy zacząć od użycia macierzy konfuzji, która jest tabelą opisującą wydajność klasyfikacji dla każdego modelu na danych testowych. Każdy kwadrant tabeli ma ważne znaczenie. W tym przypadku „Nie” i „Tak” w wierszach reprezentują, czy klienci zalegają z płatnościami, czy nie. FAŁSZ” i „PRAWDA” w kolumnach oznaczają, czy przewidzieliśmy, że klienci będą zalegać z płatnościami czy nie.

• wyniki prawdziwie pozytywne (prawy dolny kwadrant): są to przypadki, w których przewidzieliśmy, że klient będzie zalegał z płatnościami i tak się stało.
• wyniki prawdziwie negatywne (lewy górny kwadrant): Przewidzieliśmy brak niewykonania zobowiązania, a klient nie wykonał zobowiązania.
• wyniki fałszywie dodatnie (Prawy górny kwadrant): Przewidzieliśmy, że tak, ale w rzeczywistości nie doszło do niewykonania zobowiązania. (Znany również jako „błąd typu I.”)
• fałszywe negatywy (dolny lewy kwadrat): Przewidzieliśmy, że nie, ale oni rzeczywiście nie wywiązali się z umowy. (Znane również jako „błąd typu II.”)

Wyniki pokazują, że model1 i model3 są bardzo podobne. 96% przewidywanych obserwacji to prawdziwe negatywy, a około 1% to prawdziwe pozytywy. Oba modele mają błąd typu II wynoszący mniej niż 3%, w którym model przewiduje, że klient nie będzie zalegał z płatnościami, ale w rzeczywistości tak się stało. I oba modele mają błąd typu I mniejszy niż 1%, w którym model przewiduje, że klient nie wywiąże się z umowy, ale nigdy tego nie zrobił. model2 wyniki są znacząco różne; ten model dokładnie przewiduje klientów, którzy nie zalegają z płatnościami (wynik 97% danych to klienci, którzy nie zalegają z płatnościami), ale nigdy nie przewiduje tych klientów, którzy zalegają z płatnościami!

list( model1 = table(test$default, test.predicted.m1 > 0.5) %>% prop.table() %>% round(3), model2 = table(test$default, test.predicted.m2 > 0.5) %>% prop.table() %>% round(3), model3 = table(test$default, test.predicted.m3 > 0.5) %>% prop.table() %>% round(3))## $model1## ## FALSE TRUE## No 0.962 0.003## Yes 0.025 0.010## ## $model2## ## FALSE## No 0.965## Yes 0.035## ## $model3## ## FALSE TRUE## No 0.963 0.003## Yes 0.026 0.009

Chcemy również zrozumieć współczynniki błędnej klasyfikacji (aka błędów) (lub możemy to zamienić na współczynniki dokładności). Nie widzimy dużej poprawy pomiędzy modelami 1 i 3 i chociaż model 2 ma niską stopę błędu, nie zapominajmy, że nigdy dokładnie nie przewiduje klientów, którzy faktycznie nie wywiązują się ze zobowiązań.

test %>% mutate(m1.pred = ifelse(test.predicted.m1 > 0.5, "Yes", "No"), m2.pred = ifelse(test.predicted.m2 > 0.5, "Yes", "No"), m3.pred = ifelse(test.predicted.m3 > 0.5, "Yes", "No")) %>% summarise(m1.error = mean(default != m1.pred), m2.error = mean(default != m2.pred), m3.error = mean(default != m3.pred))## # A tibble: 1 × 3## m1.error m2.error m3.error## <dbl> <dbl> <dbl>## 1 0.02782697 0.03491019 0.02807994

Możemy uzyskać pewne dodatkowe spostrzeżenia, patrząc na surowe wartości (nie procenty) w naszej macierzy konfuzji. Spójrzmy na model 1, aby to zilustrować. Widzimy, że istnieje całkowita liczba klientów, którzy nie wywiązali się z umowy. Spośród wszystkich przypadków niewywiązania się z płatności, nie były one przewidywane. Alternatywnie, możemy powiedzieć, że tylko niektóre przypadki niewykonania zobowiązania zostały przewidziane – jest to znane jako precyzja (znana również jako czułość) naszego modelu. Tak więc, podczas gdy ogólny poziom błędów jest niski, poziom precyzji jest również niski, co nie jest dobre!

table(test$default, test.predicted.m1 > 0.5)## ## FALSE TRUE## No 3803 12## Yes 98 40

W przypadku modeli klasyfikacyjnych będziesz również używał terminów czułość i specyficzność przy charakteryzowaniu wydajności modelu. Jak wspomniano powyżej, czułość jest synonimem precyzji. Jednakże, specyficzność jest procentem nie-wykonawców, którzy są poprawnie zidentyfikowani, tutaj (dokładność tutaj jest w dużej mierze napędzana przez fakt, że 97% obserwacji w naszych danych to nie-wykonawcy). Znaczenie pomiędzy wrażliwością a specyficznością zależy od kontekstu. W tym przypadku, firma obsługująca karty kredytowe będzie prawdopodobnie bardziej zainteresowana wrażliwością, ponieważ chce zmniejszyć swoje ryzyko. Dlatego może być bardziej zainteresowana dostrojeniem modelu tak, aby poprawić jego czułość/precyzję.

Odbiór charakterystyki operacyjnej (ROC) jest wizualną miarą wydajności klasyfikatora. Używając proporcji pozytywnych punktów danych, które są poprawnie uważane za pozytywne i proporcji negatywnych punktów danych, które są błędnie uważane za pozytywne, generujemy grafikę, która pokazuje kompromis między tempem, w którym można poprawnie przewidzieć coś z tempem nieprawidłowego przewidywania czegoś. Ostatecznie, interesuje nas obszar pod krzywą ROC, lub AUC. Ta metryka waha się od 0,50 do 1,00, a wartości powyżej 0,80 wskazują, że model wykonuje dobrą pracę w rozróżnianiu pomiędzy dwoma kategoriami, które składają się na naszą zmienną docelową. Możemy porównać ROC i AUC dla modelu 1 i 2, które pokazują silną różnicę w wydajności. Zdecydowanie chcemy, aby nasze wykresy ROC wyglądały bardziej jak wykres modelu 1 (po lewej) niż modelu 2 (po prawej)!

library(ROCR)par(mfrow=c(1, 2))prediction(test.predicted.m1, test$default) %>% performance(measure = "tpr", x.measure = "fpr") %>% plot()prediction(test.predicted.m2, test$default) %>% performance(measure = "tpr", x.measure = "fpr") %>% plot()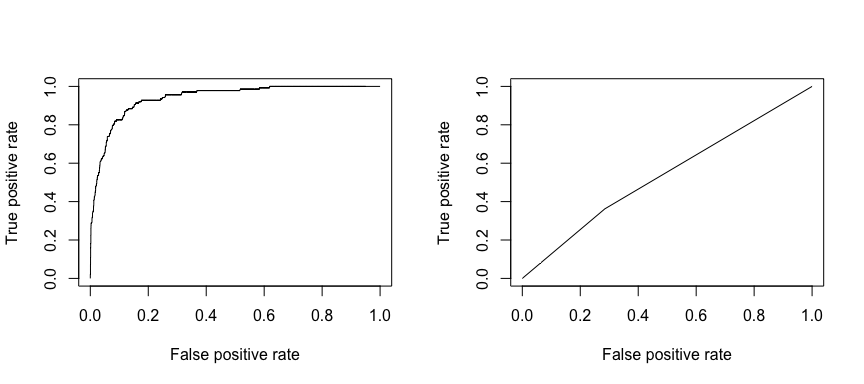

Aby obliczyć AUC liczbowo, możemy użyć następującego wzoru. Pamiętajmy, że AUC będzie się mieścił w przedziale .50 – 1.00. Zatem model 2 jest bardzo słabym modelem klasyfikującym, podczas gdy model 1 jest bardzo dobrym modelem klasyfikującym.

# model 1 AUCprediction(test.predicted.m1, test$default) %>% performance(measure = "auc") %>% [email protected]## ]## 0.939932# model 2 AUCprediction(test.predicted.m2, test$default) %>% performance(measure = "auc") %>% [email protected]## ]## 0.5386955

Możemy kontynuować „dostrajanie” naszych modeli, aby poprawić te wskaźniki klasyfikacji. Jeśli możesz poprawić swoje krzywe AUC i ROC (co oznacza, że poprawiasz wskaźniki dokładności klasyfikacji), tworzysz „wzrost”, co oznacza, że podnosisz dokładność klasyfikacji.

Dodatkowe zasoby

To pozwoli Ci zacząć i działać z regresją logistyczną. Należy pamiętać, że jest o wiele więcej, które można wykopać, więc następujące zasoby pomogą Ci dowiedzieć się więcej:

• An Introduction to Statistical Learning
• Applied Predictive Modeling
• Elements of Statistical Learning

.