Dependent vs Independent Events
Kilka postów temu zacząłem mówić o prawdopodobieństwach. Chcę poświęcić trochę więcej czasu na ten temat, ponieważ jest to jedna z tych koncepcji, która może być oczywiście łatwa w jednej chwili, a w następnej może być myląca.
Kiedy podchodzisz do problemu prawdopodobieństwa obejmującego więcej niż jedno zdarzenie, zacznij od zadania sobie pytania, czy zdarzenia są zależne czy niezależne, tzn. czy jedno zdarzenie zmienia prawdopodobieństwo drugiego zdarzenia? Czy pierwsze zdarzenie zmienia system?
(Wylosowanie wielu kart z talii bez wymiany jest klasycznym przykładem zdarzenia zależnego. Kiedy losujemy pierwszą kartę, system zmienia się z 52 możliwych opcji na 51, zanim nastąpi drugie zdarzenie.)
W prawdziwym życiu, ludzie mają tendencję do mylenia zależności przez cały czas. Na przykład, rzucasz uczciwą monetą. Ląduje ona na głowie 10 razy z rzędu. Jesteś pewien, że następny rzut będzie reszką…prawda?
Jakie jest prawdopodobieństwo, że następna moneta znowu będzie reszką?
Ciągle jest to 1/2. Rzucanie monetą jest zdarzeniem niezależnym. Innymi słowy, na wynik kolejnego rzutu nie ma wpływu to, co wydarzyło się wcześniej. To tak jakbyś rzucał monetą po raz pierwszy w życiu. Prawdopodobieństwo jest niezmienione.
Dlaczego „czuje się”, że to powinien być reszka wtedy?
Mamy tendencję do myślenia o wydarzeniach razem, zamiast indywidualnie. Chociaż prawdopodobieństwo wyrzucenia głowy pozostaje takie samo dla każdego rzutu, łączna szansa wyrzucenia 11 głów z rzędu jest mała.
Obliczmy to.
Nauczyliśmy się w poprzedniej lekcji prawdopodobieństwa, że kiedy łączymy wiele zdarzeń i chcemy, aby wszystkie wystąpiły (scenariusz „i”), musimy pomnożyć ich prawdopodobieństwa razem.
Ponieważ każdy rzut monetą ma prawdopodobieństwo główki równe 1/2, muszę po prostu pomnożyć razem 1/2 jedenaście razy.
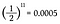
To jest 0.05% szansy na wyrzucenie jedenastu główek z rzędu! Ale zanim odetchniesz z ulgą i powiesz: „Widzisz, wiedziałem!”, obliczmy szansę na wyrzucenie ogona w jedenastym rzucie.
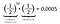
Tak, to prawda. Jest tak samo prawdopodobne, że po dziesięciu główkach nastąpi ogon, jak po jedenastu główkach z rzędu. W rzeczywistości, ponieważ indywidualne prawdopodobieństwo wyrzucenia reszki jest takie samo jak prawdopodobieństwo wyrzucenia reszki, każdy układ 11 rzutów monetą będzie miał takie samo prawdopodobieństwo wynoszące 0,0005. Każdy układ jest jednakowo prawdopodobny.
Więc… dlaczego „PRZYPADKOWO” nieprawdopodobne jest wyrzucenie dziesięciu głów z rzędu??
Powszechne błędne przekonanie nie jest spowodowane prawdopodobieństwem, ale niezrozumieniem kombinatoryki i permutacji.
Do tej pory ustaliliśmy, że:
- Prawdopodobieństwo wyrzucenia reszki lub głowy jest jednakowo prawdopodobne w każdym pojedynczym rzucie: P(H) = P(T) = 1/2.
- Każdy unikalny układ (permutacja) możliwych rzutów monetą jest równie prawdopodobny.
Więc co się dzieje?
Zrozumienie przestrzeni prób
Przestrzeń prób jest po prostu listą wszystkich możliwych układów wyników (permutacji). Ponieważ przestrzeń prób dla 11 kolejnych rzutów monetą jest dość duża, przeanalizujmy prostszy przypadek.
Przestrzeń prób dla czterech rzutów monetą wynosi:

Intuicyjnie można by pomyśleć: Bardziej prawdopodobne jest, że w czterech rzutach wypadną 2 reszki i 2 głowy niż wszystkie reszki i wszystkie głowy.
I to jest prawda. Zróbmy matematykę.
Wiemy, że każda z szesnastu permutacji jest równie prawdopodobna, ponieważ P(H) = P(T) = 1/2. Zatem każda permutacja ma równe prawdopodobieństwo:

Uwaga: Ponieważ przestrzeń próby reprezentuje wszystkie możliwe wyniki, suma wszystkich prawdopodobieństw zawsze równa się 1 (np. 0.0625 – 16 = 1).
Patrząc na naszą przestrzeń prób, ile różnych permutacji rzutu monetą prowadzi do dowolnej kombinacji 2 reszek i 2 waletów?

Zauważ, że 6 z 16 możliwych wyników daje kombinację dwa reszki i dwa głowy. Ponieważ każda z tych sześciu permutacji spełnia nasze kryteria, jest to uważane za scenariusz „lub” – więc dodaj prawdopodobieństwa razem (lub po prostu pomnóż przez 6, ponieważ wszystkie są takie same).
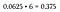
To jest 37.5% szansy na wyrzucenie kombinacji 2 głów i 2 ogonów, co jest znacznie większe niż prawdopodobieństwo wyrzucenia wszystkich głów lub wszystkich ogonów (które pozostaje 6.25% każde, ponieważ istnieje tylko jedna permutacja każdego z nich w naszej przestrzeni prób).
To dlatego intuicyjnie wiemy, że jest bardziej prawdopodobne, aby rzucić równą liczbę głów i ogonów, niż rzucić wszystkie jednego rodzaju, przy jednoczesnym zachowaniu faktu, że zdarzenia są niezależne z indywidualnymi rzutami i permutacjami równie prawdopodobne, aby wystąpić.
Permutacje &Kombinacje
Wiele z pomyślnego obliczania prawdopodobieństwa jest zrozumienie permutacji i kombinacji dokładnie. Więc to jest to, do czego zmierzamy teraz!
.