Faktoriale można znaleźć w całej kombinatoryce, ponieważ właśnie stamtąd się wywodzą. Współczynnik został stworzony jako sposób wyrażenia liczby układów grupy elementów, które oczywiście znajdujemy używając, w najbardziej podstawowej formie, zasady mnożenia w liczeniu.
Faktorial jest czymś w rodzaju nieoficjalnej operacji zasady mnożenia w liczeniu.
Why Zero Factorial Equals 1
Tutaj robi się kłopotliwie, ponieważ jeśli myślimy o współczynnikach tylko w kontekście, w którym są one zwykle definiowane, tj.tj. „iloczyn wszystkich dodatnich liczb całkowitych mniejszych lub równych tej liczbie”, wtedy zrozumienie 0! jest jak uderzenie w ścianę z cegieł.
Większość ludzi powie ci, że 0! jest zdefiniowane jako 1, a jeśli zapytasz dlaczego, po prostu powiedzą „ponieważ jest zdefiniowane jako jeden”.
Tak, to dość frustrujące. Jest to matematyczny odpowiednik pytania rodziców, dlaczego musisz przestrzegać jakiejś arbitralnej zasady, którą wymyślili, i otrzymywania odpowiedzi „bo ja tak powiedziałem”.”
Ale to może być akceptowana technika rodzicielska, ale to kiepski sposób na naukę matematyki. Więc o co chodzi? Jak zdecydowaliśmy, że zero czynnikowe równa się jeden?
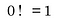
Zrozumienie intuicyjne
Pamiętasz, jak powiedzieliśmy, że czynnikowe wywodzi się z matematycznej operacji znajdowania liczby permutacji lub układów zbioru? (Uwaga: nie permutacji mniejszego zbioru z większego zbioru, ale po prostu układów danego zbioru.)
Zero factorial może być pomyślane jako liczba układów zerowych elementów w zbiorze, aka pusty zbiór {}. (Jeśli kiedykolwiek studiowałeś zestawy, być może w podstawowej statystyce lub matematyce dyskretnej, prawdopodobnie znasz pojęcie pustego zestawu. Jest to dosłownie zestaw niczego.)
Teraz, gdybym zapytał cię, ile jest aranżacji jednej rzeczy, odpowiedziałbyś 1, ponieważ istnieje tylko jeden sposób na zorganizowanie jednej rzeczy. Ta sama myśl pojawia się tutaj. Naszą „jedną rzeczą” jest zbiór pusty, a liczba układów zbioru pustego wynosi jeden. To jest to. Dlatego 0! równa się 1.
How to Simplify Factorial Expressions
Teraz, gdy mamy podstawy za sobą, nadszedł czas na serce naszego samouczka czynnikowego: upraszczanie.
Najlepszym sposobem, aby zobaczyć matematykę jest działanie. Więc oto jestem, aby poprowadzić Cię przez sześć problemów pokazanych na obrazku na górze tego posta! Zaczniemy miło i łatwo, potem przejdziemy do formuły kombinacji z liczbami i zmiennymi, a skończymy na bardziej skomplikowanych wyrażeniach czynnikowych.
❤ STAY CONNECTED ❤
Nie przegap żadnego bitu ani problemu matematycznego!