Área de um Polígono Irregular

Este artigo descreve uma solução simples para um problema geométrico, uma que eu encontro descrita de formas excessivamente complexas online. O problema é calcular a área e o comprimento do perímetro de uma figura bidimensional, fechada como a planta de uma sala, ou um terreno, ou qualquer outra figura bidimensional delimitada (um “polígono irregular”), independentemente da sua complexidade.

Não reivindico originalidade para este método. Versões já existem desde a época de Gauss ou antes. Mas a maioria dos artigos online descreve o método de formas desnecessariamente complexas. As referências incluem o artigo Wikipedia Shoelace Formula, um método similarmente complexo no artigo Polygon, e uma série de artigos que parecem calculados mais para demonstrar a erudição do autor do que para fornecer a encarnação menos complexa do método. Este artigo (PDF) mostra uma das expressões menos complexas (mas de forma alguma simples):

(1) $A = \frac{1}{2} \esquerda esquerda esquerda esquerda esquerda direita direita direita direita esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda esquerda \direita + esquerda + esquerda + barranca x_1 & x_2 y_1 & y_2}end{arranca} \direita + esquerda + esquerda + barranca x_2 & x_3 y_2 & y_3}end{arranca} \Certo… + esquerda _cc} x_{n-2} & x_{n-1} y_{n-2} & y_{n-1}end{array} \direita + esquerda + esquerda + barranca x_{n-1} & x_0 y_{n-1} & y_0}end{arranca} \direita, direita, $9367 Onde $x_n,y_n$ é um vértice polígono expresso em coordenadas cartesianas, e $esquerda, $begin{array}{cc} x_0 & x_1 {\i1}y_0 & y_1}end{array} \right|$ refere-se a um determinante, com o valor $x_0 {\i1}vezes y_1 – y_0 {\i}vezes x_1$

Não se desanime com a exposição acima – usar este método é mais fácil do que compreender os seus fundamentos matemáticos. Ao pesquisar este artigo encontrei qualquer número de respostas a perguntas de estudantes que eram tão complexas que não poderiam ter esclarecido o estudante. Neste artigo vou fazer tudo o que puder para tornar este método tão simples e acessível quanto possível.

O método é mais facilmente expresso como um algoritmo:

• Os vértices de um polígono irregular podem ser representados como coordenadas cartesianas: $x,y$.
• Cada par de coordenadas é processado num algoritmo de soma de área que se parece com isto:
  

  $A = A + \frac{(x_1 \ vezes y_0 – y_1 \ vezes x_0)}{2}$
  $A = A + \frac{(x_2 \ vezes y_1 – y_2 \ vezes x_1)}{2}$
  …

• Uma expressão matemática simples para o acima seria:
  

  (2) Área irregular do polígono $\displaystyle A = \frac{1}{2} \sum_{i=m}^{n-1}{x_{i+1} \vezes y_i – y_{i+1} \ vezes x_i}$

• NOTE: Na equação (2), a figura atravessada termina com o último item de dados fornecidos, não repete o item inicial como mostrado na equação (1) acima. Para os meus propósitos, explicados abaixo, este formulário é intencional – num levantamento do terreno os dados do campo devem fechar a figura, ou seja, o item final deve ser igual ao primeiro. Em tal aplicação, fechar automaticamente a figura como na equação (1) esconderia erros que precisam ser avaliados.

  Os usuários podem preferir o formulário mostrado na equação (1) acima, para outros propósitos que não a redução de dados do levantamento de terra. Para esses fins, durante o processamento simplesmente reëvalie o primeiro item de dados no final da travessia, ou forneça conjuntos de dados que repitam o primeiro item de dados como o último.

• Aqui está uma função Python completa e funcional:
  

  def find_area(array): a = 0 ox,oy = array para x,y no array: a += (x*oy-y*ox) ox,oy = x,y retorna a/2 

• O argumento “array” acima é um conjunto de coordenadas cartesianas $x,y$, i.e. ((10,10),(10,20),(20,20),(20,10),(10,10)). Note sobre este conjunto de dados que o primeiro item de dados é repetido no final.

• Aqui está uma função Python ligeiramente mais complexa que calcula tanto a área como o comprimento do perímetro:
  

  def find_area_perim(array): a = 0 p = 0 ox,oy = array para x,y no array: a += (x*oy-y*ox) p += abs((x-ox)+(y-oy)*1j) ox,oy = x,y retorna a/2,p 

• Again, este lembrete: para ambos os exemplos de código acima, em aplicações que não a redução de dados de levantamento da terra, o conjunto de dados fornecido deve incluir uma cópia do primeiro item de dados como o último, i.e. a figura deve ser explicitamente fechada.

• Eu escolhi Python para estes exemplos porque uma listagem Python maximiza o significado algorítmico enquanto minimiza o cruft.

• As funções acima podem ser facilmente convertidas em outras linguagens, quase diretamente – exceto a soma do perímetro mostrada acima, que explora o fato de que Python suporta números complexos. Para linguagens que não suportam números complexos, pode-se criar o resultado do perímetro desta forma:

  C/C+++: p += sqrt(pow(x-ox,2)+pow(y-oy,2));

  Java: p += Math.sqrt(Math.pow(x-ox,2)+Math.pow(y-oy,2));

• Formalmente, o comprimento do perímetro é a soma das magnitudes vectoriais:
  

  (3) Comprimento do perímetro $\displaystyle P = \sum_{i=m}^{n-1}{\sqrt{(x_{i+1}-x_i)^2 + (y_{i+1}-y_i)^2}}$

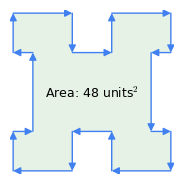
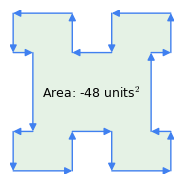Figure 1: No sentido dos ponteiros do relógio vs. vectores no sentido contrário aos ponteiros do relógio

Aqui estão algumas propriedades importantes deste método:

• O vértice de origem escolhido dentro do polígono é irrelevante para o cálculo da área ou do perímetro, apenas que a figura seja fechada, i.e. a última coordenada deve ser igual à primeira.
• “Regra Horária”: a ordem dos vetores é significativa – se o perímetro for percorrido no sentido horário, o resultado da área é positivo, se no sentido anti-horário, é negativo (Figura 1). É esta propriedade do método que subtrai a área de inflexões de uma figura complexa como na Figura 1 – as “inflexões” representam uma travessia no sentido anti-horário dentro do polígono.
• Muitas aplicações deste método usam fontes de dados originais que consistem em vetores polares (um exemplo são as descrições legais do levantamento da terra), mas este método requer coordenadas cartesianas. A conversão de coordenadas polares para cartesianas é trivial, mas é importante ter este requisito em mente.
• Again, para um cálculo de área preciso, o polígono descrito deve ser uma figura fechada – a última coordenada deve ser igual à primeira. Para aplicações que utilizam dados de campo consistindo de vetores de comprimento que são posteriormente convertidos para a forma cartesiana, é uma boa idéia comparar as coordenadas cartesianas de início e fim – elas devem ser iguais. Por exemplo, levantamentos terrestres mais antigos (antes da era de computadores baratos) falham regularmente neste teste.

Esta seção é um computador de área/perímetro totalmente funcional que pode processar pares de dados de coordenadas cartesianas ou polares inseridos, ou descrições legais de levantamentos. Basta escolher um tipo de dados (coordenadas cartesianas x,y, coordenadas polares m,θ ou uma descrição legal do levantamento) e inserir (ou colar) os dados na área de entrada de dados abaixo. Você também pode selecionar amostras de conjuntos de dados para familiarização e prática.

Por causa de problemas de segurança do navegador, para evitar digitação excessiva e para importar quantidades significativas de dados de outra fonte, os leitores precisarão usar sua área de transferência do sistema. Basta copiar os dados para a área de transferência na aplicação de origem, depois clique na área de entrada de dados abaixo e pressione Crtl+A para selecionar todos, Ctrl+V para copiar dados de outro lugar, e Ctrl+C para copiar seus próprios dados inseridos. A maioria dos navegadores também inclui funções da área de transferência como itens de menu.

Escolha o tipo de dados:

Cartesiano (x,y)

polar (m,θ)

Descrição da pesquisa

Área de entrada de dados: Selecione Tudo: Ctrl+A | Copiar: Ctrl+C | Colar: Ctrl+V

Área do gráfico:

Sorry – o seu browser não suporta a capacidade gráfica que esta funcionalidade requer –
considerar a instalação do Google Chrome ou Firefox.

Opções:

Linhas

Setas

Origem

Centro

Unidade de Comprimento:

Largura da linha:

Inverter

Resultados:Seleccionar tudo: Ctrl+A | Copiar: Ctrl+C | Colar: Ctrl+V

O computador de área/perímetro tem três modos de entrada:

• Pares de coordenadas cartesianas (x,y):

  • Cada coordenada é uma posição bidimensional com uma parte horizontal (x) e vertical (y) (uma coordenada cartesiana).
  • As coordenadas não são cumulativas – cada uma descreve independentemente a sua localização.
  • Então um quadrado seria:
    • 0,0 (origem)
    • 0,100 (para cima)
    • 100,100 (direita)
    • 100,0 (para baixo)
    • 0,0 (de volta à origem)
  >

  Figure 2: Rosa bússola

  • As vírgulas no exemplo acima destinam-se apenas a agrupar os pares de dados para o leitor – não têm qualquer significado para o analisador de dados do computador da área.
  • O analisador é suficientemente robusto para que o exemplo acima possa ser colado na área de entrada de dados do computador e funcione (tente-o).
  • A única limitação é que comentários explicativos não podem conter números.

• Polar (m,θ) pares de coordenadas:

  • Cada coordenada consiste numa distância e num ângulo em graus (um vector polar).
  • Os ângulos seguem a convenção da bússola – 0 graus é para cima ou “norte”, 90 graus é para a direita ou “leste” (Figura 2).
  • Não parecidas com a forma cartesiana anterior, estas coordenadas são cumulativas – cada novo vector adiciona à posição actual.
  • Então um quadrado seria:
    • 100,0 (acima)
    • 100,90 (direita)
    • 100,180 (abaixo)
    • 100,270 (de volta à origem)
  • Como antes, este exemplo funcionará se colado na área de entrada de dados do computador e no modo polar selecionado.
  • Nota sobre coordenadas polares que a origem está implícita e predefinida em x = 0, y = 0.
  

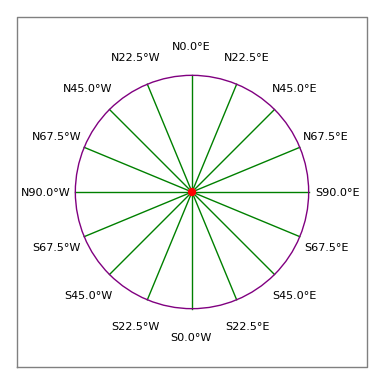  Figure 3: Bússola do agrimensor

• Descrição jurídica:

  • Primeiro, uma explicação da relação entre a selecção das “Unidades de Comprimento” e a exibição dos resultados:
    • Para cada polígono, uma lista de resultados de área é calculada usando um conjunto fixo de unidades de área comum (pés2, metros2, etc.). Para que esta lista de áreas seja significativa, as unidades de comprimento de entrada devem ser conhecidas.
    • No modo cartesiano e polar, as entradas de dados não têm unidades, portanto o usuário escolhe quais unidades atribuir aos comprimentos. Assim, quando o usuário muda as unidades de comprimento, os valores de área mudam, as etiquetas de comprimento mudam, mas os valores de comprimento não.
    • No modo Levantamento, a descrição legal contém unidades de comprimento (pés, metros, etc.) o que significa que as unidades de comprimento são predefinidas pela fonte. Assim, quando o usuário muda as unidades de comprimento, isso muda as etiquetas de comprimento e valores, não os valores de área.
  • O analisador de descrição do levantamento é de longe o menos confiável dos três métodos de análise de dados – é mais uma experiência do que um método robusto de conversão de dados.
  • Eu escrevi este analisador baixando uma série de descrições legais (que são fornecidas como exemplos na calculadora acima) e ajustando o código do analisador até que todos pudessem ser decodificados com sucesso.

  Critérios para “sucesso” eram que o resultado teria a mesma área quadrada que a descrição alega, e que a figura “fechar”.

  • O termo “fechamento”, e particularmente erro de fechamento, é usado no trabalho de levantamento para descrever o grau em que o ponto final do levantamento é igual ao ponto inicial. Isto raramente é verdade na realidade – erros de fechamento geralmente surgem de erros no trabalho de campo, e pesquisas mais antigas, publicadas antes do advento da energia barata do computador, tendem a ter fechamentos bastante ruins, bem como estimativas extremamente imprecisas de área quadrada.
  • Uma descrição legal da pesquisa é uma forma formal de descrever um terreno – sua forma e sintaxe tem surgido ao longo de décadas por convenções mutuamente aceitas, um tanto arbitrárias, compartilhadas pelos topógrafos.
  • Para este computador de área/perímetro, os dados inseridos devem seguir certas convenções rigorosas que algumas, mas não todas, as descrições legais aderem. Os elementos essenciais são:
    • A existência da frase “ponto de partida”, que separa algum conteúdo preliminar do que descreve as dimensões da parcela a ser descrita. Alguns documentos dizem “Ponto de início real”, outros dizem “Ponto de início real” e outros dizem “Ponto de início”. Um analisador bem sucedido precisa remover o conteúdo antes desta frase e reter tudo depois dela.
    • Uma série de frases que descrevem um tipo especial de vetor polar usado por topógrafos:
      • A palavra “Norte” ou “Sul”, ou a sua abreviatura “N” ou “S”.
      • Então um ângulo expresso em graus, minutos e segundos.
      • Então a palavra “Leste” ou “Oeste”, ou a sua abreviatura “E” ou “W”.
      • Então uma distância.
      • Então uma unidade de distância – pés, metros, etc.
  • Aqui estão alguns exemplos diferentes de vectores de agrimensor a partir das descrições legais da amostra:
    • N 2°0’0″ W – 63,50 pés
    • N90°00’00 “W ALONG A LINE PARALLELEL WITH SAID NORTH LINE A DISTANCE OF 6.00 FEET
    • North 0°06’O0″ West uma distância de 554.86 pés
    • S. 22 graus 41′ 55″ E. 174.10 pés
  • Nota sobre os exemplos acima que todos eles têm sintaxe diferente. Existem muitas descrições legais que este interpretador não descodifica com sucesso, apenas porque não tentei incorporar a sua sintaxe. Mas é importante acrescentar que um analisador verdadeiramente robusto para a multiplicidade de descrições legais existentes teria de ser tão inteligente como Watson.
  • Utilizadores desta área/computador de perímetro podem querer evitar submeter descrições legais em texto simples e esperar que o analisador as descodifique. Para fazer entradas manuais diretas (ou para criar uma lista de travessias em outro lugar para importação), use esta convenção:
    • Lembrar que uma entrada de travessa aceitável consiste da palavra “Norte” ou “Sul”, ou a letra “N” ou “S”, seguida de até três números fornecendo graus, minutos e segundos de ângulo, seguida da palavra “Leste” ou “Oeste” ou a letra “E” ou “W”, seguida de uma distância, seguida de uma unidade de distância.
    • Então uma entrada aceitável seria “N 30 15 45 W 100 pés”, significando uma travessia de 100 pés apontando 30 graus, 15 minutos e 45 segundos a Oeste do Norte (ou seja, cerca de 330 graus da bússola, ver Figura 3).
    • As entradas de minutos e segundos podem ser puladas se forem iguais a zero, ou se a entrada estiver em graus decimais, ou graus e minutos decimais.
  • Não é difícil converter uma descrição legal impressa em tais entradas, e há uma série de maneiras de detectar erros. Depois de todas as travessias terem sido introduzidas, se a figura não tiver erro de fecho e reportar a mesma área quadrada que a original, as hipóteses são que as entradas estejam correctas (ou que tenham os mesmos erros que a descrição original).
  • Após introduzir uma descrição legal desta forma, se houver um erro de fecho inaceitável ou se a área quadrada estiver errada, lembre-se que os dados originais podem estar errados. Há qualquer número de descrições legais existentes que nunca foram comparadas com um método de computador como este, e que nunca foram corretas.

Naqueles exemplos em cartesiano (x,y), observe a razão entre área e perímetro das diferentes formas. O “polígono de forma estranha” tem uma razão intermediária, o círculo tem a menor razão, e o espaço Hilbert tem de longe a maior razão. Esta relação estende-se a dimensões mais elevadas, onde uma esfera é conhecida por ter o maior volume por área de superfície.

Sobre o exemplo da circunferência – é uma “unidade de circunferência”, uma circunferência com um raio de uma. Para o exemplo fornecido, a área aproxima-se de $\pi$ e o perímetro aproxima-se de $2\pi$, os valores certos para uma circunferência unitária. Para que esses valores sejam mais do que aproximações, para ser exatamente igual a $\pi$ e $2\pi$, o número de lados polígonos teria que ser infinito. Eu decidi contra isto. 🙂

O exemplo espacial Hilbert foi gerado usando um algoritmo Sage com uma escolha de ordem modesta (para evitar gerar demasiados dados). Em princípio um espaço Hilbert pode ter uma relação infinita de perímetro para área em duas dimensões, ou área de superfície para volume em três dimensões. Para ver o quão complexo um espaço Hilbert pode se tornar, clique aqui para ver uma ordem-7 espaço Hilbert.

Notificação sobre o exemplo de Hilbert que a área computada está próxima de 1/2 para uma superfície 1×1. Idealmente, sem a necessidade de converter uma figura de linha em uma figura de área e com o algoritmo correto, a área de superfície seria exatamente 1/2 a de um quadrado das mesmas dimensões.

O modo de entrada polar é mais ou menos igual ao gráfico Turtle, se um substitui zero graus por “up”, 90 graus por “right”, etc., e se cada seqüência de giro e movimento é colapsada em um comando. Usando o modo de entrada polar é uma maneira fácil de construir à mão uma forma complexa, porque as distâncias e ângulos são mais fáceis de acompanhar do que as coordenadas cartesianas.

Utilizei pela primeira vez o método de computação da área de levantamento da terra descrito acima anos atrás, quando vivi na zona rural do Oregon, rodeado por pessoas que precisavam conhecer a área e o perímetro de suas propriedades. Encontrei muitos exemplos chocantes onde agentes imobiliários enganavam descaradamente pessoas que não tinham como descobrir o que estava a acontecer. Em várias ocasiões eu calculava uma área a partir de uma descrição legal, apenas para descobrir que a reivindicação da garantia sobre a área era extremamente imprecisa – e sempre superior à realidade.

Numa ocasião me pediram para dividir uma propriedade em duas seções iguais e criar descrições legais para cada uma. Como eu tinha um Apple II recentemente adquirido (que tinha o poder de processamento de um apara-lápis moderno), isso foi muito fácil – mas enquanto trabalhava eu percebi que a área total estava fora de uso por cerca de três acres, cerca de 25% do total. Eu confrontei a empresa de títulos, que descaradamente respondeu: “Veja aqui, onde a escritura diz ‘mais ou menos’?”

Em outra ocasião eu comecei a comprar um terreno, mas avisado pela experiência acima, quando recebi a política de títulos, decidi inserir sua descrição legal no meu programa para ver se a reivindicação da área estava correta. Mas para meu horror, descobri que todas as apólices de títulos para as parcelas naquela seção tinham a mesma descrição legal – da primeira propriedade pesquisada. Acontece que a empresa de desenvolvimento do terreno decidiu poupar dinheiro pesquisando apenas uma das dezenas de lotes oferecidos para venda, e incluir essa descrição legal em todas as apólices de títulos de propriedade. Eles estavam certos de que se safariam – afinal, quem sabe alguma coisa de matemática?

Depois de discutir com a companhia de títulos e o incorporador, tentando convencê-los a pagar pelas pesquisas para que as descrições legais não fossem ficções educadas, eu desisti e decidi não comprar o terreno. Foi como descobrir como é feita a salsicha – é possível saber demais.

• 04.15.2013 Versão 1.3. Adicionada uma explicação detalhada do formato de dados padrão, ou seja, listas que repetem o primeiro ponto de dados como o último.
• 03.24.2013 Versão 1.2. Optimizou ainda mais o analisador de descrição da pesquisa, adicionou mais campos de dados de resultados.
• 03.23.2013 Versão 1.1. Melhorou o analisador de descrição legal para lidar com mais tipos de descrições, adicionou seletor de unidades de comprimento e uma lista de resultados de áreas em unidades comuns.
• 03.22.2013 Versão 1.0. Versão Pública Inicial.