Equações de SHM
Considerar um bloco preso a uma mola em uma tabela sem fricção (Figura \PageIndex{3}). A posição de equilíbrio (a posição onde a mola não é esticada ou comprimida) é marcada como x = 0 . Na posição de equilíbrio, a força líquida é zero.
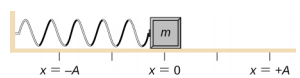
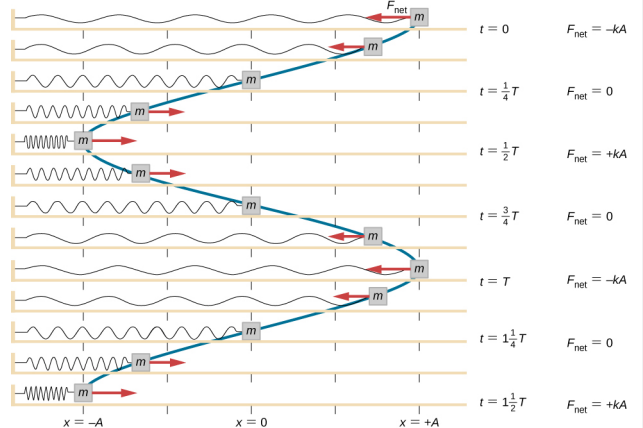
Trabalho é feito no bloco para puxá-lo para uma posição de x = + A, e depois é liberado do repouso. A posição x máxima (A) é chamada a amplitude do movimento. O bloco começa a oscilar em SHM entre x = + A e x = -A, onde A é a amplitude do movimento e T é o período da oscilação. O período é o tempo para uma oscilação. A figura \(\PageIndex{4}) mostra o movimento do bloco ao completar uma oscilação e meia após a liberação.
\
A equação para a posição em função do tempo \(x(t) = A\cos( \omega t)\) é boa para modelar os dados, onde a posição do bloco no tempo inicial t = 0,00 s está na amplitude A e a velocidade inicial é zero. Muitas vezes quando se tomam dados experimentais, a posição da massa no tempo inicial t = 0,00 s não é igual à amplitude e a velocidade inicial não é zero. Considere 10 segundos de dados coletados por um aluno em laboratório, mostrados na Figura \PageIndex (6).
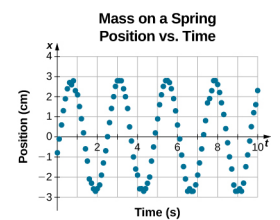
Os dados da Figura \PageIndex (6) ainda podem ser modelados com uma função periódica, como uma função co-seno, mas a função é deslocada para a direita. Este deslocamento é conhecido como deslocamento de fase e é normalmente representado pela letra grega phi (phi)). A equação da posição em função do tempo para um bloco em uma mola passa a ser de 7814>
Esta é a equação generalizada para SHM onde t é o tempo medido em segundos, {mega} é a freqüência angular com unidades de segundos inversos, A é a amplitude medida em metros ou centímetros, e {phi} é o deslocamento de fase medido em radianos (Figura 7). Deve-se notar que como as funções seno e co-seno diferem apenas por um deslocamento de fase, este movimento pode ser modelado usando a função co-seno ou seno.
A velocidade da massa em uma mola, oscilando em SHM, pode ser encontrada tomando a derivada da equação de posição:
Porque a função seno oscila entre -1 e +1, a velocidade máxima é a amplitude vezes a freqüência angular, vmax = A\(\omega). A velocidade máxima ocorre na posição de equilíbrio (x = 0) quando a massa está se movendo para x = + A. A velocidade máxima na direção negativa é atingida na posição de equilíbrio (x = 0) quando a massa está se movendo para x = -A e é igual a -vmax.
A aceleração da massa na mola pode ser encontrada tomando a derivada do tempo da velocidade: