Acontecimentos Dependentes vs Independentes
>
>
>
>>367421>>
>
>
>>367421>>
>
>
>
>>
>
Um par de posts atrás eu comecei a falar sobre probabilidades. Eu quero gastar mais algum tempo no tópico porque é um daqueles conceitos que pode ser obviamente fácil em um minuto e para baixo, confundindo o próximo.
Quando você aborda um problema de probabilidade envolvendo mais de um evento, comece perguntando-se se os eventos são dependentes ou independentes, ou seja, será que um evento altera a probabilidade do outro evento? O primeiro evento a acontecer altera o sistema?
(Tirar várias cartas de um baralho sem substituição é um exemplo clássico de um evento dependente. Quando tiramos a primeira carta o sistema muda de 52 opções possíveis para 51 antes do segundo evento acontecer.)
Na vida real, os humanos têm a tendência de confundir dependência o tempo todo. Por exemplo, você vira uma moeda justa. Aterra cabeças 10 vezes seguidas. Tens a certeza que a próxima vez que se atirar uma moeda ao ar é para ser coroa…certo?
Quais são as hipóteses da próxima moeda voltar a ser cabeça?
Ainda é 1/2. Atirar uma moeda ao ar é um evento independente. Em outras palavras, o resultado da próxima virada não é influenciado pelo que aconteceu anteriormente. É como se fosse a primeira vez que você atirou a moeda ao ar. A probabilidade é inalterada.
Porquê “sentir” como se fosse cauda então?
Tendemos a pensar nos eventos em conjunto, em vez de individualmente. Embora a probabilidade de arremessar cabeças permaneça a mesma para cada arremesso, a probabilidade combinada de arremessar 11 cabeças seguidas é pequena.
Vamos calculá-la.
Aprendemos na lição de probabilidade anterior que quando encadeamos múltiplos eventos juntos e queremos que todos eles ocorram (o cenário “e”) devemos multiplicar as suas probabilidades em conjunto.
Desde que cada lançamento de moeda tem uma probabilidade de cabeças igual a 1/2, eu simplesmente preciso multiplicar juntos 1/2 onze vezes.
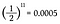
É uma probabilidade de 0,05% de virar onze cabeças seguidas! Mas antes de exalar de suspiro de alívio e dizer: “Veja, eu sabia!”, vamos calcular a chance de conseguir uma cauda no décimo primeiro arremesso.
>
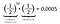
>>
>
>
Sim, é isso mesmo. É igualmente provável que se virem dez cabeças seguidas por uma cauda, como é provável que se virem onze cabeças seguidas. De fato, como a probabilidade individual de virar cabeças é a mesma que a probabilidade de virar caudas, cada arranjo de 11 moedas jogadas resultará na mesma probabilidade de 0,0005. Cada arranjo é igualmente provável.
Então… porque é que é “FEEL” improvável virar dez cabeças numa fila??
A concepção errada comum não é causada pela probabilidade, mas por um mal entendido de combinações e permutações.
Até agora estabelecemos que:
- A probabilidade de virar cabeças ou caudas é igualmente provável em cada jogada individual: P(H) = P(T) = 1/2.
- Cada disposição única (permutação) de possíveis lançamentos de moedas é igualmente provável.
O que dá?
Espaço de amostra compreensível
O espaço de amostra é simplesmente uma listagem de todos os possíveis arranjos de resultados (permutações). Uma vez que o espaço de amostra para 11 lançamentos consecutivos de moedas é bastante grande, vamos examinar antes um caso mais simples.
O espaço de amostra para quatro lançamentos de moedas é:
 >
>
Intuitivamente, podemos pensar: É mais provável que se virem 2 cabeças e 2 caudas de quatro lançamentos do que todas as cabeças ou todas as caudas.
E isto é verdade. Vamos fazer as contas.
Sabemos que cada uma das dezesseis permutações é igualmente provável porque P(H) = P(T) = 1/2. Então cada permutação tem uma probabilidade igual de:

Nota: Como o espaço de amostra representa todos os resultados possíveis, a soma de todas as probabilidades é sempre igual a 1 (ex. 0,0625 – 16 = 1).
>
Locando o nosso espaço de amostra, quantas diferentes permutações de moedas resultam em qualquer combinação 0f 2 cabeças e 2 caudas?
 >
>>>
>
Note que 6 dos 16 resultados possíveis resultam numa combinação de duas cabeças/duas caudas. Como qualquer uma dessas seis permutações atende aos nossos critérios, isso é considerado um cenário “ou” – então acrescente as probabilidades juntas (ou simplesmente multiplique por 6, já que são todas iguais).
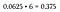
Esta é uma probabilidade de 37,5% de atirar uma combinação de 2 cabeças e 2 caudas, que é muito maior do que a probabilidade de atirar todas as cabeças ou todas as caudas (que permanece 6.25% cada uma, uma vez que há apenas uma permutação de cada um em nosso espaço de amostra).
É por isso que sabemos intuitivamente que é mais provável que se vire um número igual de cabeças e rabos, do que se vire todos de um tipo, mantendo o fato de que os eventos são independentes com os lançamentos individuais e permutações igualmente prováveis de ocorrer.
Permutações & Combinações
Muitas probabilidades de computar com sucesso é compreender bem as permutações e combinações. Então é para lá que nos dirigimos a seguir!