Logistic Regression

Regressão logística (aka logit regression ou logit model) foi desenvolvido pelo estatístico David Cox em 1958 e é um modelo de regressão onde a variável de resposta Y é categórica. A regressão logística nos permite estimar a probabilidade de uma resposta categórica baseada em uma ou mais variáveis preditoras (X). Ela permite dizer que a presença de um preditor aumenta (ou diminui) a probabilidade de um determinado resultado em uma porcentagem específica. Este tutorial cobre o caso em que Y é binário – ou seja, onde pode tomar apenas dois valores, “0” e “1”, que representam resultados tais como passe/perda, ganho/perda, vivo/morto ou saudável/doente. Casos em que a variável dependente tem mais de duas categorias de resultados podem ser analisados com regressão logística multinomial, ou, se as múltiplas categorias forem ordenadas, em regressão logística ordinal. Entretanto, a análise discriminante tornou-se um método popular para classificação multinomial, portanto nosso próximo tutorial irá focar nessa técnica para essas instâncias.

tl;dr

Este tutorial serve como uma introdução à regressão logística e cobre1:

1. Requerimentos de replicação: O que você precisará para reproduzir a análise neste tutorial
2. Por que a regressão logística: Porquê usar regressão logística?
3. Preparando os nossos dados: Preparar nossos dados para modelagem
4. Regressão logística simples: Previsão da probabilidade de resposta Y com uma única variável preditora X
5. Regressão logística múltipla: Previsão da probabilidade de resposta Y com múltiplas variáveis preditoras
6. Avaliação do modelo & Diagnóstico: Até que ponto o modelo se ajusta aos dados? Quais os preditores que são mais importantes? As previsões são precisas?

Requisitos da replicação

Este tutorial utiliza principalmente os dados Default fornecidos pelo pacote ISLR. Este é um conjunto de dados simulado contendo informações sobre dez mil clientes, tais como se o cliente inadimplente, é um estudante, o saldo médio transportado pelo cliente e a renda do cliente. Também vamos utilizar alguns pacotes que fornecem manipulação de dados, visualização, funções de modelagem de pipeline e funções de arrumação de modelos de saída.

# Packageslibrary(tidyverse) # data manipulation and visualizationlibrary(modelr) # provides easy pipeline modeling functionslibrary(broom) # helps to tidy up model outputs# Load data (default <- as_tibble(ISLR::Default))## # A tibble: 10,000 × 4## default student balance income## <fctr> <fctr> <dbl> <dbl>## 1 No No 729.5265 44361.625## 2 No Yes 817.1804 12106.135## 3 No No 1073.5492 31767.139## 4 No No 529.2506 35704.494## 5 No No 785.6559 38463.496## 6 No Yes 919.5885 7491.559## 7 No No 825.5133 24905.227## 8 No Yes 808.6675 17600.451## 9 No No 1161.0579 37468.529## 10 No No 0.0000 29275.268## # ... with 9,990 more rows

Porquê a Regressão Logística

Regressão linear não é apropriada no caso de uma resposta qualitativa. Por que não? Suponha que estamos tentando prever a condição médica de uma paciente no pronto-socorro com base nos seus sintomas. Neste exemplo simplificado, há três diagnósticos possíveis: acidente vascular cerebral, overdose de drogas e ataque epiléptico. Poderíamos considerar a codificação destes valores como uma variável de resposta quantitativa, Y , como segue:

Usando esta codificação, os mínimos quadrados poderiam ser usados para encaixar um modelo de regressão linear para prever Y com base em um conjunto de preditores . Infelizmente, esta codificação implica uma ordenação dos resultados, colocando a overdose entre o AVC e a crise epilética, e insistindo que a diferença entre AVC e overdose é a mesma que a diferença entre a overdose de drogas e a crise epilética. Na prática, não há nenhuma razão particular para que este seja o caso. Por exemplo, pode-se escolher uma codificação igualmente razoável,

o que implicaria uma relação totalmente diferente entre as três condições. Cada uma destas codificações produziria modelos lineares fundamentalmente diferentes que, em última análise, levariam a diferentes conjuntos de previsões nas observações de teste,

Mais relevante para os nossos dados, se estivermos a tentar classificar um cliente como inadimplente de alto risco versus inadimplente de baixo risco com base no seu equilíbrio, poderíamos usar a regressão linear; no entanto, a figura à esquerda abaixo ilustra como a regressão linear iria prever a probabilidade de inadimplência. Infelizmente, para saldos próximos de zero nós prevemos uma probabilidade negativa de inadimplência; se prevíssemos saldos muito grandes, obteríamos valores maiores que 1. Estas previsões não são sensatas, pois é claro que a verdadeira probabilidade de inadimplência, independentemente do saldo do cartão de crédito, deve cair entre 0 e 1,

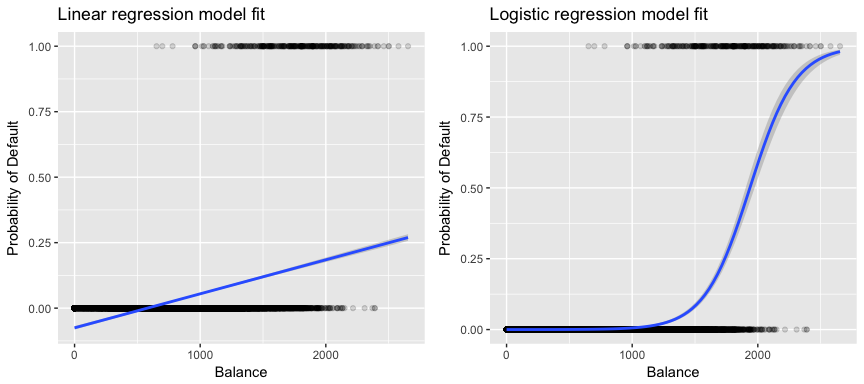
Para evitar este problema, devemos modelar p(X) usando uma função que dá saídas entre 0 e 1 para todos os valores de X. Muitas funções atendem a esta descrição. Na regressão logística, usamos a função logística, que é definida na Eq. 1 e ilustrada na figura acima.

Preparando Nossos Dados

Como no tutorial de regressão, vamos dividir nossos dados em um conjunto de dados de treinamento (60%) e teste (40%) para que possamos avaliar o desempenho do nosso modelo em um conjunto de dados fora da amostra.

set.seed(123)sample <- sample(c(TRUE, FALSE), nrow(default), replace = T, prob = c(0.6,0.4))train <- defaulttest <- default

Regressão logística simples

Apresentaremos um modelo de regressão logística de forma a prever a probabilidade de um cliente não cumprir com base no saldo médio transportado pelo cliente. A função glm encaixa em modelos lineares generalizados, uma classe de modelos que inclui a regressão logística. A sintaxe da função glm é semelhante à de lm, exceto que devemos passar o argumento family = binomial para dizer a R para executar uma regressão logística em vez de algum outro tipo de modelo linear generalizado.

model1 <- glm(default ~ balance, family = "binomial", data = train)

Em segundo plano a glm, usa a máxima probabilidade para se ajustar ao modelo. A intuição básica por trás do uso da máxima verosimilhança para encaixar um modelo de regressão logística é a seguinte: procuramos estimativas para e de tal forma que a probabilidade prevista de padrão para cada indivíduo, usando Eq. 1, corresponda o mais próximo possível do status padrão observado do indivíduo. Em outras palavras, tentamos encontrar e de tal forma que plugando essas estimativas no modelo para p(X), dado em Eq. 1, produz um número próximo a um para todos os indivíduos que não cumpriram o padrão, e um número próximo a zero para todos os indivíduos que não cumpriram. Esta intuição pode ser formalizada usando uma equação matemática chamada função de probabilidade:

As estimativas e são escolhidas para maximizar esta função de probabilidade. A probabilidade máxima é uma abordagem muito geral que é usada para se encaixar em muitos dos modelos não lineares que iremos examinar em tutoriais futuros. O que resulta é uma curva de probabilidade em forma de S ilustrada abaixo (note que para traçar a linha de ajuste da regressão logística precisamos converter nossa variável de resposta para uma variável codificada binária).

default %>% mutate(prob = ifelse(default == "Yes", 1, 0)) %>% ggplot(aes(balance, prob)) + geom_point(alpha = .15) + geom_smooth(method = "glm", method.args = list(family = "binomial")) + ggtitle("Logistic regression model fit") + xlab("Balance") + ylab("Probability of Default")

Similar à regressão linear podemos avaliar o modelo usando summary ou glance. Note que o formato de saída do coeficiente é similar ao que vimos na regressão linear; no entanto, os detalhes do goodness-of-fit no final de summary diferem. Vamos entrar nisto mais tarde, mas note que você vê a palavra desvio. Desvio é análogo à soma dos cálculos dos quadrados na regressão linear e é uma medida da falta de ajuste aos dados em um modelo de regressão logística. O desvio nulo representa a diferença entre um modelo com apenas a intercepção (que significa “sem preditores”) e um modelo saturado (um modelo com um ajuste teoricamente perfeito). O objetivo é que o desvio do modelo (notado como Desvio residual) seja menor; valores menores indicam um melhor ajuste. A este respeito, o modelo nulo fornece uma linha de base sobre a qual comparar modelos preditores.

summary(model1)## ## Call:## glm(formula = default ~ balance, family = "binomial", data = train)## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -2.2905 -0.1395 -0.0528 -0.0189 3.3346 ## ## Coefficients:## Estimate Std. Error z value Pr(>|z|) ## (Intercept) -1.101e+01 4.887e-01 -22.52 <2e-16 ***## balance 5.669e-03 2.949e-04 19.22 <2e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## (Dispersion parameter for binomial family taken to be 1)## ## Null deviance: 1723.03 on 6046 degrees of freedom## Residual deviance: 908.69 on 6045 degrees of freedom## AIC: 912.69## ## Number of Fisher Scoring iterations: 8

Coeficientes de avaliação

A tabela abaixo mostra as estimativas de coeficientes e informações relacionadas que resultam do ajuste de um modelo de regressão logística, a fim de prever a probabilidade de padrão = Sim usando o equilíbrio. Tenha em mente que as estimativas de coeficiente da regressão logística caracterizam a relação entre o preditor e a variável resposta em uma escala de log-odds (veja Ch. 3 da ISLR1 para mais detalhes). Assim, vemos que ; isto indica que um aumento no equilíbrio está associado a um aumento na probabilidade de incumprimento. Para ser preciso, um aumento do saldo de uma unidade está associado a um aumento das probabilidades logarítmicas do padrão em 0,0057 unidades.

tidy(model1)## term estimate std.error statistic p.value## 1 (Intercept) -11.006277528 0.488739437 -22.51972 2.660162e-112## 2 balance 0.005668817 0.000294946 19.21985 2.525157e-82

Podemos interpretar o coeficiente de saldo como – para cada aumento de um dólar no saldo mensal transportado, as probabilidades do cliente padrão aumentam por um fator de 1.0057.

exp(coef(model1))## (Intercept) balance ## 1.659718e-05 1.005685e+00

Muitos aspectos da saída do coeficiente são semelhantes aos discutidos na saída da regressão linear. Por exemplo, podemos medir os intervalos de confiança e a precisão das estimativas dos coeficientes através do cálculo dos seus erros padrão. Por exemplo, tem um valor de p< 2e-16 sugerindo uma relação estatisticamente significante entre o equilíbrio transportado e a probabilidade de inadimplência. Podemos também usar os erros padrão para obter intervalos de confiança como fizemos no tutorial de regressão linear:

confint(model1)## 2.5 % 97.5 %## (Intercept) -12.007610373 -10.089360652## balance 0.005111835 0.006269411

Fazer Previsões

Após os coeficientes terem sido estimados, é uma questão simples calcular a probabilidade de padrão para qualquer saldo de cartão de crédito. Matematicamente, usando as estimativas de coeficiente do nosso modelo, prevemos que a probabilidade padrão para um indivíduo com um saldo de $1.000 é inferior a 0,5%

Possibilidadede prever a probabilidade de incumprimento em R usando a função predict (certifique-se de incluir type = "response"). Aqui comparamos a probabilidade de incumprimento com base em saldos de $1000 e $2000. Como você pode ver como o saldo se move de $1000 para $2000, a probabilidade de padrão aumenta significativamente, de 0,5% para 58%!

predict(model1, data.frame(balance = c(1000, 2000)), type = "response")## 1 2 ## 0.004785057 0.582089269

A pessoa também pode usar os preditores qualitativos com o modelo de regressão logística. Como exemplo, podemos encaixar um modelo que usa a variável student.

model2 <- glm(default ~ student, family = "binomial", data = train)tidy(model2)## term estimate std.error statistic p.value## 1 (Intercept) -3.5534091 0.09336545 -38.05914 0.000000000## 2 studentYes 0.4413379 0.14927208 2.95660 0.003110511

O coeficiente associado a student = Yes é positivo, e o p-valor associado é estatisticamente significativo. Isto indica que os estudantes tendem a ter probabilidades por defeito mais elevadas do que os não estudantes. Na verdade, este modelo sugere que um aluno tem quase o dobro das probabilidades de incumprimento do que os não-alunos. Entretanto, na próxima seção veremos porque.

predict(model2, data.frame(student = factor(c("Yes", "No"))), type = "response")## 1 2 ## 0.04261206 0.02783019

Regressão logística múltipla

Podemos também estender nosso modelo como visto em Eq. 1 para que possamos prever uma resposta binária usando múltiplos preditores onde estão os preditores p:

Vamos em frente e encaixar um modelo que prevê a probabilidade de default baseado no balanço, renda (em milhares de dólares), e variáveis de status do estudante. Há um resultado surpreendente aqui. Os valores de p associados ao balanço e status do aluno=Sim são muito pequenos, indicando que cada uma dessas variáveis está associada à probabilidade de inadimplência. Entretanto, o coeficiente para a variável estudante é negativo, indicando que os estudantes têm menos probabilidade de inadimplência do que os não estudantes. Em contraste, o coeficiente para a variável aluno no modelo 2, onde prevemos a probabilidade de inadimplência com base apenas no status do aluno, indicou que os alunos têm uma maior probabilidade de inadimplência. O que dá?

model3 <- glm(default ~ balance + income + student, family = "binomial", data = train)tidy(model3)## term estimate std.error statistic p.value## 1 (Intercept) -1.090704e+01 6.480739e-01 -16.8299277 1.472817e-63## 2 balance 5.907134e-03 3.102425e-04 19.0403764 7.895817e-81## 3 income -5.012701e-06 1.078617e-05 -0.4647343 6.421217e-01## 4 studentYes -8.094789e-01 3.133150e-01 -2.5835947 9.777661e-03

O painel direito da figura abaixo fornece uma explicação para esta discrepância. As variáveis estudante e equilíbrio estão correlacionadas. Os alunos tendem a ter níveis de endividamento mais elevados, o que por sua vez está associado a uma maior probabilidade de incumprimento. Em outras palavras, os estudantes têm maior probabilidade de ter grandes saldos de cartão de crédito, que, como sabemos pelo painel esquerdo da figura abaixo, tendem a estar associados a altas taxas de inadimplência. Assim, mesmo que um estudante com um determinado saldo de cartão de crédito tenha uma menor probabilidade de inadimplência do que um não-aluno com o mesmo saldo de cartão de crédito, o fato de que os estudantes em geral tendem a ter saldos de cartão de crédito mais altos significa que, em geral, os estudantes tendem a ter uma maior probabilidade de inadimplência do que os não-alunos. Esta é uma distinção importante para uma empresa de cartão de crédito que está tentando determinar a quem eles devem oferecer crédito. Um aluno é mais arriscado que um não-aluno se não houver informação sobre o saldo do cartão de crédito do aluno. No entanto, esse estudante é menos arriscado que um não-aluno com o mesmo saldo de cartão de crédito!

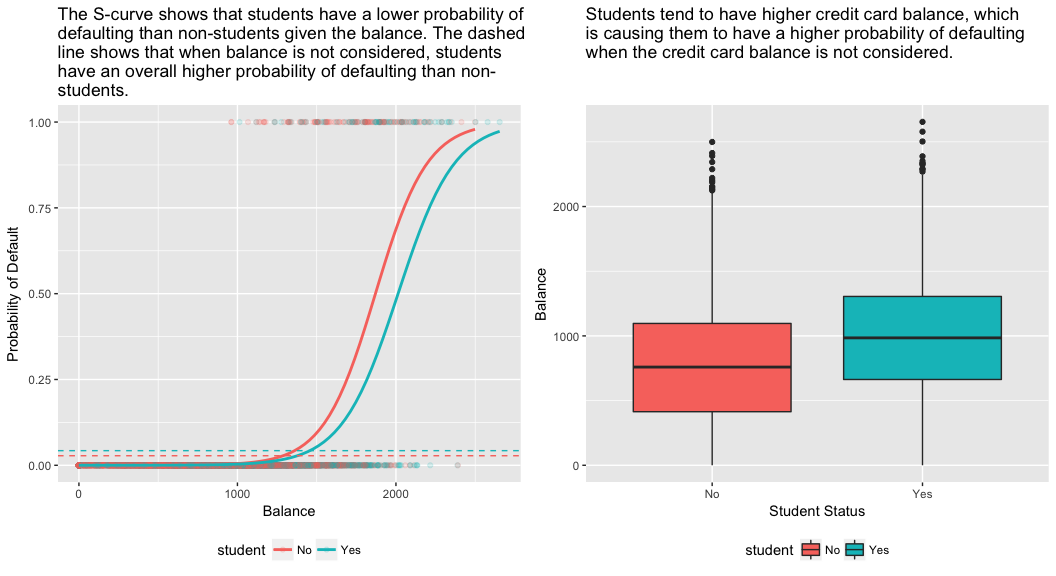
Este exemplo simples ilustra os perigos e subtilezas associadas à realização de regressões envolvendo apenas um único preditor quando outros preditores também podem ser relevantes. Os resultados obtidos usando um único preditor podem ser bastante diferentes daqueles obtidos usando múltiplos preditores, especialmente quando há correlação entre os preditores. Este fenômeno é conhecido como confuso.

No caso de variáveis de múltiplos preditores, às vezes queremos entender qual variável é a mais influente na predição da variável resposta (Y). Podemos fazer isto com varImp a partir do pacote caret. Aqui, vemos que o equilíbrio é o mais importante por uma grande margem enquanto que o estado do estudante é menos importante seguido pelo rendimento (que de qualquer forma foi considerado insignificante (p = .64)).

caret::varImp(model3)## Overall## balance 19.0403764## income 0.4647343## studentYes 2.5835947

Como antes, podemos facilmente fazer previsões com este modelo. Por exemplo, um estudante com um saldo de cartão de crédito de $1.500 e uma renda de $40.000 tem uma probabilidade estimada de padrão de

Um não-aluno com o mesmo saldo e renda tem uma probabilidade estimada de padrão de

new.df <- tibble(balance = 1500, income = 40, student = c("Yes", "No"))predict(model3, new.df, type = "response")## 1 2 ## 0.05437124 0.11440288

Assim, vemos que para o dado saldo e renda (embora a renda seja insignificante) um estudante tem cerca de metade da probabilidade de padrão do que um não-aluno.

Avaliação do modelo & Diagnóstico

Até agora foram construídos três modelos de regressão logística e os coeficientes foram examinados. No entanto, algumas questões críticas permanecem. Os modelos são bons? Até que ponto o modelo se ajusta aos dados? E quão precisas são as previsões num conjunto de dados fora da amostra?

Goodness-of-Fit

No tutorial de regressão linear vimos como a estatística F, e ajustada, e os diagnósticos residuais nos informam de quão bom o modelo se encaixa nos dados. Aqui, veremos algumas maneiras de avaliar a adequação dos nossos modelos logit.

Teste da Razão de Verossimilhança

Primeiro, podemos usar um Teste da Razão de Verossimilhança para avaliar se os nossos modelos estão melhorando a adequação. Adicionar variáveis preditoras a um modelo irá quase sempre melhorar o ajuste do modelo (ou seja, aumentar a probabilidade logarítmica e reduzir o desvio do modelo em relação ao desvio nulo), mas é necessário testar se a diferença observada no ajuste do modelo é estatisticamente significativa. Podemos usar anova para realizar este teste. Os resultados indicam que, comparado a model1, model3 reduz o desvio residual em mais de 13 (lembre-se, um objetivo da regressão logística é encontrar um modelo que minimize os residuais de desvio). Mais importante ainda, esta melhoria é estatisticamente significativa em p = 0,001. Isto sugere que model3 proporciona uma melhoria no ajuste do modelo.

anova(model1, model3, test = "Chisq")## Analysis of Deviance Table## ## Model 1: default ~ balance## Model 2: default ~ balance + income + student## Resid. Df Resid. Dev Df Deviance Pr(>Chi) ## 1 6045 908.69 ## 2 6043 895.02 2 13.668 0.001076 **## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Pseudo

Regessão linear não comparável com a estimativa dos mínimos quadrados comuns, não há estatística que explique a proporção de variância na variável dependente que é explicada pelos preditores. No entanto, há uma série de pseudo-métricas que poderiam ser de valor. A mais notável é a de McFadden , que é definida como

onde está o valor logarítmico de verossimilhança para o modelo ajustado e é a verossimilhança logarítmica para o modelo nulo com apenas uma intercepção como um preditor. A medida varia de 0 a pouco menos de 1, com valores mais próximos de zero indicando que o modelo não tem poder de previsão. Contudo, ao contrário da regressão linear, os modelos raramente atingem um McFadden elevado. Na verdade, nas próprias palavras de McFadden os modelos com um pseudo McFadden representam um ajuste muito bom. Podemos avaliar os pseudo valores de McFadden para nossos modelos com:

list(model1 = pscl::pR2(model1), model2 = pscl::pR2(model2), model3 = pscl::pR2(model3))## $model1## McFadden ## 0.4726215 ## ## $model2## McFadden ## 0.004898314 ## ## $model3## McFadden ## 0.4805543

Vemos que o modelo 2 tem um valor muito baixo, corroborando seu mau ajuste. No entanto, os modelos 1 e 3 são muito mais altos sugerindo que eles explicam uma boa quantidade de variância nos dados padrão. Além disso, vemos que o modelo 3 melhora apenas ligeiramente a sempre tão pequena.

Avaliação Residual

Cuidado que a regressão logística não assume que os resíduos são normalmente distribuídos nem que a variância é constante. No entanto, o desvio residual é útil para determinar se os pontos individuais não estão bem ajustados pelo modelo. Aqui podemos encaixar os residuais de desvio padronizados para ver quantos excedem 3 desvios padrão. Primeiro extraímos vários bits úteis dos resultados do modelo com augment e depois procedemos ao gráfico.

model1_data <- augment(model1) %>% mutate(index = 1:n())ggplot(model1_data, aes(index, .std.resid, color = default)) + geom_point(alpha = .5) + geom_ref_line(h = 3)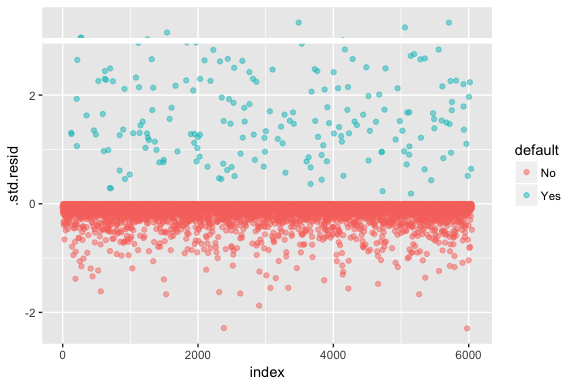

Os resíduos padronizados que excedem 3 representam possíveis outliers e podem merecer maior atenção. Podemos filtrar para que estes resíduos possam ser vistos mais de perto. Vemos que todas estas observações representam clientes que não cumprem com orçamentos muito inferiores aos normais.

model1_data %>% filter(abs(.std.resid) > 3)## default balance .fitted .se.fit .resid .hat .sigma .cooksd .std.resid index## 1 Yes 1118.7010 -4.664566 0.1752745 3.057432 0.0002841609 0.3857438 0.01508609 3.057867 271## 2 Yes 1119.0972 -4.662320 0.1751742 3.056704 0.0002844621 0.3857448 0.01506820 3.057139 272## 3 Yes 1135.0473 -4.571902 0.1711544 3.027272 0.0002967274 0.3857832 0.01435943 3.027721 1253## 4 Yes 1066.8841 -4.958307 0.1885550 3.151288 0.0002463229 0.3856189 0.01754100 3.151676 1542## 5 Yes 961.4889 -5.555773 0.2163846 3.334556 0.0001796165 0.3853639 0.02324417 3.334855 3488## 6 Yes 1143.6805 -4.522962 0.1689933 3.011233 0.0003034789 0.3858039 0.01398491 3.011690 4142## 7 Yes 1013.2169 -5.262537 0.2026075 3.245830 0.0002105772 0.3854892 0.02032614 3.246172 5058## 8 Yes 961.7327 -5.554391 0.2163192 3.334143 0.0001797543 0.3853645 0.02322988 3.334443 5709

Regessão linear semelhante à regressão linear também podemos identificar observações influentes com os valores de distância de Cook. Aqui identificamos os 5 maiores valores.

plot(model1, which = 4, id.n = 5)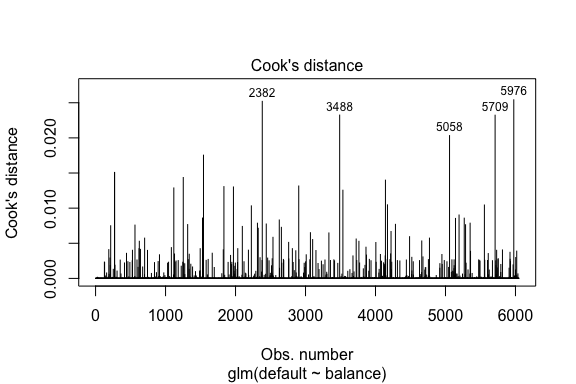

E podemos investigar estes também mais a fundo. Aqui vemos que os cinco pontos mais influentes incluem:

• os clientes que não cumpriram com os saldos muito baixos e
• dois clientes que não cumpriram com os saldos acima de $2.000

Isso significa que se removêssemos essas observações (não recomendadas), a forma, localização e intervalo de confiança da nossa regressão logística S-curva provavelmente mudaria.

model1_data %>% top_n(5, .cooksd)## default balance .fitted .se.fit .resid .hat .sigma .cooksd .std.resid index## 1 No 2388.1740 2.531843 0.2413764 -2.284011 0.0039757771 0.3866249 0.02520100 -2.288565 2382## 2 Yes 961.4889 -5.555773 0.2163846 3.334556 0.0001796165 0.3853639 0.02324417 3.334855 3488## 3 Yes 1013.2169 -5.262537 0.2026075 3.245830 0.0002105772 0.3854892 0.02032614 3.246172 5058## 4 Yes 961.7327 -5.554391 0.2163192 3.334143 0.0001797543 0.3853645 0.02322988 3.334443 5709## 5 No 2391.0077 2.547907 0.2421522 -2.290521 0.0039468742 0.3866185 0.02542145 -2.295054 5976

Validação dos valores previstos

Classificação

Ao desenvolver modelos para previsão, a métrica mais crítica é a de quão bem o modelo se sai ao prever a variável alvo nas observações fora da amostra. Primeiro, precisamos usar os modelos estimados para prever valores em nosso conjunto de dados de treinamento (train). Ao usar predict certifique-se de incluir type = response para que a previsão retorne a probabilidade de padrão.

test.predicted.m1 <- predict(model1, newdata = test, type = "response")test.predicted.m2 <- predict(model2, newdata = test, type = "response")test.predicted.m3 <- predict(model3, newdata = test, type = "response")

Agora podemos comparar a variável alvo prevista versus os valores observados para cada modelo e ver qual tem o melhor desempenho. Podemos começar usando a matriz de confusão, que é uma tabela que descreve o desempenho da classificação para cada modelo nos dados do teste. Cada quadrante da tabela tem um significado importante. Neste caso, os “Não” e “Sim” nas linhas representam se os clientes têm ou não incumprimento. Os “FALSO” e “VERDADEIRO” nas colunas representam se previmos ou não clientes por defeito.

• verdadeiros positivos (quadrante inferior direito): estes são casos em que previmos que o cliente iria por defeito e eles o fizeram.
• verdadeiros negativos (quadrante superior esquerdo): Não previmos nenhum padrão, e o cliente não previu.
• falsos positivos (quadrante superior-direita): Nós previmos que sim, mas eles não fizeram o padrão. (Também conhecido como “Tipo I de erro”)
• falso negativo (Bottom-left): Nós previmos que não, mas eles fizeram o padrão. (Também conhecido como um erro “Tipo II”)

Os resultados mostram que model1 e model3 são muito semelhantes. 96% das observações previstas são verdadeiras observações negativas e cerca de 1% são verdadeiras observações positivas. Ambos os modelos têm um erro de tipo II de menos de 3%, no qual o modelo prevê que o cliente não vai falhar, mas na verdade eles o fizeram. E ambos os modelos têm um erro de tipo I de menos de 1%, no qual o modelo prevê que o cliente não vai falhar, mas nunca falhou. model2 os resultados são notavelmente diferentes; este modelo prevê com precisão os não incumpridores (um resultado de 97% dos dados serem não incumpridores) mas nunca prevê realmente os clientes que não têm incumprimento!

list( model1 = table(test$default, test.predicted.m1 > 0.5) %>% prop.table() %>% round(3), model2 = table(test$default, test.predicted.m2 > 0.5) %>% prop.table() %>% round(3), model3 = table(test$default, test.predicted.m3 > 0.5) %>% prop.table() %>% round(3))## $model1## ## FALSE TRUE## No 0.962 0.003## Yes 0.025 0.010## ## $model2## ## FALSE## No 0.965## Yes 0.035## ## $model3## ## FALSE TRUE## No 0.963 0.003## Yes 0.026 0.009

Também queremos compreender as taxas de erro de classificação (também conhecido como erro) (ou podemos inverter isto para as taxas de precisão). Não vemos muitas melhorias entre os modelos 1 e 3 e embora o modelo 2 tenha uma baixa taxa de erro, não se esqueça que ele nunca prevê com precisão os clientes que realmente não cumprem o padrão.

>

test %>% mutate(m1.pred = ifelse(test.predicted.m1 > 0.5, "Yes", "No"), m2.pred = ifelse(test.predicted.m2 > 0.5, "Yes", "No"), m3.pred = ifelse(test.predicted.m3 > 0.5, "Yes", "No")) %>% summarise(m1.error = mean(default != m1.pred), m2.error = mean(default != m2.pred), m3.error = mean(default != m3.pred))## # A tibble: 1 × 3## m1.error m2.error m3.error## <dbl> <dbl> <dbl>## 1 0.02782697 0.03491019 0.02807994

Podemos obter algumas percepções adicionais olhando para os valores brutos (não as percentagens) em nossa matriz de confusão. Vamos olhar para o modelo 1 para ilustrar. Vemos que há um total de clientes que não cumpriram a norma. Do total de inadimplentes, não foram previstos. Alternativamente, podemos dizer que apenas das ocorrências de inadimplência foram previstas – isto é conhecido como a precisão (também conhecida como sensibilidade) do nosso modelo. Assim, enquanto a taxa de erro global é baixa, a taxa de precisão também é baixa, o que não é bom!

table(test$default, test.predicted.m1 > 0.5)## ## FALSE TRUE## No 3803 12## Yes 98 40

Com modelos de classificação você também irá aqui os termos sensitividade e especificidade ao caracterizar o desempenho do modelo. Como mencionado acima, sensibilidade é sinônimo de precisão. No entanto, a especificidade é a percentagem de não incumpridores que são correctamente identificados, aqui (a precisão aqui é em grande parte motivada pelo facto de 97% das observações nos nossos dados serem não incumpridores). A importância entre a sensibilidade e a especificidade depende do contexto. Neste caso, é provável que uma empresa de cartões de crédito esteja mais preocupada com a sensibilidade, uma vez que pretende reduzir o seu risco. Portanto, eles podem estar mais preocupados em afinar um modelo para que sua sensibilidade/precisão seja melhorada.

A característica operacional receptora (ROC) é uma medida visual do desempenho do classificador. Usando a proporção de pontos de dados positivos que são corretamente considerados como positivos e a proporção de pontos de dados negativos que são erroneamente considerados como positivos, nós geramos um gráfico que mostra o trade off entre a taxa na qual você pode predizer corretamente algo com a taxa de predição incorreta de algo. Em última análise, estamos preocupados com a área sob a curva ROC, ou AUC. Essa métrica varia de 0,50 a 1,00, e valores acima de 0,80 indicam que o modelo faz um bom trabalho na discriminação entre as duas categorias que compõem a nossa variável alvo. Podemos comparar a ROC e a AUC para os modelos 1 e 2, que mostram uma forte diferença no desempenho. Definitivamente queremos que nossos gráficos ROC se pareçam mais com os do modelo 1 (esquerda) do que com os do modelo 2 (direita)!

library(ROCR)par(mfrow=c(1, 2))prediction(test.predicted.m1, test$default) %>% performance(measure = "tpr", x.measure = "fpr") %>% plot()prediction(test.predicted.m2, test$default) %>% performance(measure = "tpr", x.measure = "fpr") %>% plot()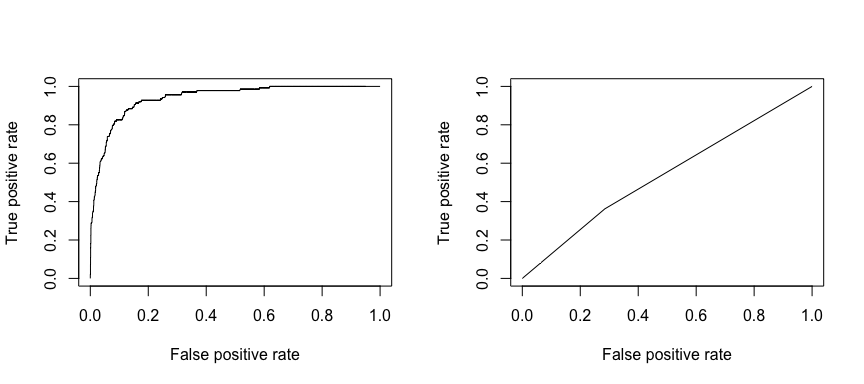

> E para calcular a AUC numericamente podemos usar o seguinte. Lembre-se, a AUC vai variar de 0,50 – 1,00. Assim, o modelo 2 é um modelo de classificação muito pobre enquanto o modelo 1 é um modelo de classificação muito bom.

# model 1 AUCprediction(test.predicted.m1, test$default) %>% performance(measure = "auc") %>% [email protected]## ]## 0.939932# model 2 AUCprediction(test.predicted.m2, test$default) %>% performance(measure = "auc") %>% [email protected]## ]## 0.5386955

Podemos continuar a “afinar” os nossos modelos para melhorar estas taxas de classificação. Se você pode melhorar suas curvas AUC e ROC (o que significa que você está melhorando as taxas de precisão de classificação) você está criando “lift”, o que significa que você está elevando a precisão de classificação.

Recursos Adicionais

Isso o colocará em funcionamento com regressão logística. Tenha em mente que há muito mais que você pode pesquisar para que os seguintes recursos o ajudem a aprender mais:

• Uma Introdução à Aprendizagem Estatística
• Aplicado Modelagem Preditiva
• Elementos de Aprendizagem Estatística