Ecuații ale SHM
Considerăm un bloc atașat de un resort pe o masă fără frecare (Figura \(\PageIndex{3}\)). Poziția de echilibru (poziția în care resortul nu este nici întins, nici comprimat) este marcată cu x = 0 . În poziția de echilibru, forța netă este zero.
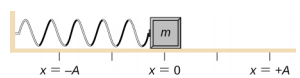
Se lucrează asupra blocului pentru a-l trage până la poziția x = + A, iar apoi acesta este eliberat din repaus. Poziția maximă x (A) se numește amplitudine a mișcării. Blocul începe să oscileze în SHM între x = + A și x = -A, unde A este amplitudinea mișcării și T este perioada de oscilație. Perioada este timpul pentru o oscilație. Figura \(\(\PageIndex{4}\) arată mișcarea blocului în timp ce acesta efectuează o oscilație și jumătate după eliberare.
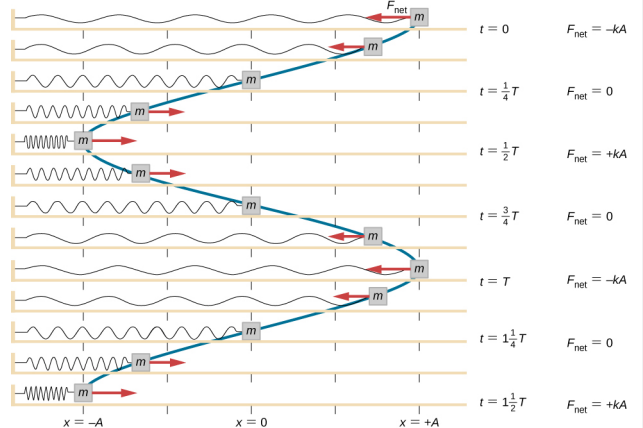
\
Ecuația pentru poziția în funcție de timp \(x(t) = A\cos( \omega t)\) este bună pentru modelarea datelor, unde poziția blocului la timpul inițial t = 0,00 s este la amplitudinea A și viteza inițială este zero. Adesea, atunci când se iau date experimentale, poziția masei la momentul inițial t = 0,00 s nu este egală cu amplitudinea și viteza inițială nu este zero. Să considerăm 10 secunde de date colectate de un student în laborator, prezentate în Figura \(\PageIndex{6}\).
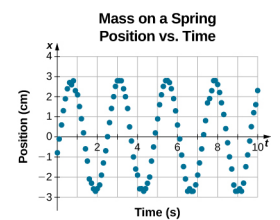
Datele din figura \(\PageIndex{6}\) pot fi în continuare modelate cu o funcție periodică, cum ar fi o funcție cosinus, dar funcția este deplasată spre dreapta. Această deplasare este cunoscută sub numele de defazaj și este reprezentată de obicei prin litera greacă phi (\(\phi\)). Ecuația poziției în funcție de timp pentru un bloc pe un resort devine
\
Aceasta este ecuația generalizată pentru SHM unde t este timpul măsurat în secunde, \(\omega\) este frecvența unghiulară cu unități de secunde inverse, A este amplitudinea măsurată în metri sau centimetri, iar \(\phi\) este defazajul măsurat în radiani (Figura \(\PageIndex{7}\)). Trebuie remarcat faptul că, deoarece funcțiile sinus și cosinus diferă doar printr-o deplasare de fază, această mișcare ar putea fi modelată folosind fie funcția cosinus, fie funcția sinus.
Viteza masei pe un resort, care oscilează în SHM, poate fi găsită luând derivata ecuației de poziție:
\
Pentru că funcția sinusoidală oscilează între -1 și +1, viteza maximă este egală cu amplitudinea înmulțită cu frecvența unghiulară, vmax = A\(\omega\). Viteza maximă apare în poziția de echilibru (x = 0) când masa se deplasează spre x = + A. Viteza maximă în sens negativ este atinsă în poziția de echilibru (x = 0) când masa se deplasează spre x = -A și este egală cu -vmax.
Accelerația masei pe resort poate fi găsită luând derivata în timp a vitezei:
\
.