Evenimente dependente vs independente
În urmă cu câteva postări am început să vorbesc despre probabilități. Vreau să dedic mai mult timp acestui subiect pentru că este unul dintre acele concepte care pot fi evident ușoare într-un minut și de-a dreptul confuze în următorul.
Când abordați o problemă de probabilitate care implică mai mult de un eveniment, începeți prin a vă întreba dacă evenimentele sunt dependente sau independente, adică dacă un eveniment modifică probabilitatea celuilalt eveniment? Întâmplarea primului eveniment schimbă sistemul?
(Extragerea mai multor cărți dintr-un pachet fără înlocuire este un exemplu clasic de eveniment dependent. Când tragem prima carte, sistemul se schimbă de la 52 de opțiuni posibile la 51 înainte ca al doilea eveniment să se întâmple.)
În viața reală, oamenii au tendința de a confunda dependența tot timpul. De exemplu, aruncați o monedă corectă. Aceasta iese cap de 10 ori la rând. Sunteți sigur că următoarea aruncare va ieși coadă…corect?
Ce șanse sunt ca următoarea monedă să iasă din nou cap?
Este tot 1/2. Aruncarea unei monede este un eveniment independent. Cu alte cuvinte, rezultatul următoarei aruncări nu este influențat de ceea ce s-a întâmplat anterior. Este ca și cum ar fi prima dată când arunci cu banul. Probabilitatea este nealterată.
De ce se „simte” că ar trebui să fie pajură atunci?
Am tendința de a ne gândi la evenimente împreună, în loc de individual. Deși probabilitatea de a arunca cap rămâne aceeași pentru fiecare aruncare, șansa combinată de a arunca 11 capete la rând este mică.
Să o calculăm.
Am învățat în lecția anterioară de probabilitate că, atunci când înșirăm mai multe evenimente împreună și dorim ca toate să se întâmple (scenariul „și”), trebuie să le înmulțim probabilitățile împreună.
Din moment ce fiecare aruncare a monedei are o probabilitate de cap egală cu 1/2, trebuie pur și simplu să înmulțesc împreună 1/2 de unsprezece ori.
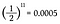
Asta este o șansă de 0,05% de a arunca unsprezece capete la rând! Dar înainte de a răsufla ușurat și de a spune: „Vezi, știam eu!”, să calculăm șansa de a obține în schimb o coadă la a unsprezecea aruncare.
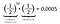
Da, așa este. Este la fel de probabil să arunci 10 capete urmate de o coadă ca și să arunci 11 capete la rând. De fapt, deoarece probabilitatea individuală de a da cu capul este aceeași cu probabilitatea de a da cu coada, fiecare aranjament de 11 aruncări ale monedei va avea ca rezultat aceeași probabilitate de 0,0005. Fiecare aranjament este la fel de probabil.
Atunci… de ce se „SIMTE” improbabil să arunci zece capete la rând?”
Concepția greșită comună nu este cauzată de probabilitate, ci de o neînțelegere a combinatoricii și a permutărilor.
Până acum am stabilit că:
- Probabilitatea de a arunca cu capul sau cu pajura este la fel de probabilă la fiecare aruncare individuală: P(H) = P(T) = 1/2.
- Care aranjament unic (permutare) al posibilelor aruncări ale monedei este la fel de probabilă.
Atunci ce se întâmplă?
Înțelegerea spațiului de eșantionare
Spațiul de eșantionare este pur și simplu o listă a tuturor aranjamentelor (permutărilor) posibile ale rezultatelor. Deoarece spațiul de eșantionare pentru 11 aruncări consecutive ale monedei este destul de mare, să examinăm în schimb un caz mai simplu.
Spațiul de eșantionare pentru patru aruncări cu banul este:

Intuitiv, am putea gândi: Este mai probabil ca din patru aruncări cu banul să iasă 2 cap și 2 pajură decât toate cap sau toate pajură.
Și acest lucru este adevărat. Să facem calculele.
Știm că fiecare dintre cele șaisprezece permutări este la fel de probabilă, deoarece P(H) = P(T) = 1/2. Deci fiecare permutare are o probabilitate egală de:

Nota: Deoarece spațiul de eșantionare reprezintă toate rezultatele posibile, suma tuturor probabilităților este întotdeauna egală cu 1 (De exemplu, 0,0625 – 16 = 1).
Urmărind spațiul nostru de eșantionare, câte permutări diferite de aruncare a monedei rezultă în orice combinație 0de 2 cap și 2 pajură?

Observați că 6 din 16 rezultate posibile au ca rezultat o combinație de 2 cap și 2 cozi. Deoarece oricare dintre aceste șase permutări îndeplinește criteriile noastre, acesta este considerat un scenariu „sau” – deci adunați probabilitățile (sau înmulțiți-le pur și simplu cu 6, deoarece toate sunt identice).
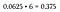
Aceasta este o șansă de 37,5% de a arunca o combinație de 2 capete și 2 pajuri, care este mult mai mare decât probabilitatea de a arunca toate capetele sau toate cozile (care rămâne 6.25% fiecare din moment ce există o singură permutare a fiecăruia în spațiul nostru de eșantionare).
De aceea știm intuitiv că este mai probabil să aruncăm un număr egal de cap și pajură, decât să le aruncăm pe toate de un singur fel, păstrând în același timp faptul că evenimentele sunt independente, cu aruncări individuale și permutări la fel de probabile.
Permutări & Combinații
O mare parte din calcularea cu succes a probabilităților constă în înțelegerea temeinică a permutărilor și combinațiilor. Așa că spre asta ne îndreptăm în continuare!
.