Aria unui poligon neregulat

Acest articol descrie o soluție simplă la o problemă geometrică, o problemă pe care o găsesc descrisă în moduri prea complexe pe internet. Problema constă în calcularea ariei și a lungimii perimetrului unei figuri bidimensionale închise, cum ar fi planul unei încăperi, sau un teren, sau orice altă figură bidimensională delimitată (un „poligon neregulat”), indiferent cât de complexă este.

Cert este că nu pretind originalitatea acestei metode. Există versiuni încă de pe vremea lui Gauss sau de dinainte. Dar majoritatea articolelor online descriu metoda în moduri inutil de complexe. Printre referințe se numără articolul Wikipedia Shoelace Formula, o metodă la fel de complexă în articolul Polygon și o serie de articole care par calculate mai mult pentru a demonstra erudiția autorului decât pentru a oferi o întruchipare cât mai puțin complexă a metodei. Acest articol (PDF) prezintă una dintre cele mai puțin complexe (dar în niciun caz simple) expresii:

(1) $A = \frac{1}{2} \left\{ \left|\begin{array}{cc} x_0 & x_1 \\\\ y_0 & y_1\\\ \end{array} \right| + \left|\begin{array}{cc} x_1 & x_2 \\\ y_1 & y_2\\ \end{array} \right| + \left|\begin{array}{cc} x_2 & x_3 \\ y_2 & y_3\\ \end{array} \right| + … + \left|\begin{array}{cc} x_{n-2} & x_{n-1} \\ y_{n-2} & y_{n-1}\\ \end{array} \right| + \left|\begin{array}{cc} x_{n-1} & x_0 \\\ y_{n-1} & y_0\\ \end{array} \right| \right\}$

Unde $x_n,y_n$ este un vârf de poligon exprimat în coordonate carteziene, iar $\left|\begin{array}{cc} x_0 & x_1 \\\ y_0 & y_1\\ \end{array} \right|$ se referă la un determinant, cu valoarea $x_0 \times y_1 – y_0 \times x_1$

Nu vă lăsați descurajați de expunerea de mai sus – utilizarea acestei metode este mai ușoară decât înțelegerea fundamentelor sale matematice. În timp ce făceam cercetări pentru acest articol am găsit un număr oarecare de răspunsuri la întrebările studenților care erau atât de complexe încât nu ar fi fost posibil să îl lumineze pe student. În acest articol voi face tot ce-mi stă în putință pentru a face această metodă cât mai simplă și mai accesibilă posibil.

Metoda este cel mai ușor de exprimat sub forma unui algoritm:

• Vârfurile unui poligon neregulat pot fi reprezentate sub formă de coordonate carteziene: $x,y$.
• Care pereche de coordonate este procesată într-un algoritm de însumare a ariei care arată astfel:
  

  $A = A + \frac{(x_1 \times y_0 – y_1 \times x_0)}{2}$
  $A = A + \frac{(x_2 \times y_1 – y_2 \times x_1)}{2}$
  …

• O expresie matematică simplă pentru cele de mai sus ar fi:
  

  (2) Aria poligonului neregulat $\displaystyle A = \frac{1}{2} \sum_{i=m}^{n-1}{x_{i+1} \times y_i – y_{i+1} \times x_i}$

• NOTA: În ecuația (2), figura traversată se termină cu ultimul element de date furnizat, nu se repetă elementul inițial, așa cum se arată în ecuația (1) de mai sus. În scopul meu, explicat mai jos, această formă este intenționată – într-un studiu de teren, datele de teren ar trebui să închidă figura, adică ultimul element ar trebui să fie egal cu primul. Într-o astfel de aplicație, închiderea automată a figurii ca în ecuația (1) ar ascunde erori care trebuie evaluate.

  Utilizatorii pot prefera forma prezentată în ecuația (1) de mai sus, în alte scopuri decât reducerea datelor de topografie. În aceste scopuri, în timpul procesării, pur și simplu reevaluați primul element de date la sfârșitul parcurgerii sau furnizați seturi de date care repetă primul element de date ca fiind ultimul.

• Iată o funcție Python completă și funcțională:
  

  def find_area(array): a = 0 ox,oy = array for x,y in array: a += (x*oy-y*ox) ox,oy = x,y return a/2 

• Argumentul „array” de mai sus este un set de coordonate carteziene $x,y$, i.e. ((10,10),(10,20),(20,20),(20,10),(10,10)). Observați despre acest set de date că primul element de date se repetă la sfârșit.

• Iată o funcție Python ceva mai complexă care calculează atât aria cât și lungimea perimetrului:
  

  def find_area_perimetru(array): a = 0 p = 0 ox,oy = array for x,y in array: a += (x*oy-y*ox) p += abs((x-ox)+(y-oy)*1j) ox,oy = x,y return a/2,p 

• Încă o dată, acest memento: pentru ambele exemple de cod de mai sus, în alte aplicații decât reducerea datelor topografice, setul de date furnizat ar trebui să includă o copie a primului element de date ca fiind ultimul, adică.e. figura ar trebui să fie închisă în mod explicit.

• Am ales Python pentru aceste exemple deoarece o listare Python maximizează semnificația algoritmică, minimizând în același timp cruft.

• Funcțiile de mai sus pot fi ușor convertite în alte limbaje, aproape direct – cu excepția însumării perimetrului prezentată mai sus, care exploatează faptul că Python suportă numere complexe. Pentru limbajele care nu suportă numere complexe, se poate crea rezultatul perimetrului în felul următor:

  C/C++: p += sqrt(pow(x-ox,2)+pow(y-oy,2));

  Java: p += Math.sqrt(Math.pow(x-ox,2)+Math.pow(y-oy,2));

• În mod formal, lungimea perimetrului este suma mărimilor vectorilor:
  

  (3) Lungimea perimetrului $\displaystyle P = \sum_{i=m}^{n-1}{\sqrt{(x_{i+1}-x_i)^2 + (y_{i+1}-y_i)^2}}}$

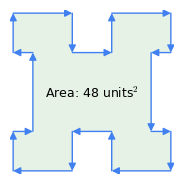
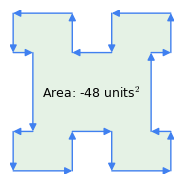Figura 1: În sensul acelor de ceasornic vs. vectori în sens invers acelor de ceasornic

Iată câteva proprietăți importante ale acestei metode:

• Vârful de origine ales în interiorul poligonului este irelevant pentru calculul ariei sau al perimetrului, ci doar ca figura să fie închisă, adică.adică ultima coordonată trebuie să fie egală cu prima.
• „Regula acelor de ceasornic”: ordinea vectorilor este semnificativă – dacă perimetrul este parcurs în sensul acelor de ceasornic, rezultatul ariei este pozitiv, dacă este în sens invers, este negativ (figura 1). Această proprietate a metodei este cea care scade aria inflexiunilor dintr-o figură complexă ca în figura 1 – „inflexiunile” reprezintă o traversare în sens invers acelor de ceasornic în interiorul poligonului.
• Multe aplicații ale acestei metode utilizează surse de date originale care constau în vectori polari (un exemplu sunt descrierile legale de topografie), dar această metodă necesită coordonate carteziene. Conversia din coordonate polare în coordonate carteziene este trivială, dar este important să se țină cont de această cerință.
• Încă o dată, pentru un calcul precis al ariei, poligonul descris trebuie să fie o figură închisă – ultima coordonată trebuie să fie egală cu prima. Pentru aplicațiile care utilizează date de teren constând în vectori de lungime care sunt convertiți ulterior în formă carteziană, este o idee bună să se compare coordonatele carteziene de început și de sfârșit – acestea ar trebui să fie egale. De exemplu, măsurătorile cadastrale mai vechi (înainte de era puterii ieftine a calculatoarelor) eșuează în mod regulat la acest test.

Această secțiune este un computer de arie/perimetru complet funcțional care poate procesa perechile de date introduse în coordonate carteziene sau polare, sau descrierile legale ale măsurătorilor. Trebuie doar să alegeți un tip de date (coordonate carteziene x,y, coordonate polare m,θ sau o descriere juridică a unui sondaj) și să introduceți (sau să lipiți) datele în zona de introducere a datelor de mai jos. De asemenea, puteți selecta seturi de date de probă pentru familiarizare și practică.

Din cauza problemelor de securitate ale browserului, pentru a evita tastarea excesivă și pentru a importa cantități semnificative de date dintr-o altă sursă, cititorii vor trebui să utilizeze clipboard-ul sistemului lor. Pur și simplu copiați datele în clipboard-ul din aplicația sursă, apoi faceți clic pe zona de introducere a datelor de mai jos și apăsați Crtl+A pentru a selecta totul, Ctrl+V pentru a pase date din altă parte și Ctrl+C pentru a copia propriile date introduse. Cele mai multe browsere includ și funcții de clipboard ca elemente de meniu.

Selectați tipul de date:

cartezian (x,y)

polar (m,θ)

Descriere survey

Data Entry Area: Selectați toate: Ctrl+A | Copy: Ctrl+C | Paste: Ctrl+V

Zona Diagramă:

Ne pare rău – browserul dvs. nu suportă capacitatea grafică pe care o necesită această funcție –
considerați instalarea Google Chrome sau Firefox.

Opțiuni:

Linii

Săgeți

Origine

Centru

Unitate de lungime:

:

Lățimea liniei:

Invers

Rezultate: Selectați toate: Ctrl+A | Copy: Ctrl+C | Paste: Ctrl+V

Computerul de suprafață/perimetru are trei moduri de intrare:

• Perechi de coordonate carteziene (x,y):

  • Care coordonată este o poziție bidimensională cu o parte orizontală (x) și una verticală (y) (o coordonată carteziană).
  • Coordonatele nu sunt cumulative – fiecare descrie independent locația sa.
  • Așa că un pătrat ar fi:
  • :
    • 0,0 (origine)
    • 0,100 (sus)
    • 100,100 (dreapta)
    • 100,0 (jos)
    • 0,0 (înapoi la origine)


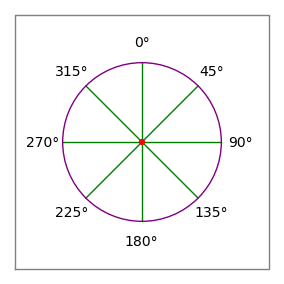Figura 2: Trandafirul busolei

• Varmele din exemplul de mai sus au doar rolul de a grupa perechile de date pentru cititor – ele nu au nicio semnificație pentru analizatorul de date al computerului de zonă.
• Parsezorul este suficient de robust pentru ca exemplul de mai sus să poată fi lipit în zona de introducere a datelor computerului și va funcționa (încercați).
• Singura limitare este că comentariile explicative nu pot conține numere.

Perechi de coordonate polare (m,θ):

• Care coordonată constă dintr-o distanță și un unghi în grade (un vector polar).
• Unghiurile urmează convenția busolei – 0 grade este în sus sau „nord”, 90 de grade este la dreapta sau „est” (figura 2).
• În mod diferit de forma carteziană anterioară, aceste coordonate sunt cumulative – fiecare nou vector se adaugă la poziția actuală.
• Așa că un pătrat ar fi:
• :
  • 100,0 (sus)
  • 100,90 (dreapta)
  • 100,180 (jos)
  • 100,270 (înapoi la origine)
• Ca și înainte, acest exemplu va funcționa dacă este lipit în zona de introducere a datelor din calculator și dacă este selectat modul polar.
• Atenție la coordonatele polare că originea este implicită și prestabilită la x = 0, y = 0.

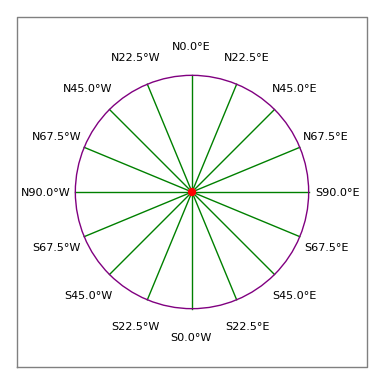Figura 3: Trandafirul busolei topografului

Descriere legală:

• În primul rând, o explicație a relației dintre selecția „Length Units” și afișarea rezultatelor:
  • Pentru fiecare poligon, se calculează o listă de rezultate de suprafață folosind un set fix de unități de suprafață comune (picioare2, metri2, etc.). Pentru ca această listă de arii să fie semnificativă, unitățile de lungime de intrare trebuie să fie cunoscute.
  • În modul cartezian și polar, intrările de date nu au unități, astfel încât utilizatorul alege ce unități să atribuie lungimilor. Astfel, atunci când utilizatorul schimbă unitățile de lungime, valorile suprafețelor se schimbă, etichetele de lungime se schimbă, dar nu și valorile lungimilor.
  • În modul Survey, descrierea legală conține unități de lungime (picioare, metri etc.), ceea ce înseamnă că unitățile de lungime sunt predefinite de sursă. Astfel, atunci când utilizatorul schimbă unitățile de lungime, acest lucru modifică etichetele și valorile de lungime, nu și valorile de suprafață.
• Analizatorul descrierii topografice este, de departe, cea mai puțin fiabilă dintre cele trei metode de analiză a datelor – este mai mult un experiment decât o metodă robustă de conversie a datelor.
• Am scris acest parser descărcând un număr de descrieri legale (care sunt furnizate ca exemple în calculatorul de mai sus) și reglând codul parserului până când toate au putut fi decodate cu succes.

Criteriile pentru „succes” au fost ca rezultatul să aibă aceeași suprafață pătrată ca și pretențiile descrierii și ca cifra să se „închidă”.

• Termenul „închidere”, și în special eroarea de închidere, este folosit în lucrările de topografie pentru a descrie gradul în care punctul final al parcurgerii topografice este egal cu punctul inițial. Acest lucru este rareori adevărat în realitate – erorile de închidere rezultă de obicei din erori în munca de teren, iar sondajele mai vechi, publicate înainte de apariția puterii ieftine a calculatoarelor, tind să aibă închideri destul de slabe, precum și estimări extrem de inexacte ale suprafeței pătrate.
• Descrierea legală a unui topograf este o modalitate formală de a descrie o parcelă de teren – forma și sintaxa sa au apărut de-a lungul deceniilor prin convenții reciproc acceptate, oarecum arbitrare, împărtășite de topografi.
• Pentru acest calculator de suprafață/perimetru, datele introduse trebuie să urmeze anumite convenții stricte la care aderă unele, dar nu toate descrierile legale. Elementele esențiale sunt:
  • Existența sintagmei „punct de început”, care separă un anumit conținut preliminar de cel care descrie dimensiunile parcelei care este descrisă. Unele documente spun „Adevăratul punct de început”, altele spun „Punctul real de început”, iar altele spun „Punctul de început”. Un parser de succes trebuie să elimine conținutul de dinaintea acestei fraze și să păstreze tot ceea ce urmează după ea.
  • O serie de fraze care descriu un tip special de vector polar folosit de topografi:
    • Cuvântul „Nord” sau „Sud”, sau abrevierea sa „N” sau „S”.
    • Apoi un unghi exprimat în grade, minute și secunde.
    • Apoi cuvântul „Est” sau „Vest”, sau abrevierea sa „E” sau „W”.
    • Apoi o distanță.
    • Apoi o unitate de măsură a distanței – picioare, metri etc.

Iată câteva exemple diferite de vectori topografici din exemplul de descrieri juridice:

• N 2°0’0″ W – 63.50 feet
• N90°00’00 „W ALONG A LINE PARALLEL WITH SAID NORTH LINE A DISTANCE OF 6.00 FEET
• North 0°06’O0″ West a distance of 554.86 picioare
• S. 22 grade 41′ 55″ E. 174.10 picioare

Atenție la exemplele de mai sus că toate au o sintaxă diferită. Există multe descrieri juridice existente pe care acest parser nu le va decoda cu succes, doar pentru că nu am încercat să le integrez sintaxa. Dar este important de adăugat că un parser cu adevărat robust pentru multitudinea de descrieri juridice existente ar trebui să fie la fel de inteligent ca Watson.

Utilizatorii acestui calculator de zonă/perimetru ar putea dori să evite să trimită descrieri juridice în text simplu și să spere că parserul își va da seama. Pentru a face intrări manuale directe (sau pentru a crea o listă de traversări în altă parte pentru import), folosiți această convenție:

• Rețineți că o intrare acceptabilă a traversării constă în cuvântul „North” sau „South”, sau litera „N” sau „S”, urmată de până la trei numere care furnizează grade, minute și secunde ale unghiului, urmate de cuvântul „East” sau „West” sau de litera „E” sau „W”, urmate de o distanță, urmată de o unitate de distanță.
• Astfel, o intrare acceptabilă ar fi „N 30 15 45 45 W 100 feet”, ceea ce înseamnă o traversare de 100 de picioare care indică 30 de grade, 15 minute și 45 de secunde la vest de nord (adică aproximativ 330 de grade compas, a se vedea figura 3).
• Înregistrările privind minutele și secundele pot fi omise dacă sunt egale cu zero sau dacă înregistrarea este în grade zecimale sau în grade și minute zecimale.

Nu este dificil să se convertească o descriere legală tipărită în astfel de înregistrări și există o serie de modalități de detectare a erorilor. După introducerea tuturor traverselor, dacă figura nu are nicio eroare de închidere și raportează aceeași suprafață pătrată ca și originalul, sunt șanse ca intrările să fie corecte (sau au aceleași erori ca și descrierea originală).

După introducerea unei descrieri legale în acest mod, dacă există o eroare de închidere inacceptabilă sau dacă suprafața pătrată este greșită, amintiți-vă că datele originale ar putea fi greșite. Există un număr oarecare de descrieri legale existente care nu au fost niciodată verificate cu o metodă computerizată ca aceasta și care nu au fost niciodată corecte.

În timp ce parcurgeți exemplele carteziene (x,y), observați raportul dintre aria și perimetrul diferitelor forme. „Poligonul cu forme ciudate” are un raport intermediar, cercul are cel mai mic raport, iar spațiul Hilbert are, de departe, cel mai mare raport. Această relație se extinde în dimensiuni mai mari, unde se știe că o sferă are cel mai mare volum pe suprafață.

În ceea ce privește exemplul cercului – este un „cerc unitar”, un cerc cu raza de unu. Pentru exemplul furnizat, aria se apropie de $\pi$ și perimetrul de $2\pi$, valori corecte pentru un cerc unitar. Pentru ca aceste valori să fie mai mult decât aproximări, pentru a fi exact egale cu $\pi$ și $2\pi$, numărul laturilor poligonului ar trebui să fie infinit. Am decis să nu fac acest lucru. 🙂

Exemplul din spațiul Hilbert a fost generat folosind un algoritm Sage cu o alegere modestă a ordinii (pentru a evita generarea a prea multe date). În principiu, un spațiu Hilbert poate avea un raport infinit între perimetru și arie în două dimensiuni, sau între suprafață și volum în trei dimensiuni. Pentru a vedea cât de complex poate deveni un spațiu Hilbert, dați clic aici pentru a vedea un spațiu Hilbert de ordinul 7.

Rețineți despre exemplul Hilbert că aria calculată este aproape de 1/2 pentru o suprafață de 1×1. În mod ideal, fără necesitatea de a converti o figură de linie într-o figură de arie și cu un algoritm corect, aria suprafeței ar fi exact 1/2 din cea a unui pătrat de aceleași dimensiuni.

Modul de introducere polară este mai mult sau mai puțin egal cu cel al graficii Turtle, dacă se înlocuiește zero grade cu „sus”, 90 de grade cu „dreapta” etc. și dacă fiecare secvență de virare și deplasare este condensată într-o singură comandă. Folosirea modului de introducere polară este o modalitate ușoară de a construi manual o formă complexă, deoarece distanțele și unghiurile sunt mai ușor de urmărit decât coordonatele carteziene.

Am folosit pentru prima dată metoda de calcul a suprafeței de topografie descrisă mai sus cu ani în urmă, când locuiam în zona rurală din Oregon, înconjurat de oameni care aveau nevoie să cunoască suprafața și perimetrul proprietăților lor. Am întâlnit multe exemple șocante în care agenții imobiliari înșelau cu nerușinare oameni care nu aveau cum să afle ce se întâmpla. În orice număr de ocazii, calculam o suprafață pornind de la o descriere legală, doar pentru a descoperi că afirmația din actul de garanție cu privire la suprafața în acri era extrem de inexactă – și întotdeauna mai mare decât în realitate.

Cu o ocazie, mi s-a cerut să împart o proprietate în două secțiuni egale și să creez descrieri legale pentru fiecare. Pentru că aveam un Apple II nou achiziționat (care avea puterea de procesare a unui ascuțitor de creioane modern), acest lucru a fost foarte ușor – dar în timp ce lucram mi-am dat seama că suprafața totală era greșită cu aproximativ trei acri, adică aproximativ 25% din total. M-am confruntat cu compania de titluri de proprietate, care mi-a răspuns cu nerușinare: „Vedeți aici, unde scrie în act „mai mult sau mai puțin”?”

Cu o altă ocazie am început o achiziție de teren, dar prevenit de experiența de mai sus, când am primit polița de titlu am decis să introduc descrierea legală a acestuia în programul meu pentru a vedea dacă afirmația privind suprafața în acri era corectă. Dar, spre groaza mea, am descoperit că toate polițele de titlu pentru parcelele din acea secțiune aveau aceeași descriere legală – a primei proprietăți măsurate. Se pare că firma de amenajare a terenurilor a decis să economisească bani prin ridicarea topografică a doar unuia dintre zecile de loturi oferite spre vânzare și să includă acea descriere legală în toate polițele de titlu. Erau siguri că vor scăpa basma curată – la urma urmei, cine se pricepe la matematică?

După cearta cu compania de titluri de proprietate și cu dezvoltatorul imobiliar, încercând să îi convingă să plătească pentru măsurători, astfel încât descrierile legale să nu fie niște ficțiuni politicoase, am renunțat și am decis să nu cumpăr terenul. A fost ca și cum aș fi aflat cum se fac cârnații – este posibil să știi prea multe.

• 04.15.2013 Versiunea 1.3. A fost adăugată o explicație detaliată a formatului de date implicit, adică liste care repetă primul punct de date ca fiind ultimul.
• 03.24.2013 Versiunea 1.2. A optimizat în continuare parserul de descriere a sondajelor, a adăugat mai multe câmpuri de date de rezultat.
• 03.23.2013 Versiunea 1.1. Îmbunătățit parserul descrierii juridice pentru a trata mai multe tipuri de descrieri, adăugat selector de unități de lungime și o listă de rezultate a suprafețelor în unități comune.
• 03.22.2013 Versiunea 1.0. Versiunea publică inițială.

.