În articolul de astăzi, veți afla care este diferența dintre numerele prime și numerele compuse. În plus, vă vom arăta câteva exemple pentru a vă ajuta să le înțelegeți mai bine.
Index
Ce sunt numerele prime?
Numerele prime sunt acele numere care sunt divizibile numai cu ele însele și cu 1, cu alte cuvinte, dacă încercăm să le împărțim cu un alt număr, rezultatul nu este un număr întreg. Deci, dacă împărțim numărul cu orice altceva în afară de 1 sau de el însuși, vom obține un rest care nu este zero.
Numere prime până la 100
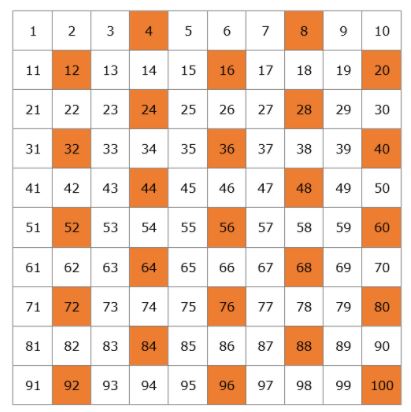
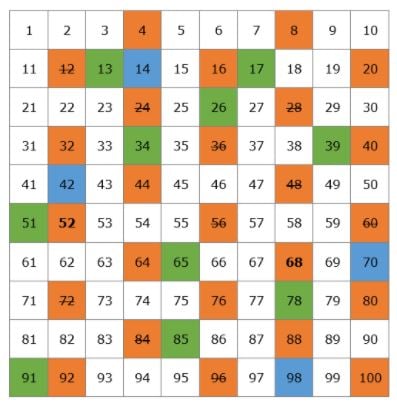
Vom crea un tabel cu toate numerele prime care există până la 100.
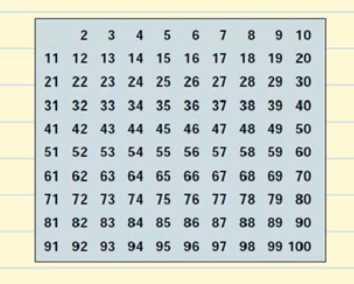
Să începem cu 2. 2 este un număr prim, dar toți multiplii lui 2 vor fi numere compuse, deoarece vor fi divizibile cu 2. Tăiem toți multiplii lui 2 din tabel.
Următorul număr prim este 3, deci putem tăia toți multiplii lui 3, deoarece vor fi numere compuse.
După 3, este următorul număr prim 5, așa că tăiem toți multiplii lui 5.
Apoi avem numărul prim 7 și tăiem toți multiplii lui 7.
Următorul număr prim este 11, așa că tăiem toți multiplii lui 11 care sunt 22, 33, 44, 55, 66, 77, 88 și 99. Toate aceste numere fuseseră deja tăiate, așa că am terminat de tăiat toate numerele compuse de pe tabelul nostru.

Aceasta este lista noastră de numere prime de la 1 la 100. Nu trebuie să le memorați, dar cel mai bine ar fi să vă amintiți numerele mai mici, cum ar fi 2, 3, 5, 7, 11, 13.
Câte numere prime există?
Matematicianul grec Eratostene (secolul al III-lea î.Hr.) a conceput o modalitate rapidă de a găsi toate numerele prime până la orice număr dat. Este un procedeu numit Sita lui Eratostene.
Rețineți că între 1 și 100 există 25 de numere prime. Câte numere prime există în total? Știm din cele mai vechi timpuri că există o cantitate infinită, deci este imposibil să le enumerăm pe toate. Deoarece Euclid, care a fost primul care a demonstrat că există o cantitate infinită în secolul al IV-lea î.Hr. nu cunoștea conceptul de infinit, el a spus că „numerele prime sunt mai multe decât orice mulțime fixă de numere prime”, ceea ce înseamnă că dacă vă imaginați 100, sunt mai multe, iar dacă vă imaginați un milion, sunt tot mai multe.
Numere prime de la 100 la 1.000
Să aruncăm o privire la numerele prime de la 100 la 1.000.

Ne pare rău că nu le putem arăta pe toate, deoarece știți că există o cantitate infinită. 😉
Exemple de numere prime
Pentru a vă ajuta să înțelegeți mai bine numerele prime, vă vom explica un exercițiu.
Sara are 6 bomboane de ciocolată pe care vrea să le împartă, dar nu știe cu câte persoane le poate împărți astfel încât toată lumea să primească aceeași cantitate și să nu rămână niciuna în plus. În câte moduri poate face acest lucru?
Iată-o pe Sara și cele 6 bomboane:

Cum le putem împărți?
Prima și cea mai ușoară modalitate este să le dăm unei singure persoane, cu alte cuvinte, să le împărțim la 1. În acest fel, acea persoană va avea 6 bomboane.
Următoarea posibilitate este să le împărțim între 2 persoane. Deoarece 6 împărțit la 2 este 3, fiecare persoană primește 3 bomboane!

Vom continua cu următorul număr, 3. Dacă împărțim 6 bomboane între 3 persoane, este tot o împărțire exactă și fiecare persoană va primi 2 bomboane:

Să continuăm cu numerele. Nu avem diviziuni exacte cu 4 și 5, dar avem cu 6.
Din moment ce 6 împărțit la 6 este 1, putem da la 6 copii câte o bomboană de fiecare.

Vom colecta câteva informații. Avem 6 bomboane pe care le putem împărți (cu o împărțire exactă) între 1, 2, 3 și 6 persoane. Cu alte cuvinte, putem să împărțim numărul 6 și să obținem 0 ca rest atunci când îl împărțim la 1, 2, 3 și 6. Aceste numere sunt cunoscute sub numele de divizorii lui 6.
Vom încerca cu un alt număr, 7 de exemplu.
Acum Sara are 7 bomboane și vrea să le împartă, dar nu știe cu câte persoane le poate împărți astfel încât toată lumea să primească aceeași cantitate și să nu rămână niciuna. În câte moduri poate face acest lucru?

Henry este atât de norocos! A primit toate bucățile de bomboane!
Există și alte moduri de a face acest lucru? Nu putem împărți 7 la 2, 3, 4, 5 sau 6, …dar 7 este posibil!
Sara poate împărți bomboanele între 7 persoane, dându-le câte o bomboană fiecăruia:

Atunci 7 poate fi împărțit doar la 1 și 7, singurii săi divizori sunt 1 și 7. Acestea sunt tipurile de numere pe care le numim numere prime.
Există mai multe numere prime? Bineînțeles că da! Să mai căutăm câteva:
- Este 4? Nu! Pentru că divizorii săi sunt 1, 2 și 4.
- Este 5? Da! Pentru că divizorii săi sunt 1 și 5.
- Este 8? Nu! Pentru că divizorii săi sunt 1, 2, 4 și 8.
În concluzie, un număr este prim dacă are doar 2 divizori: 1 și el însuși.
Acum puteți căuta o mulțime de numere prime!
Cum se găsesc numerele prime
Atenție mare! Vă vom da un truc pentru a ști dacă un număr este prim sau nu, fără a fi nevoie să căutăm divizorii săi, ci într-un mod mai distractiv și care ne oferă divizorii (dacă îi are).
Să alegem un număr la întâmplare, 16 de exemplu.
Pentru a verifica dacă este un număr prim sau nu, vom folosi un tabel foarte asemănător cu cel al cărților Montessori pentru înmulțire. Și vom avea atâtea bile cât numărul pe care l-am ales. În acest caz, 16 bile.
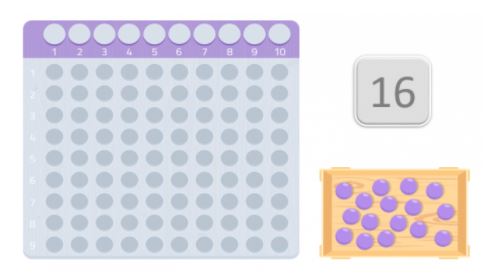
După ce avem tabelul și bilele, trebuie să le așezăm pe masă începând cu primul spațiu, încercând să formăm un dreptunghi. Numerele care alcătuiesc marginile dreptunghiului sunt divizorii acelui număr.
În cazul în care reușim să formăm un dreptunghi doar cu același număr pe care îl folosim și cu numărul 1, acesta va fi un număr prim.
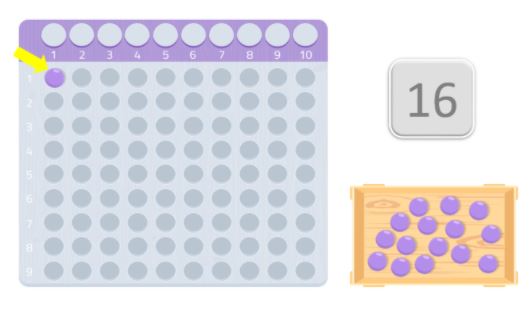
De exemplu, în acest caz, punem 8 bile în primul rând și alte 8 în al doilea rând. După cum vedeți, am format un dreptunghi și putem observa că 8, ca și 2, sunt divizori ai numărului 16. Prin urmare, 16 nu este un număr prim, deoarece, după cum știți, numerele prime sunt cele care sunt divizibile numai cu ele însele și cu 1.
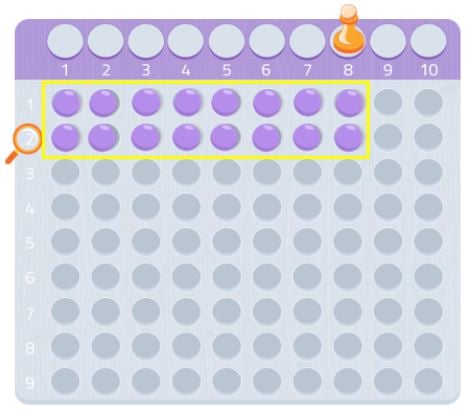
Potem încerca cu un alt număr, de exemplu 7.
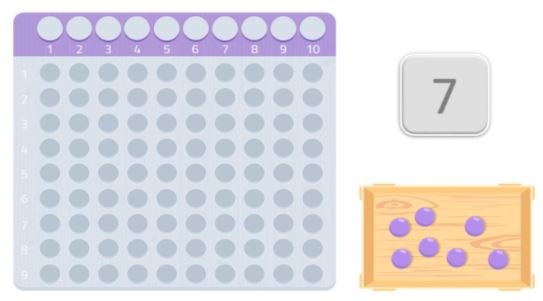
Cum vedem, nu am putea face un dreptunghi întreg, ne-ar lipsi o bilă. Din moment ce nu putem forma un dreptunghi, am putea spune că numărul 7 nu are alți divizori în afară de el însuși și de 1, așa cum putem vedea în imaginea următoare.
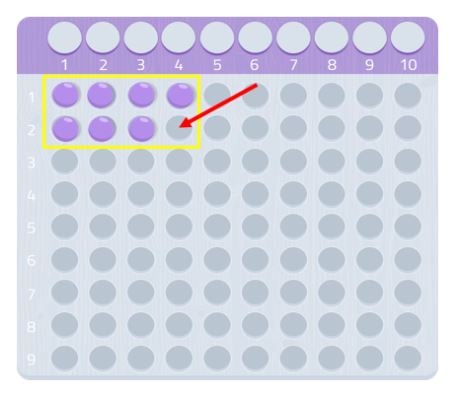
Din acest motiv, 7 este un număr prim!
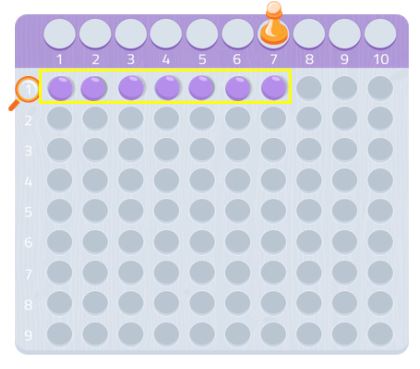
Încercați cu orice alt număr, veți vedea cum funcționează! Poți să folosești hârtie grafică și să cauți dreptunghiuri folosind acel număr de pătrate.
De ce sunt importante numerele prime?
Numerele prime sunt cheia aritmeticii, mai jos veți vedea un exemplu care demonstrează importanța lor, nu doar în matematică, ci și în natură.
Ce vrem să spunem când spunem că numerele prime sunt cheia aritmeticii?
Aceasta se datorează faptului că orice număr este format dintr-un produs unic alcătuit dintr-o serie de astfel de numere.
Se crede că ele sunt studiate de aproximativ 20.000 de ani, când un strămoș al nostru a notat o serie de numere prime (11, 13, 17 și 19) pe osul Ishango. Ca și cum ar fi fost o coincidență, s-a confirmat că vechii egipteni lucrau cu ele în urmă cu 4.000 de ani.
În plus, natura le cunoaște foarte bine și unele specii au reușit să le descopere de-a lungul evoluției lor și să profite de ele pentru a supraviețui.
Mă refer la mai multe specii de cicade, cum ar fi Magicicada septendecium care trăiește în America de Nord. Această specie de cicadă și-a stabilit ciclul de reproducere în jurul a 13 sau 17 ani, nu 12, 14, 15, 16 sau 18 – exact 13 sau 17 ani. Acest lucru le permite să evite prădătorii care au, de asemenea, cicluri de reproducere periodice; imaginați-vă un prădător cu un ciclu de reproducere de 4 ani.
Dacă ciclul de viață al unei cicade ar fi de 12 sau 14 ani, aceasta ar coincide cu un prădător foarte frecvent, mult mai mult decât dacă ar fi de 13 sau 17 ani. Exact de 2 ori la 100 de ani, în timp ce, în caz contrar, ar coincide în 11 cicluri, ceea ce ar compromite dezvoltarea speciei.
Securitatea comunicațiilor electronice se bazează și ea pe numere prime. Fiecărui mesaj criptat trimis pe internet (rețele de mesaje, achiziții sau operațiuni bancare electronice) îi este asociat un număr mare și este foarte greu de știut unde este prim sau nu. Destinatarul are unul dintre divizorii săi și de aceea îl poate decripta. Așadar, a avea numere prime este esențial pentru confidențialitatea noastră atunci când comunicăm electronic.
Ce sunt numerele compuse?
Numerele compuse sunt acele numere care sunt divizibile cu 1 și cu ele însele, precum și cu alte numere.
Ne vom uita la un exemplu de număr prim și de număr compus.
11 poate fi scris ca înmulțirea 1 x 11, dar nu poate fi scris ca orice altă înmulțire a numerelor naturale. El are doar divizorii 1 și 11 și, prin urmare, este un număr prim.
12 poate fi scris ca înmulțirea 1 x 12 și ca înmulțirea 3 x 4 și 2 x 6. Deoarece 12 este divizibil cu mai multe numere decât 1 și el însuși, 12 este un număr compus.
Este 1 un număr prim?
Există oameni care cred că da, deoarece spun că 1 poate fi împărțit doar la 1 și la el însuși, dar în matematică, numărul 1 a fost eliminat ca număr prim deoarece are doar un singur divizor. De fapt, criteriul „un număr întreg pozitiv este prim dacă are exact doi divizori pozitivi” este folosit pentru a exclude numărul 1 din lista numerelor prime. Nu pentru că suntem pretențioși în această privință, dar dacă numărul unu ar fi considerat prim, atunci multe proprietăți matematice ar trebui să fie spuse altfel.
Atunci, 1 este un număr compus?
Ei bine, nici compus nu este, deoarece nu poate fi pus ca produs de numere prime. Numărul 1 nu este nici prim, nici compus. Și, înainte de a întreba, nici zero nu este prim sau compus, dar asta pentru că toate considerațiile pe care le explicam pentru numerele pozitive, adică mai mari decât zero.
Divizorii unui număr
Divizorul unui număr este valoarea care împarte numărul în părți exacte, cu alte cuvinte, are un rest 0.
Ca exemplu, vom calcula divizorii pentru 24.
Începem împărțirea cu cele mai mici numere începând cu 1.
- 24 / 1 = 24. Atât 1 cât și 24 sunt divizori.
- 24 / 2 = 12. Deci 2 și 12 sunt divizori.
- 24 / 3 = 8. Deci 3 și 8 sunt divizori.
- 24 / 4 = 6. Deci 4 și 6 sunt divizori.
- 24 / 5 = 4. Nu este o împărțire exactă și are un rest de 4, deci 5 nu este un divizor.
Următorul număr este 6, dar cum știm deja că 6 este un divizor al lui 24, am terminat de calculat divizorii pentru 24.
Video: Factorizarea și numerele prime
Dacă doriți să aflați mai multe despre numerele prime și compuse, aruncați o privire la următorul videoclip. Veți învăța, de asemenea, conceptul de factorizare prin utilizarea tabelului Montessori.
Acest videoclip este unul dintre tutorialele noastre interactive și, deși nu este interactiv, îl puteți viziona de câte ori aveți nevoie și îl puteți partaja cu prietenii. Dacă doriți să accesați tutorialele noastre interactive, înregistrați-vă la Smartick! Metoda online care îi ajută pe copiii cu vârste cuprinse între 4 și 14 ani să învețe și să exerseze matematica.
Dacă doriți să continuați să învățați despre numerele prime și cea mai bună matematică adaptată nivelului dumneavoastră, înregistrați-vă cu Smartick și încercați-o gratuit!
Învățați mai multe:
- Numerele prime și numerele compuse
- Numerele prime: Un truc pentru a vă ajuta să le identificați
- Numerele prime: Cum să le găsiți cu sita lui Eratostene
- Învățați cum să vă factorizați în numere prime
- Activități cu numere prime cu Smartick



- Autor
- Postări recente
O echipă multidisciplinară și multiculturală formată din matematicieni, învățători, profesori și alți profesioniști din domeniul educației!
Se străduiesc să creeze cel mai bun conținut de matematică posibil.
- Exemple de probleme de matematică de clasa a III-a cu soluții – 03/25/2021
- Unghiuri interioare consecutive: Ce sunt și cum se găsesc cu exemple – 03/11/2021
- Exemple de probleme de matematică de clasa a II-a cu soluții – 02/04/2021