 Regresia logistică (cunoscută și ca regresie logit sau model logit) a fost dezvoltată de statisticianul David Cox în 1958 și este un model de regresie în care variabila de răspuns Y este categorică. Regresia logistică ne permite să estimăm probabilitatea unui răspuns categoric pe baza uneia sau mai multor variabile predictive (X). Aceasta ne permite să spunem că prezența unui predictor crește (sau scade) probabilitatea unui anumit rezultat cu un anumit procent. Acest tutorial se referă la cazul în care Y este binar – adică atunci când poate lua doar două valori, „0” și „1”, care reprezintă rezultate cum ar fi „pass/fail”, „win/lose”, „alive/dead” sau „healthy/sick”. Cazurile în care variabila dependentă are mai mult de două categorii de rezultate pot fi analizate cu ajutorul regresiei logistice multinomiale sau, în cazul în care categoriile multiple sunt ordonate, cu ajutorul regresiei logistice ordinale. Cu toate acestea, analiza discriminantă a devenit o metodă populară pentru clasificarea în mai multe clase, astfel încât următorul nostru tutorial se va concentra pe această tehnică pentru aceste cazuri.
Regresia logistică (cunoscută și ca regresie logit sau model logit) a fost dezvoltată de statisticianul David Cox în 1958 și este un model de regresie în care variabila de răspuns Y este categorică. Regresia logistică ne permite să estimăm probabilitatea unui răspuns categoric pe baza uneia sau mai multor variabile predictive (X). Aceasta ne permite să spunem că prezența unui predictor crește (sau scade) probabilitatea unui anumit rezultat cu un anumit procent. Acest tutorial se referă la cazul în care Y este binar – adică atunci când poate lua doar două valori, „0” și „1”, care reprezintă rezultate cum ar fi „pass/fail”, „win/lose”, „alive/dead” sau „healthy/sick”. Cazurile în care variabila dependentă are mai mult de două categorii de rezultate pot fi analizate cu ajutorul regresiei logistice multinomiale sau, în cazul în care categoriile multiple sunt ordonate, cu ajutorul regresiei logistice ordinale. Cu toate acestea, analiza discriminantă a devenit o metodă populară pentru clasificarea în mai multe clase, astfel încât următorul nostru tutorial se va concentra pe această tehnică pentru aceste cazuri.
- tl;dr
- Cerințe de replicare
- De ce Regresia logistică
- Pregătirea datelor noastre
- Simplă regresie logistică
- Evaluarea coeficienților
- Facerea de predicții
- Regresie logistică multiplă
- Evaluarea modelului & Diagnostice
- Buna adecvare a modelului
- Testul raportului de verosimilitate
- Pseudo
- Evaluare reziduală
- Validarea valorilor prezise
- Taxa de clasificare
- Resurse suplimentare
tl;dr
Acest tutorial servește ca o introducere în regresia logistică și acoperă1:
- Cerințe de replicare: De ce veți avea nevoie pentru a reproduce analiza din acest tutorial
- De ce regresia logistică: De ce să folosim regresia logistică?
- Pregătirea datelor noastre: Pregătiți datele noastre pentru modelare
- Regresia logistică simplă: Predicția probabilității răspunsului Y cu o singură variabilă predictoare X
- Regresia logistică multiplă: Predicția probabilității răspunsului Y cu mai multe variabile predictive
- Evaluarea modelului & diagnostice: Cât de bine se potrivește modelul la date? Ce predictori sunt cei mai importanți? Sunt previziunile exacte?
Cerințe de replicare
Acest tutorial utilizează în principal datele Default furnizate de pachetul ISLR. Acesta este un set de date simulate care conține informații despre zece mii de clienți, cum ar fi dacă clientul a intrat în incapacitate de plată, dacă este student, soldul mediu purtat de client și venitul acestuia. Vom folosi, de asemenea, câteva pachete care oferă funcții de manipulare a datelor, vizualizare, funcții de modelare a conductelor și funcții de ordonare a rezultatelor modelului.
# Packageslibrary(tidyverse) # data manipulation and visualizationlibrary(modelr) # provides easy pipeline modeling functionslibrary(broom) # helps to tidy up model outputs# Load data (default <- as_tibble(ISLR::Default))## # A tibble: 10,000 × 4## default student balance income## <fctr> <fctr> <dbl> <dbl>## 1 No No 729.5265 44361.625## 2 No Yes 817.1804 12106.135## 3 No No 1073.5492 31767.139## 4 No No 529.2506 35704.494## 5 No No 785.6559 38463.496## 6 No Yes 919.5885 7491.559## 7 No No 825.5133 24905.227## 8 No Yes 808.6675 17600.451## 9 No No 1161.0579 37468.529## 10 No No 0.0000 29275.268## # ... with 9,990 more rowsDe ce Regresia logistică
Regresia liniară nu este adecvată în cazul unui răspuns calitativ. De ce nu? Să presupunem că încercăm să prezicem starea medicală a unui pacient din camera de urgență pe baza simptomelor sale. În acest exemplu simplificat, există trei diagnostice posibile: accident vascular cerebral, supradoză de medicamente și criză de epilepsie. Am putea lua în considerare codificarea acestor valori ca o variabilă de răspuns cantitativ, Y , după cum urmează:
Utilizând această codificare, se pot folosi cele mai mici pătrate pentru a ajusta un model de regresie liniară pentru a prezice Y pe baza unui set de predictori . Din nefericire, această codificare implică o ordonare a rezultatelor, plasând supradozajul de medicamente între accidentul vascular cerebral și criza epileptică și insistând asupra faptului că diferența dintre accidentul vascular cerebral și supradozajul de medicamente este aceeași cu diferența dintre supradozajul de medicamente și criza epileptică. În practică, nu există niciun motiv special pentru care acest lucru trebuie să fie așa. De exemplu, s-ar putea alege o codificare la fel de rezonabilă,
care ar implica o relație total diferită între cele trei afecțiuni. Fiecare dintre aceste codificări ar produce modele liniare fundamental diferite care, în cele din urmă, ar conduce la seturi diferite de predicții privind observațiile de testare.
Mai relevant pentru datele noastre, dacă încercăm să clasificăm un client ca fiind cu risc ridicat vs. cu risc scăzut de neplată pe baza soldului său, am putea folosi regresia liniară; cu toate acestea, figura din stânga de mai jos ilustrează modul în care regresia liniară ar prezice probabilitatea de neplată. Din nefericire, pentru solduri apropiate de zero, prezicem o probabilitate negativă de neplată; dacă am prezice pentru solduri foarte mari, am obține valori mai mari de 1. Aceste predicții nu sunt rezonabile, deoarece, desigur, probabilitatea reală de neplată, indiferent de soldul cardului de credit, trebuie să se încadreze între 0 și 1.
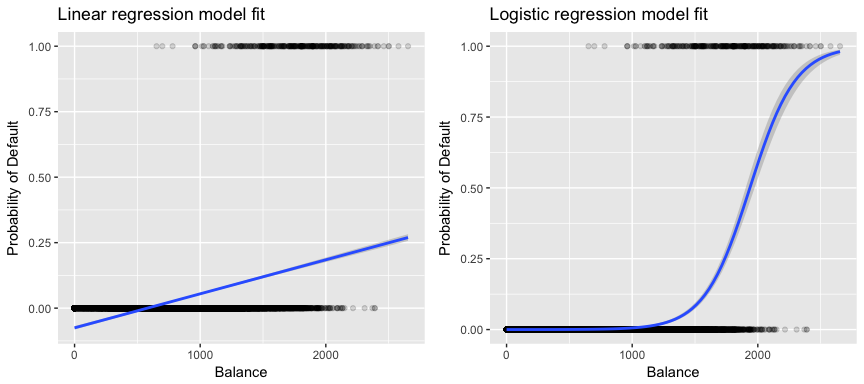
Pentru a evita această problemă, trebuie să modelăm p(X) folosind o funcție care oferă ieșiri între 0 și 1 pentru toate valorile lui X. Multe funcții îndeplinesc această descriere. În regresia logistică, folosim funcția logistică, care este definită în Ecuația 1 și ilustrată în figura din dreapta de mai sus.
Pregătirea datelor noastre
Ca și în tutorialul de regresie, vom împărți datele noastre într-un set de date de instruire (60%) și unul de testare (40%), astfel încât să putem evalua cât de bine se comportă modelul nostru pe un set de date în afara eșantionului.
set.seed(123)sample <- sample(c(TRUE, FALSE), nrow(default), replace = T, prob = c(0.6,0.4))train <- defaulttest <- defaultSimplă regresie logistică
Vom ajusta un model de regresie logistică pentru a prezice probabilitatea ca un client să intre în incapacitate de plată pe baza soldului mediu purtat de client. Funcția glm ajustează modelele liniare generalizate, o clasă de modele care include regresia logistică. Sintaxa funcției glm este similară cu cea a funcției lm, cu excepția faptului că trebuie să trecem argumentul family = binomial pentru a-i spune lui R să ruleze o regresie logistică și nu un alt tip de model liniar generalizat.
model1 <- glm(default ~ balance, family = "binomial", data = train)În fundal, funcția glm, utilizează probabilitatea maximă pentru a ajusta modelul. Intuiția de bază din spatele utilizării verosimilității maxime pentru a ajusta un model de regresie logistică este următoarea: căutăm estimări pentru și astfel încât probabilitatea prezisă de neîndeplinire a obligațiilor de plată pentru fiecare individ, utilizând Ecuația 1, să corespundă cât mai mult posibil cu starea de neîndeplinire a obligațiilor de plată observată a individului. Cu alte cuvinte, încercăm să găsim și astfel încât, dacă introducem aceste estimări în modelul pentru p(X), dat în Ecuația 1, să obținem un număr apropiat de unu pentru toate persoanele care au intrat în incapacitate de plată și un număr apropiat de zero pentru toate persoanele care nu au intrat în incapacitate de plată. Această intuiție poate fi formalizată cu ajutorul unei ecuații matematice numite funcție de verosimilitate:
Sunt alese estimările și pentru a maximiza această funcție de verosimilitate. Verosimilitudinea maximă este o abordare foarte generală care este utilizată pentru a ajusta multe dintre modelele neliniare pe care le vom examina în viitoarele tutoriale. Ceea ce rezultă este o curbă de probabilitate în formă de S, ilustrată mai jos (rețineți că pentru a trasa linia de potrivire a regresiei logistice trebuie să convertim variabila noastră de răspuns într-o variabilă cu cod binar).
default %>% mutate(prob = ifelse(default == "Yes", 1, 0)) %>% ggplot(aes(balance, prob)) + geom_point(alpha = .15) + geom_smooth(method = "glm", method.args = list(family = "binomial")) + ggtitle("Logistic regression model fit") + xlab("Balance") + ylab("Probability of Default")
Similar cu regresia liniară, putem evalua modelul folosind summary sau glance. Rețineți că formatul de ieșire a coeficienților este similar cu cel pe care l-am văzut în cazul regresiei liniare; cu toate acestea, detaliile privind bonitatea de potrivire din partea de jos a summary diferă. Vom intra mai mult în acest aspect mai târziu, dar rețineți doar că vedeți cuvântul devianță. Devianța este analogă cu calculele sumei pătratelor în regresia liniară și este o măsură a lipsei de potrivire a datelor într-un model de regresie logistică. Devianța nulă reprezintă diferența dintre un model cu doar interceptul (ceea ce înseamnă „fără predictori”) și un model saturat (un model cu o potrivire teoretic perfectă). Obiectivul este ca devianța modelului (notată ca devianță reziduală) să fie mai mică; valorile mai mici indică o potrivire mai bună. În acest sens, modelul nul oferă o linie de bază pe baza căreia se compară modelele predictorilor.
summary(model1)## ## Call:## glm(formula = default ~ balance, family = "binomial", data = train)## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -2.2905 -0.1395 -0.0528 -0.0189 3.3346 ## ## Coefficients:## Estimate Std. Error z value Pr(>|z|) ## (Intercept) -1.101e+01 4.887e-01 -22.52 <2e-16 ***## balance 5.669e-03 2.949e-04 19.22 <2e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## (Dispersion parameter for binomial family taken to be 1)## ## Null deviance: 1723.03 on 6046 degrees of freedom## Residual deviance: 908.69 on 6045 degrees of freedom## AIC: 912.69## ## Number of Fisher Scoring iterations: 8Evaluarea coeficienților
Tabelul de mai jos prezintă estimările coeficienților și informațiile aferente care rezultă din ajustarea unui model de regresie logistică pentru a prezice probabilitatea de neplată = Da folosind soldul. Țineți cont de faptul că estimările coeficienților din regresia logistică caracterizează relația dintre variabila predictor și cea de răspuns pe o scară de cote logaritmice (a se vedea cap. 3 din ISLR1 pentru mai multe detalii). Astfel, vedem că ; acest lucru indică faptul că o creștere a soldului este asociată cu o creștere a probabilității de neplată. Mai exact, o creștere de o unitate a soldului este asociată cu o creștere a șanselor logaritmice de neplată cu 0,0057 unități.
tidy(model1)## term estimate std.error statistic p.value## 1 (Intercept) -11.006277528 0.488739437 -22.51972 2.660162e-112## 2 balance 0.005668817 0.000294946 19.21985 2.525157e-82Potem interpreta în continuare coeficientul de sold ca – pentru fiecare creștere de un dolar a soldului lunar purtat, șansele ca clientul să intre în incapacitate de plată cresc cu un factor de 1.0057.
exp(coef(model1))## (Intercept) balance ## 1.659718e-05 1.005685e+00Multe aspecte ale rezultatului coeficientului sunt similare cu cele discutate în rezultatul regresiei liniare. De exemplu, putem măsura intervalele de încredere și precizia estimărilor coeficienților prin calcularea erorilor standard ale acestora. De exemplu, are o valoare p < 2e-16 care sugerează o relație semnificativă din punct de vedere statistic între soldul purtat și probabilitatea de intrare în incapacitate de plată. Putem, de asemenea, să folosim erorile standard pentru a obține intervale de încredere, așa cum am făcut în tutorialul de regresie liniară:
confint(model1)## 2.5 % 97.5 %## (Intercept) -12.007610373 -10.089360652## balance 0.005111835 0.006269411Facerea de predicții
După ce coeficienții au fost estimați, este o chestiune simplă să calculăm probabilitatea de neplată pentru orice sold dat al cardului de credit. Din punct de vedere matematic, folosind estimările coeficienților din modelul nostru, prezicem că probabilitatea de neplată pentru o persoană cu un sold de 1.000 de dolari este mai mică de 0,5%
Potem prezice probabilitatea de neplată în R folosind funcția predict (asigurați-vă că includeți type = "response"). Aici comparăm probabilitatea de intrare în incapacitate de plată pe baza unor solduri de 1 000 $ și 2 000 $. După cum puteți vedea, pe măsură ce soldul trece de la 1000 $ la 2000 $, probabilitatea de neplată crește semnificativ, de la 0,5% la 58%!
predict(model1, data.frame(balance = c(1000, 2000)), type = "response")## 1 2 ## 0.004785057 0.582089269Se pot folosi și predictori calitativi cu modelul de regresie logistică. Ca exemplu, putem ajusta un model care utilizează variabila student.
model2 <- glm(default ~ student, family = "binomial", data = train)tidy(model2)## term estimate std.error statistic p.value## 1 (Intercept) -3.5534091 0.09336545 -38.05914 0.000000000## 2 studentYes 0.4413379 0.14927208 2.95660 0.003110511Ceficientul asociat cu student = Yes este pozitiv, iar valoarea p asociată este semnificativă din punct de vedere statistic. Acest lucru indică faptul că studenții tind să aibă probabilități de neplată mai mari decât non-tudenții. De fapt, acest model sugerează că un student are aproape de două ori mai multe șanse de a intra în incapacitate de plată decât non-tudenții. Cu toate acestea, în secțiunea următoare vom vedea de ce.
predict(model2, data.frame(student = factor(c("Yes", "No"))), type = "response")## 1 2 ## 0.04261206 0.02783019Regresie logistică multiplă
De asemenea, putem extinde modelul nostru, așa cum se vede în Ecuația 1 astfel încât să putem prezice un răspuns binar folosind predictori multipli unde sunt p predictori:
Să mergem mai departe și să ajustăm un model care prezice probabilitatea de neplată pe baza variabilelor sold, venit (în mii de dolari) și statut de student. Există un rezultat surprinzător aici. Valorile p asociate cu soldul și statutul de student=Da sunt foarte mici, ceea ce indică faptul că fiecare dintre aceste variabile este asociată cu probabilitatea de neplată. Cu toate acestea, coeficientul pentru variabila student este negativ, ceea ce indică faptul că studenții au o probabilitate mai mică de a intra în incapacitate de plată decât non-tudenții. În schimb, coeficientul pentru variabila student în modelul 2, în care am prezis probabilitatea de neplată doar pe baza statutului de student, indică faptul că studenții au o probabilitate mai mare de neplată. Ce se întâmplă?
model3 <- glm(default ~ balance + income + student, family = "binomial", data = train)tidy(model3)## term estimate std.error statistic p.value## 1 (Intercept) -1.090704e+01 6.480739e-01 -16.8299277 1.472817e-63## 2 balance 5.907134e-03 3.102425e-04 19.0403764 7.895817e-81## 3 income -5.012701e-06 1.078617e-05 -0.4647343 6.421217e-01## 4 studentYes -8.094789e-01 3.133150e-01 -2.5835947 9.777661e-03Panelul din dreapta al figurii de mai jos oferă o explicație pentru această discrepanță. Variabilele student și sold sunt corelate. Studenții tind să dețină niveluri mai ridicate de îndatorare, care, la rândul lor, sunt asociate cu o probabilitate mai mare de neplată. Cu alte cuvinte, este mai probabil ca studenții să aibă solduri mari ale cardurilor de credit, care, după cum știm din panoul din stânga al figurii de mai jos, tind să fie asociate cu rate ridicate de neplată. Astfel, chiar dacă un student individual cu un anumit sold al cardului de credit va tinde să aibă o probabilitate mai mică de neplată decât o persoană care nu este studentă și care are același sold al cardului de credit, faptul că studenții, în ansamblu, tind să aibă solduri mai mari ale cardurilor de credit înseamnă că, în general, studenții tind să nu plătească la o rată mai mare decât persoanele care nu sunt studente. Aceasta este o distincție importantă pentru o companie de carduri de credit care încearcă să determine cui ar trebui să ofere credite. Un student este mai riscant decât un nestudent dacă nu sunt disponibile informații despre soldul cardului de credit al studentului. Cu toate acestea, acel student este mai puțin riscant decât un nestudent cu același sold al cardului de credit!
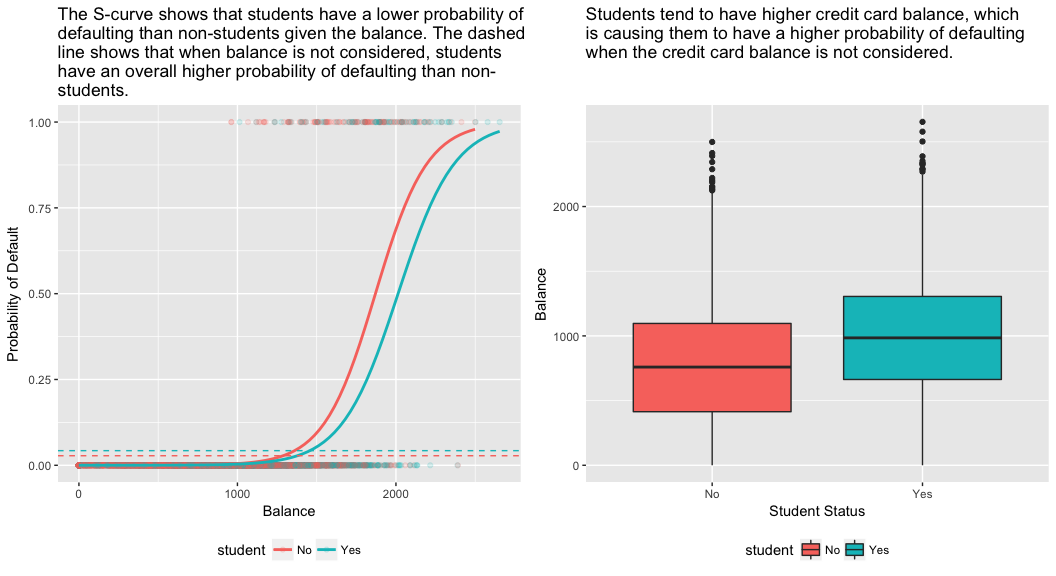
Acest exemplu simplu ilustrează pericolele și subtilitățile asociate cu efectuarea de regresii care implică doar un singur predictor atunci când și alți predictori pot fi relevanți. Rezultatele obținute cu ajutorul unui singur predictor pot fi foarte diferite de cele obținute cu ajutorul mai multor predictori, în special atunci când există corelație între predictori. Acest fenomen este cunoscut sub numele de confuzie.
În cazul variabilelor predictoare multiple, uneori dorim să înțelegem care variabilă este cea mai influentă în predicția variabilei de răspuns (Y). Putem face acest lucru cu varImp din pachetul caret. Aici, vedem că echilibrul este cel mai important cu o marjă mare, în timp ce statutul de student este mai puțin important, urmat de venit (care s-a dovedit a fi oricum nesemnificativ (p = 0,64)).
caret::varImp(model3)## Overall## balance 19.0403764## income 0.4647343## studentYes 2.5835947Ca și înainte, putem face cu ușurință predicții cu acest model. De exemplu, un student cu un sold al cardului de credit de 1 500 de dolari și un venit de 40 000 de dolari are o probabilitate estimată de neîndeplinire a obligațiilor de plată de
Un nestudent cu același sold și același venit are o probabilitate estimată de neîndeplinire a obligațiilor de plată de
new.df <- tibble(balance = 1500, income = 40, student = c("Yes", "No"))predict(model3, new.df, type = "response")## 1 2 ## 0.05437124 0.11440288Așa, vedem că, pentru un sold și un venit date (deși venitul este nesemnificativ), un student are aproximativ jumătate din probabilitatea de neîndeplinire a obligațiilor de plată decât un nestudent.
Evaluarea modelului & Diagnostice
Până acum au fost construite trei modele de regresie logistică și au fost examinați coeficienții. Cu toate acestea, rămân câteva întrebări critice. Sunt modelele bune? Cât de bine se potrivește modelul cu datele? Și cât de precise sunt predicțiile pe un set de date în afara eșantionului?
Buna adecvare a modelului
În tutorialul de regresie liniară am văzut cum diagnosticele F-statistic, și ajustat , și rezidual ne informează despre cât de bine se potrivește modelul la date. Aici, vom examina câteva modalități de evaluare a bonității de potrivire a modelelor noastre logit.
Testul raportului de verosimilitate
În primul rând, putem utiliza un test al raportului de verosimilitate pentru a evalua dacă modelele noastre îmbunătățesc potrivirea. Adăugarea de variabile predictive la un model va îmbunătăți aproape întotdeauna ajustarea modelului (adică va crește probabilitatea logaritmică și va reduce devianța modelului în comparație cu devianța nulă), dar este necesar să se testeze dacă diferența observată în ajustarea modelului este semnificativă din punct de vedere statistic. Putem utiliza anova pentru a efectua acest test. Rezultatele indică faptul că, în comparație cu model1, model3 reduce devianța reziduală cu peste 13 (rețineți, un obiectiv al regresiei logistice este acela de a găsi un model care minimizează devianța reziduală). Mai important, această îmbunătățire este semnificativă din punct de vedere statistic la p = 0,001. Acest lucru sugerează că model3 oferă într-adevăr o potrivire îmbunătățită a modelului.
anova(model1, model3, test = "Chisq")## Analysis of Deviance Table## ## Model 1: default ~ balance## Model 2: default ~ balance + income + student## Resid. Df Resid. Dev Df Deviance Pr(>Chi) ## 1 6045 908.69 ## 2 6043 895.02 2 13.668 0.001076 **## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Pseudo
În comparație cu regresia liniară cu estimare prin metoda celor mai mici pătrate ordinare, nu există o statistică care să explice proporția de varianță din variabila dependentă care este explicată de predictori. Cu toate acestea, există o serie de pseudo-metrici care ar putea fi utile. Cea mai notabilă este McFadden’s , care este definită ca
unde este valoarea logaritmică a verosimilitudinii pentru modelul ajustat și este logaritmul verosimilitudinii pentru modelul nul cu doar o intercepție ca predictor. Măsura variază de la 0 la puțin sub 1, valorile mai apropiate de zero indicând că modelul nu are putere predictivă. Cu toate acestea, spre deosebire de regresia liniară, modelele rareori ating o valoare ridicată a lui McFadden . De fapt, în cuvintele lui McFadden, modelele cu un pseudo McFadden reprezintă o potrivire foarte bună. Putem evalua valorile pseudo McFadden pentru modelele noastre cu:
list(model1 = pscl::pR2(model1), model2 = pscl::pR2(model2), model3 = pscl::pR2(model3))## $model1## McFadden ## 0.4726215 ## ## $model2## McFadden ## 0.004898314 ## ## $model3## McFadden ## 0.4805543Vezi că modelul 2 are o valoare foarte scăzută care corobrează potrivirea sa slabă. Cu toate acestea, modelele 1 și 3 au valori mult mai mari, sugerând că explică o cantitate destul de mare de variație în datele implicite. Mai mult, vedem că modelul 3 îmbunătățește doar foarte puțin.
Evaluare reziduală
Rețineți că regresia logistică nu presupune că reziduurile sunt distribuite în mod normal și nici că varianța este constantă. Cu toate acestea, reziduul devianței este util pentru a determina dacă punctele individuale nu sunt bine adaptate de către model. Aici putem ajusta reziduurile devianței standardizate pentru a vedea câte dintre ele depășesc 3 deviații standard. Mai întâi extragem câteva fragmente utile din rezultatele modelului cu augment și apoi procedăm la trasare.
model1_data <- augment(model1) %>% mutate(index = 1:n())ggplot(model1_data, aes(index, .std.resid, color = default)) + geom_point(alpha = .5) + geom_ref_line(h = 3)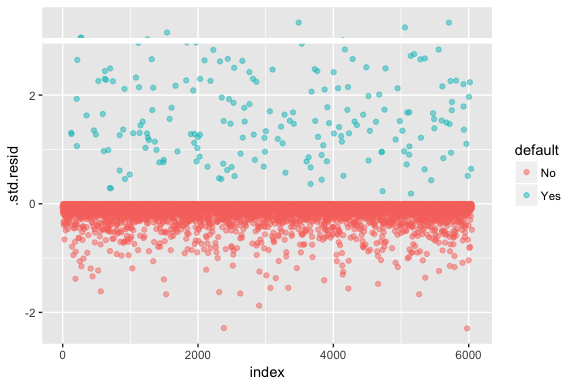
Aceste reziduuri standardizate care depășesc 3 reprezintă posibile valori aberante și pot merita o atenție mai atentă. Putem filtra pentru aceste reziduuri pentru a obține o privire mai atentă. Vedem că toate aceste observații reprezintă clienți care au intrat în incapacitate de plată cu bugete mult mai mici decât cei care intră în incapacitate de plată în mod normal.
model1_data %>% filter(abs(.std.resid) > 3)## default balance .fitted .se.fit .resid .hat .sigma .cooksd .std.resid index## 1 Yes 1118.7010 -4.664566 0.1752745 3.057432 0.0002841609 0.3857438 0.01508609 3.057867 271## 2 Yes 1119.0972 -4.662320 0.1751742 3.056704 0.0002844621 0.3857448 0.01506820 3.057139 272## 3 Yes 1135.0473 -4.571902 0.1711544 3.027272 0.0002967274 0.3857832 0.01435943 3.027721 1253## 4 Yes 1066.8841 -4.958307 0.1885550 3.151288 0.0002463229 0.3856189 0.01754100 3.151676 1542## 5 Yes 961.4889 -5.555773 0.2163846 3.334556 0.0001796165 0.3853639 0.02324417 3.334855 3488## 6 Yes 1143.6805 -4.522962 0.1689933 3.011233 0.0003034789 0.3858039 0.01398491 3.011690 4142## 7 Yes 1013.2169 -5.262537 0.2026075 3.245830 0.0002105772 0.3854892 0.02032614 3.246172 5058## 8 Yes 961.7327 -5.554391 0.2163192 3.334143 0.0001797543 0.3853645 0.02322988 3.334443 5709În mod similar cu regresia liniară, putem, de asemenea, să identificăm observațiile influente cu ajutorul valorilor distanței lui Cook. Aici identificăm primele 5 cele mai mari valori.
plot(model1, which = 4, id.n = 5)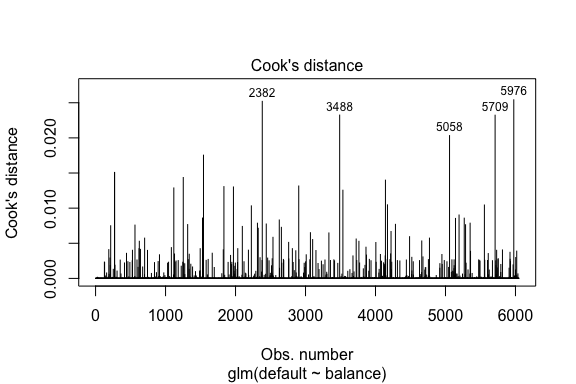
Și le putem investiga și pe acestea în continuare. Aici vedem că primele cinci puncte influente includ:
- cei clienți care au intrat în incapacitate de plată cu solduri foarte mici și
- doi clienți care nu au intrat în incapacitate de plată, dar care aveau solduri de peste 2.000 de dolari
Aceasta înseamnă că, dacă am elimina aceste observații (nerecomandat), forma, locația și intervalul de încredere al curbei noastre în S de regresie logistică s-ar schimba probabil.
model1_data %>% top_n(5, .cooksd)## default balance .fitted .se.fit .resid .hat .sigma .cooksd .std.resid index## 1 No 2388.1740 2.531843 0.2413764 -2.284011 0.0039757771 0.3866249 0.02520100 -2.288565 2382## 2 Yes 961.4889 -5.555773 0.2163846 3.334556 0.0001796165 0.3853639 0.02324417 3.334855 3488## 3 Yes 1013.2169 -5.262537 0.2026075 3.245830 0.0002105772 0.3854892 0.02032614 3.246172 5058## 4 Yes 961.7327 -5.554391 0.2163192 3.334143 0.0001797543 0.3853645 0.02322988 3.334443 5709## 5 No 2391.0077 2.547907 0.2421522 -2.290521 0.0039468742 0.3866185 0.02542145 -2.295054 5976Validarea valorilor prezise
Taxa de clasificare
Când se dezvoltă modele pentru predicție, cea mai critică măsurătoare se referă la cât de bine se descurcă modelul în prezicerea variabilei țintă pe observațiile din afara eșantionului. În primul rând, trebuie să folosim modelele estimate pentru a prezice valori pe setul nostru de date de instruire (train). Atunci când folosiți predict asigurați-vă că includeți type = response astfel încât predicția să returneze probabilitatea de neplată.
test.predicted.m1 <- predict(model1, newdata = test, type = "response")test.predicted.m2 <- predict(model2, newdata = test, type = "response")test.predicted.m3 <- predict(model3, newdata = test, type = "response")Acum putem compara variabila țintă prezisă față de valorile observate pentru fiecare model și să vedem care dintre ele se comportă cel mai bine. Putem începe prin a utiliza matricea de confuzie, care este un tabel care descrie performanța de clasificare pentru fiecare model pe datele de testare. Fiecare cadran al tabelului are o semnificație importantă. În acest caz, „Nu” și „Da” din rânduri reprezintă dacă clienții au intrat sau nu în incapacitate de plată. „FALSE” și „TRUE” din coloane reprezintă dacă am prezis că clienții vor intra sau nu în incapacitate de plată.
- adevărate pozitive (cadranul din dreapta jos): acestea sunt cazuri în care am prezis că clientul va intra în incapacitate de plată și a intrat în incapacitate de plată.
- adevărate negative (cadranul din stânga sus): Am prezis că nu a existat nicio incapacitate de plată, iar clientul nu a intrat în incapacitate de plată.
- false pozitive (Cadranul de sus-dreapta): Am prezis da, dar clientul nu a intrat de fapt în incapacitate de plată. (Cunoscută și sub numele de „eroare de tip I.”)
- false negative (Cadranul din stânga jos): Am prezis că nu, dar au intrat în incapacitate de plată. (Cunoscută și sub numele de „eroare de tip II”)
Rezultatele arată că model1 și model3 sunt foarte asemănătoare. 96% dintre observațiile prezise sunt adevărate negative și aproximativ 1% sunt adevărate pozitive. Ambele modele au o eroare de tip II mai mică de 3%, în care modelul prezice că clientul nu va intra în incapacitate de plată, dar în realitate a intrat în incapacitate de plată. Ambele modele au o eroare de tip I mai mică de 1% în cazul în care modelul prezice că clientul nu va plăti, dar nu a făcut-o niciodată. model2 rezultatele sunt remarcabil de diferite; acest model prezice cu exactitate persoanele care nu se află în incapacitate de plată (un rezultat al faptului că 97% din date sunt persoane care nu se află în incapacitate de plată), dar niciodată nu prezice de fapt acei clienți care se află în incapacitate de plată!
list( model1 = table(test$default, test.predicted.m1 > 0.5) %>% prop.table() %>% round(3), model2 = table(test$default, test.predicted.m2 > 0.5) %>% prop.table() %>% round(3), model3 = table(test$default, test.predicted.m3 > 0.5) %>% prop.table() %>% round(3))## $model1## ## FALSE TRUE## No 0.962 0.003## Yes 0.025 0.010## ## $model2## ## FALSE## No 0.965## Yes 0.035## ## $model3## ## FALSE TRUE## No 0.963 0.003## Yes 0.026 0.009De asemenea, dorim să înțelegem ratele de neclasificare (aka eroare) (sau am putea inversa acest lucru cu ratele de acuratețe). Nu observăm o îmbunătățire prea mare între modelele 1 și 3 și, deși modelul 2 are o rată de eroare scăzută, nu uitați că acesta nu prezice niciodată cu exactitate clienții care, de fapt, intră în incapacitate de plată.
test %>% mutate(m1.pred = ifelse(test.predicted.m1 > 0.5, "Yes", "No"), m2.pred = ifelse(test.predicted.m2 > 0.5, "Yes", "No"), m3.pred = ifelse(test.predicted.m3 > 0.5, "Yes", "No")) %>% summarise(m1.error = mean(default != m1.pred), m2.error = mean(default != m2.pred), m3.error = mean(default != m3.pred))## # A tibble: 1 × 3## m1.error m2.error m3.error## <dbl> <dbl> <dbl>## 1 0.02782697 0.03491019 0.02807994Potem obține câteva informații suplimentare dacă analizăm valorile brute (nu procentele) din matricea noastră de confuzie. Să ne uităm la modelul 1 pentru a ilustra. Vedem că există un total de clienți care au intrat în incapacitate de plată. Din totalul neplăților, nu au fost prezise. Alternativ, am putea spune că doar o parte din cazurile de neplată au fost prezise – acest lucru este cunoscut sub numele de precizie (cunoscută și sub numele de sensibilitate) a modelului nostru. Deci, în timp ce rata globală de eroare este scăzută, rata de precizie este, de asemenea, scăzută, ceea ce nu este bine!
table(test$default, test.predicted.m1 > 0.5)## ## FALSE TRUE## No 3803 12## Yes 98 40Cu modelele de clasificare veți auzi aici și termenii de sensibilitate și specificitate atunci când caracterizați performanța modelului. După cum s-a menționat mai sus, sensibilitatea este sinonimă cu precizia. Cu toate acestea, specificitatea este procentul de persoane care nu se află în situație de neîndeplinire a obligațiilor de plată și care sunt identificate corect, aici (precizia este determinată în mare măsură de faptul că 97 % din observațiile din datele noastre sunt persoane care nu se află în situație de neîndeplinire a obligațiilor de plată). Importanța dintre sensibilitate și specificitate depinde de context. În acest caz, este probabil ca o companie de carduri de credit să fie mai preocupată de sensibilitate, deoarece dorește să își reducă riscul. Prin urmare, este posibil ca acestea să fie mai preocupate de reglarea unui model astfel încât sensibilitatea/precizia lor să fie îmbunătățită.
Caracteristica de funcționare a recepției (ROC) este o măsură vizuală a performanței clasificatorului. Utilizând proporția de puncte de date pozitive care sunt considerate corect ca fiind pozitive și proporția de puncte de date negative care sunt considerate eronat ca fiind pozitive, se generează un grafic care arată compromisul dintre rata la care puteți prezice corect ceva și rata de prezicere incorectă a ceva. În cele din urmă, suntem preocupați de aria de sub curba ROC, sau AUC. Această măsură variază de la 0,50 la 1,00, iar valorile de peste 0,80 indică faptul că modelul face o treabă bună în ceea ce privește discriminarea între cele două categorii care cuprind variabila noastră țintă. Putem compara ROC și AUC pentru modelele 1 și 2, care arată o diferență puternică în ceea ce privește performanța. Ne dorim cu siguranță ca graficele noastre ROC să semene mai degrabă cu cele ale modelului 1 (stânga) decât cu cele ale modelului 2 (dreapta)!
library(ROCR)par(mfrow=c(1, 2))prediction(test.predicted.m1, test$default) %>% performance(measure = "tpr", x.measure = "fpr") %>% plot()prediction(test.predicted.m2, test$default) %>% performance(measure = "tpr", x.measure = "fpr") %>% plot()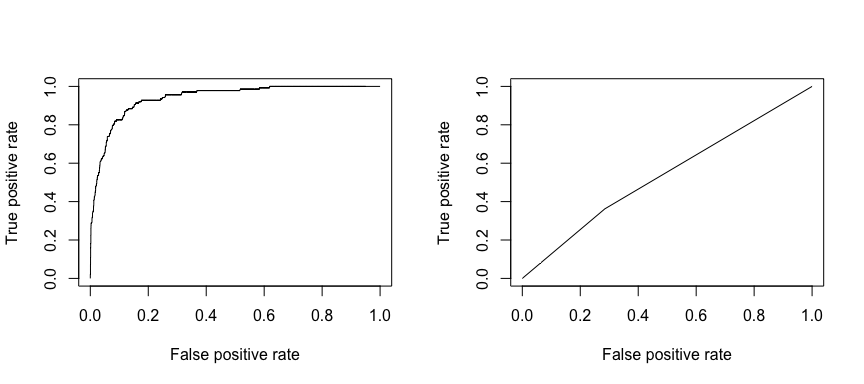
Și pentru a calcula numeric AUC putem folosi următoarele. Nu uitați, AUC va fi cuprinsă între 0,50 – 1,00. Astfel, modelul 2 este un model de clasificare foarte slab, în timp ce modelul 1 este un model de clasificare foarte bun.
# model 1 AUCprediction(test.predicted.m1, test$default) %>% performance(measure = "auc") %>% [email protected]## ]## 0.939932# model 2 AUCprediction(test.predicted.m2, test$default) %>% performance(measure = "auc") %>% [email protected]## ]## 0.5386955Putem continua să ne „acordăm” modelele pentru a îmbunătăți aceste rate de clasificare. Dacă vă puteți îmbunătăți curbele AUC și ROC (ceea ce înseamnă că îmbunătățiți ratele de acuratețe a clasificării), creați un „lift”, ceea ce înseamnă că ridicați acuratețea clasificării.
Resurse suplimentare
Acesta vă va ajuta să vă familiarizați cu regresia logistică. Rețineți că puteți aprofunda mult mai mult, așa că următoarele resurse vă vor ajuta să aflați mai multe:
- An Introduction to Statistical Learning
- Applied Predictive Modeling
- Elements of Statistical Learning
-
Acest tutorial a fost construit ca un supliment la capitolul 4, secțiunea 3 din An Introduction to Statistical Learning 2
.