Timpul de înjumătățire

Figura 1. O diagramă care arată dezintegrarea unui nucleu radioactiv în timp. Timpul necesar pentru ca masa sau activitatea sursei (numărul de evenimente de dezintegrare pe secundă) să scadă până la pragul de 50% reprezintă timpul de înjumătățire. Timpul de înjumătățire din această imagine este de 1 an.

Jumătatea de viață este timpul necesar pentru ca jumătate din valoarea inițială a unei anumite cantități dintr-un element radioactiv să se dezintegreze. În plus, o perioadă de înjumătățire este timpul necesar pentru ca activitatea unei surse să scadă la jumătate din valoarea sa inițială. A doua lege a termodinamicii, în special afirmația de dezordine, poate fi utilizată pentru a înțelege de ce are loc dezintegrarea radioactivă. Această afirmație spune că entropia unui sistem închis nu poate scădea niciodată, ceea ce înseamnă că lucrurile trebuie să continue să cadă în dezordine, nu în ordine. Acest proces este cunoscut sub numele de „descompunere”, iar cea de-a doua lege ajută la clarificarea motivului pentru care materia se descompune într-o stare din ce în ce mai puțin organizată în timp acest . O parte a acestui proces include anumite tipuri de atomi care se descompun în tipuri noi și diferite de atomi la o anumită rată măsurabilă cunoscută sub numele de dezintegrare radioactivă.

Toate materialele radioactive au nuclee instabile în interiorul lor. În plus, există, de asemenea, unele nuclee în cadrul substanței care se află deja în starea lor stabilă, dar proporția de nuclee stabile față de cele instabile într-un eșantion poate varia. Nucleii stabili din eșantion sunt neschimbate (și într-o stare energetică stabilă), dar nucleele instabile vor suferi un fel de dezintegrare nucleară în timp pentru a deveni stabile. Acest lucru are ca rezultat o emisie de o anumită formă de radiație. Deoarece timpul de înjumătățire este o măsură de timp, timpul de înjumătățire este o valoare care determină cât timp va dura această reducere la o stare energetică mai stabilă.

Diferite substanțe experimentează o pierdere a radioactivității lor mai repede decât altele. Unele elemente radioactive pot avea jumătate din nucleele lor instabile care se dezintegrează în mai puțin de o secundă. De exemplu, kripton-101 are un timp de înjumătățire de aproximativ o zecime de milionime de secundă. În schimb, unele elemente au perioade de înjumătățire extraordinar de lungi și au nevoie de miliarde de ani pentru a se dezintegra. Uraniul-238 are un timp de înjumătățire de 4,51 miliarde de ani. Acest lucru înseamnă că ar fi nevoie de miliarde de ani pentru ca uraniul-238 să se dezintegreze într-un raport de jumătate de uraniu-238 și jumătate de toriu-234. Uraniul-235 (un alt izotop natural al uraniului) are un timp de înjumătățire mai scurt decât uraniul-238, adică doar ~700 de milioane de ani.

Ecuația

Există o ecuație care este folosită frecvent pentru a determina cât de mult a rămas dintr-o anumită substanță radioactivă după ce a trecut un anumit timp. Aceasta se determină pe baza unor proprietăți precum perioada de înjumătățire a substanței și a cantității de substanță care a existat inițial. Ecuația utilizată este:

în care:

• este cantitatea de substanță după ce a trecut timpul
• este cantitatea inițială de substanță
• este cantitatea de timp care a trecut
• este timpul de înjumătățire a substanței

În plus, o ecuație similară poate fi utilizată pentru a arăta cum scade activitatea substanței în timp. Atunci când aceasta este exprimată, ecuația ia forma:

unde:

• este activitatea substanței după trecerea timpului
• este activitatea inițială a substanței
• este timpul care a trecut
• este timpul care a trecut
• este timpul de înjumătățire al substanței

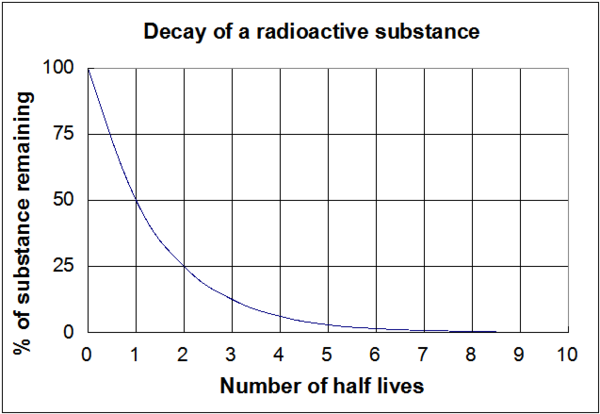
Graficul prezentat în figura 1 este o reprezentare vizuală a acestor ecuații de mai sus. Este important de reținut că, indiferent de lungimea reală a timpului de înjumătățire (fie că este de milioane de ani sau de câteva nanosecunde), forma graficului va fi aceeași.

Cunoașterea timpilor de înjumătățire face parte din modul în care geologii datează rocile cu ajutorul datării radioizotopice.

.