Aufbyggnadsprincipen
För att bestämma elektronkonfigurationen för en viss atom kan vi ”bygga upp” strukturerna i atomnummerordning. Vi börjar med väte och fortsätter genom perioderna i det periodiska systemet och lägger till en proton i taget till kärnan och en elektron till det rätta underskalet tills vi har beskrivit elektronkonfigurationen för alla grundämnen. Detta förfarande kallas Aufbau-principen, från det tyska ordet Aufbau (”bygga upp”). Varje tillagd elektron upptar det underskal med lägsta tillgängliga energi (i den ordning som visas i figur \(\PageIndex{3}\)), med förbehåll för de begränsningar som de tillåtna kvanttalen enligt Paulis uteslutningsprincip medför. Elektroner går in i delskal med högre energi först efter att delskal med lägre energi har fyllts upp till kapacitet. Figur \(\PageIndex{3}\) illustrerar det traditionella sättet att komma ihåg fyllnadsordningen för atomorbitaler.
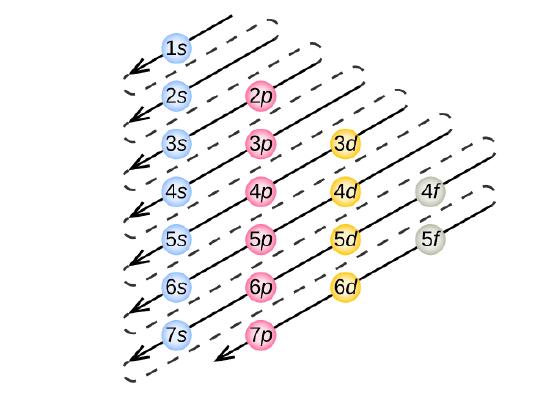
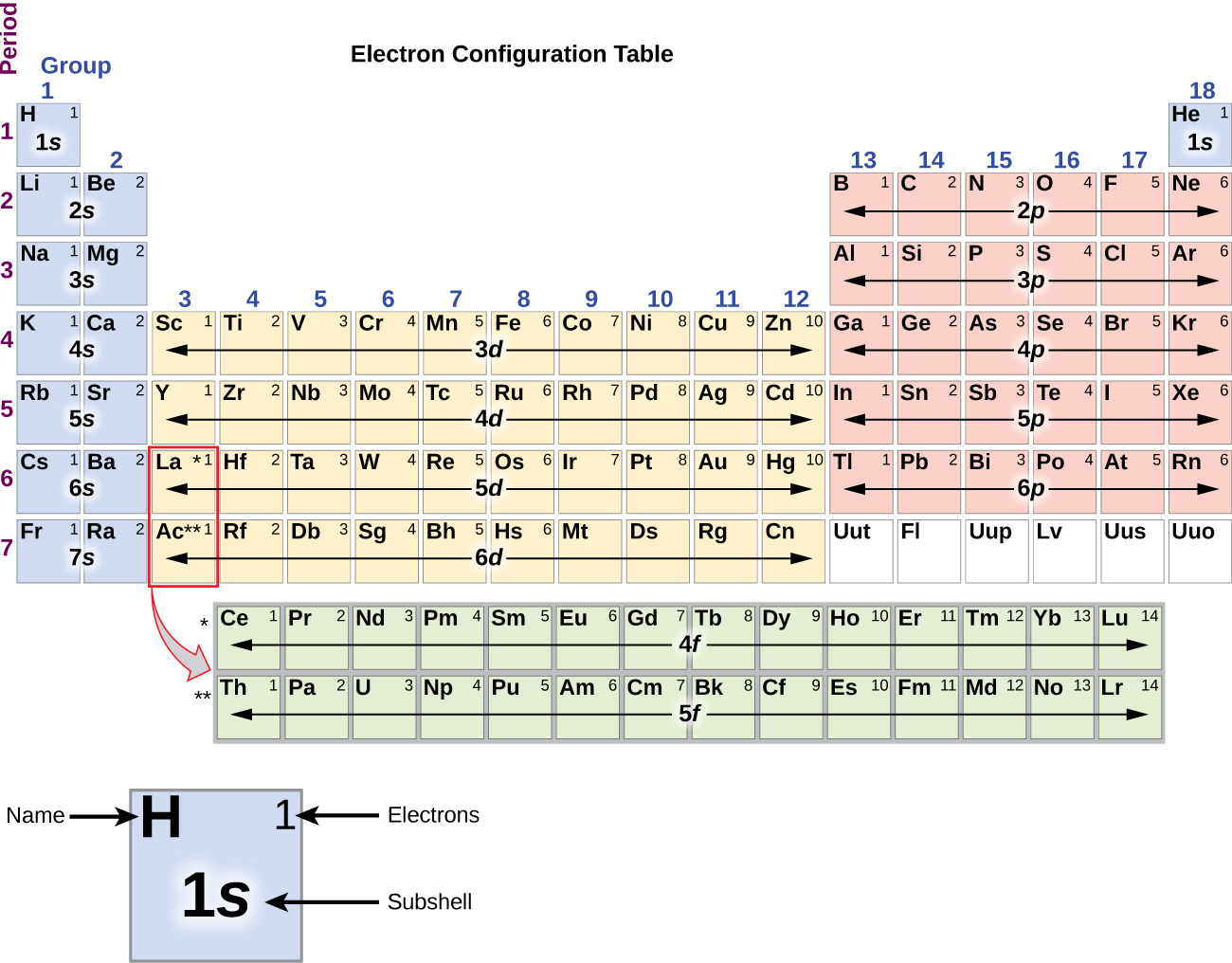
Då det periodiska systemets arrangemang är baserat på elektronkonfigurationerna ger figur \(\PageIndex{4}\) en alternativ metod för att bestämma elektronkonfigurationen. Fyllnadsordningen börjar helt enkelt vid väte och inkluderar varje underskal när du fortsätter i ökande Z-ordning. Till exempel, efter att ha fyllt 3p-blocket upp till Ar, ser vi att orbitalet kommer att vara 4s (K, Ca), följt av 3d-orbitalerna.
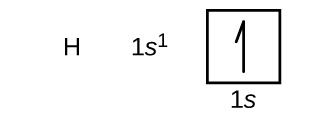
Vi kommer nu att konstruera elektronkonfigurationen i grundtillståndet och orbitaldiagrammet för ett urval av atomer i den första och andra perioden i det periodiska systemet. Orbitaldiagram är en bildlig representation av elektronkonfigurationen, som visar de enskilda orbitalerna och elektronernas parningsarrangemang. Vi börjar med en enda väteatom (atomnummer 1), som består av en proton och en elektron. Om vi hänvisar till antingen figur \(\PageIndex{3}\) eller \(\PageIndex{4}\), kan vi förvänta oss att elektronerna befinner sig i 1s orbital. Enligt konvention fylls värdet \(m_s=+\dfrac{1}{2}\) vanligtvis först. Elektronkonfigurationen och bandiagrammet är:
Efter väte kommer ädelgasen helium, som har atomnumret 2. Heliumatomen innehåller två protoner och två elektroner. Den första elektronen har samma fyra kvantnummer som väteatomens elektron (n = 1, l = 0, ml = 0, \(m_s=+\dfrac{1}{2}\)). Den andra elektronen går också in i 1s-blocket och fyller det. Den andra elektronen har samma kvantantal n, l och ml, men måste ha motsatt spinkvantantal, \(m_s=-\dfrac{1}{2}\). Detta stämmer överens med Paulis uteslutningsprincip: Inga två elektroner i samma atom kan ha samma uppsättning av fyra kvantnummer. För orbitaldiagram innebär detta att två pilar går in i varje ruta (vilket representerar två elektroner i varje orbital) och pilarna måste peka i motsatt riktning (vilket representerar parade spinn). Elektronkonfigurationen och orbitaldiagrammet för helium är:
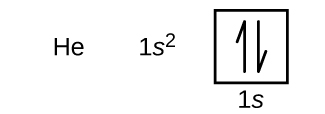
Heliumatomens n = 1-hölje är helt fyllt.
Nästa atom är alkalimetallen litium med atomnumret 3. De två första elektronerna i litium fyller 1s-bitalet och har samma uppsättningar av fyra kvanttal som de två elektronerna i helium. Den återstående elektronen måste ockupera orbitalet med näst lägst energi, 2s orbitalet (figur \(\PageIndex{3}\) eller \(\(\PageIndex{4}\))). Elektronkonfigurationen och orbitaldiagrammet för litium är således:
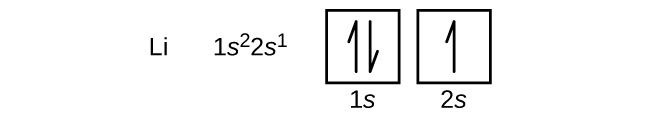
En atom av den alkaliska jordartsmetallen beryllium, med atomnumret 4, innehåller fyra protoner i kärnan och fyra elektroner som omger kärnan. Den fjärde elektronen fyller det återstående utrymmet i 2s-bitalet.
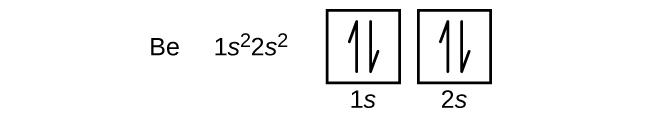
En atom av bor (atomnummer 5) innehåller fem elektroner. N = 1-höljet är fyllt med två elektroner och tre elektroner kommer att ockupera n = 2-höljet. Eftersom varje s-underskal endast kan innehålla två elektroner måste den femte elektronen ockupera nästa energinivå, vilket blir en 2p-orbital. Det finns tre degenererade 2p-orbitaler (ml = -1, 0, +1) och elektronen kan ockupera vilken som helst av dessa p-orbitaler. När vi ritar orbitaldiagram inkluderar vi tomma rutor för att avbilda eventuella tomma orbitaler i samma subskal som vi fyller.

Kol (atomnummer 6) har sex elektroner. Fyra av dem fyller 1s och 2s orbitaler. De återstående två elektronerna upptar 2p-subskalet. Vi har nu ett val mellan att fylla en av 2p-orbitalerna och para ihop elektronerna eller att lämna elektronerna oparade i två olika, men degenererade, p-orbitaler. Orbitalerna fylls på det sätt som beskrivs av Hunds regel: den lägsta energikonfigurationen för en atom med elektroner inom en uppsättning degenererade orbitaler är den som har det högsta antalet oparade elektroner. De två elektronerna i kolets 2p-orbitaler har således identiska n, l och ms kvantnummer och skiljer sig åt i ml-kvantnumret (i enlighet med Paulis uteslutningsprincip). Elektronkonfigurationen och orbitaldiagrammet för kol är:

Väte (atomnummer 7) fyller 1s och 2s underskal och har en elektron i var och en av de tre 2p-orbitalerna, i enlighet med Hunds regel. Dessa tre elektroner har oparade spinn. Syre (atomnummer 8) har ett elektronpar i någon av 2p-orbitalerna (elektronerna har motsatt spinn) och en enkel elektron i var och en av de andra två. Fluor (atomnummer 9) har endast en 2p-orbital som innehåller en oparad elektron. Alla elektroner i ädelgasen neon (atomnummer 10) är parade, och alla orbitaler i n = 1 och n = 2-höljen är fyllda. Elektronkonfigurationerna och orbitaldiagrammen för dessa fyra grundämnen är:
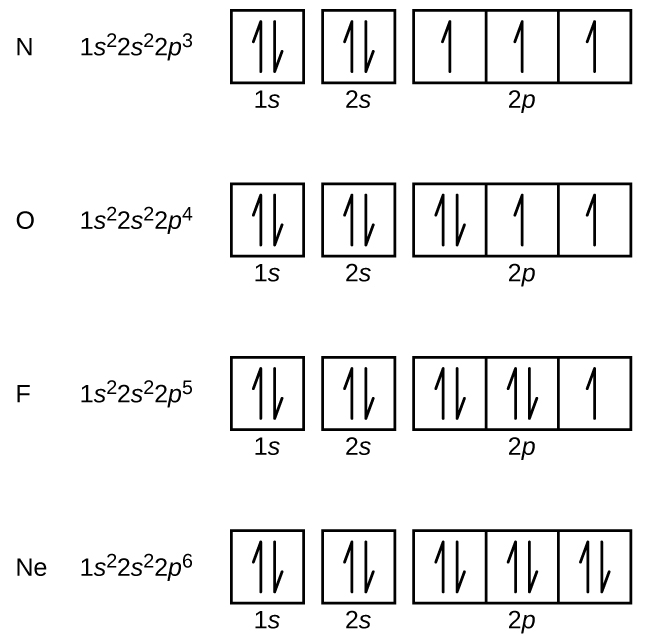
Alkalimetallen natrium (atomnummer 11) har en elektron mer än neonatomen. Denna elektron måste gå in i det lägsta tillgängliga subskalet med lägsta energi, 3s orbitalet, vilket ger en 1s22s22p63s1 konfiguration. De elektroner som upptar de yttersta skalorbitalerna (högsta värdet på n) kallas valenselektroner, och de som upptar de inre skalorbitalerna kallas kärnelektroner (figur \PageIndex5\PageIndex5). Eftersom kärnelektronernas skal motsvarar ädelgasernas elektronkonfigurationer kan vi förkorta elektronkonfigurationerna genom att skriva den ädelgas som matchar kärnelektronkonfigurationen tillsammans med valenceelektronerna i ett komprimerat format. För vårt natriumexempel representerar symbolen kärnelektronerna (1s22s22p6) och vår förkortade eller kondenserade konfiguration är 3s1.

På samma sätt kan litiums förkortade konfiguration representeras som 2s1, där den representerar heliumatomens konfiguration, som är identisk med den för litiums fyllda inre skal. Genom att skriva konfigurationerna på detta sätt betonas likheten mellan litiums och natriums konfigurationer. Båda atomerna, som tillhör alkalimetallfamiljen, har endast en elektron i ett valenssubskal utanför en fylld uppsättning inre skal.
\}\\,2s^1\\\\ \ce{Na:}\,3s^1\]
Den alkaliska jordartsmetallen magnesium (atomnummer 12), med sina 12 elektroner i en 3s2-konfiguration, är analog med sin familjemedlem beryllium, 2s2. Båda atomerna har ett fyllt s-subskal utanför sina fyllda inre skal. Aluminium (atomnummer 13), med 13 elektroner och elektronkonfigurationen 3s23p1, är analogt med familjemedlemmen bor, 2s22p1.
Elektronkonfigurationerna hos kisel (14 elektroner), fosfor (15 elektroner), svavel (16 elektroner), klor (17 elektroner) och argon (18 elektroner) är analoga i elektronkonfigurationerna i sina yttre skal till sina motsvarande familjemedlemmar kol, kväve, syre, fluor respektive neon, med undantag för att det huvudsakliga kvantantalet i det yttre skalet hos de tyngre grundämnena har ökat med en till n = 3. Figur \(\PageIndex{6}\) visar elektronkonfigurationen med lägsta energi, eller grundtillstånd, för dessa grundämnen samt för atomer av vart och ett av de kända grundämnena.
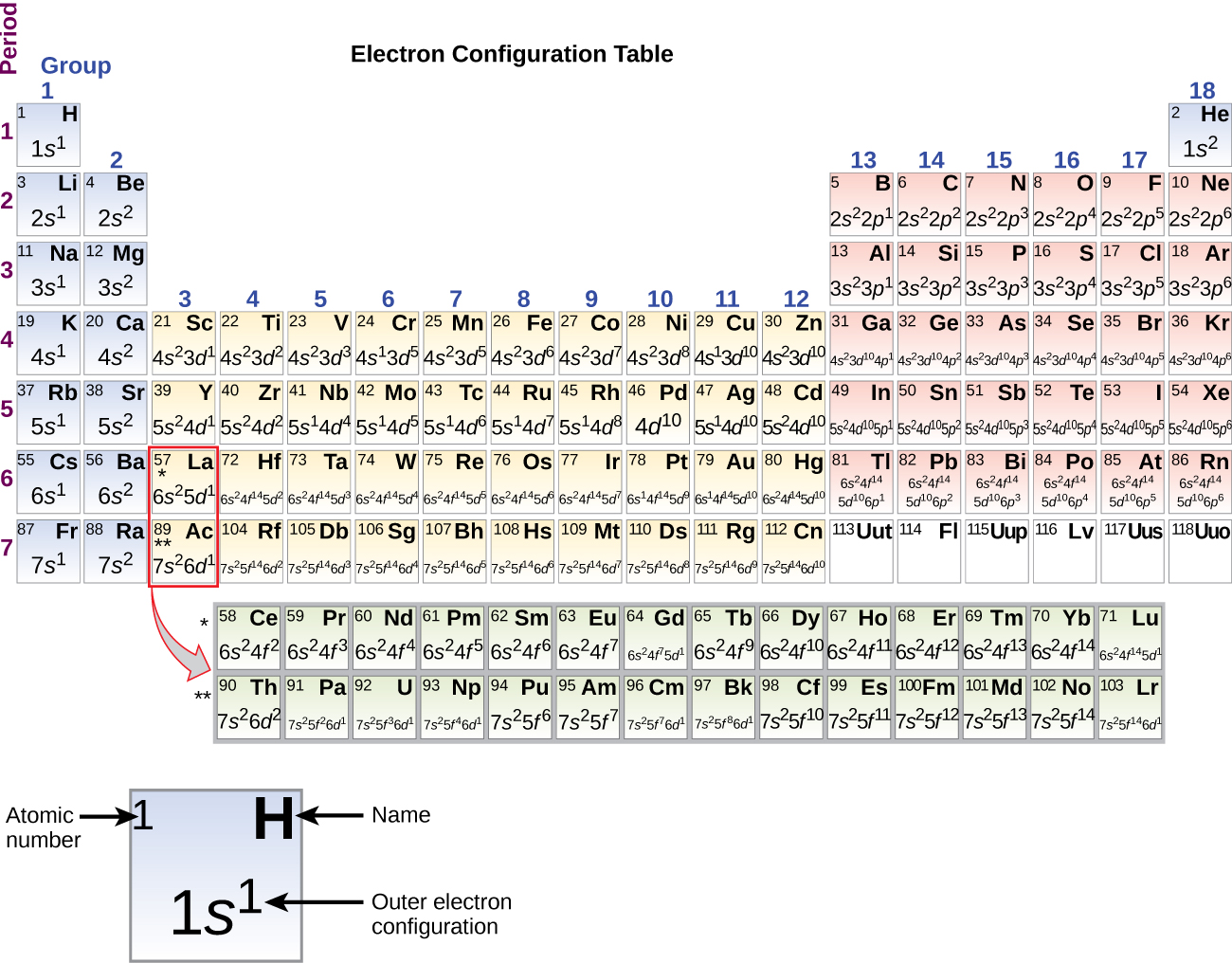
När vi kommer till nästa grundämne i det periodiska systemet, alkalimetallen kalium (atomnummer 19), kan vi förvänta oss att vi skulle börja lägga till elektroner till 3d-underskalet. Alla tillgängliga kemiska och fysikaliska bevis tyder dock på att kalium är som litium och natrium, och att nästa elektron inte läggs till på 3d-nivån utan i stället läggs till på 4snivån (figur \(\PageIndex{3}\) eller \(\(\PageIndex{4}\)). Som tidigare diskuterats är 3d-orbitalet utan radiella noder högre i energi eftersom det är mindre genomträngande och mer avskärmat från kärnan än 4s, som har tre radiella noder. Kalium har således elektronkonfigurationen 4s1. Kalium motsvarar därför Li och Na i sin valensskalkonfiguration. Nästa elektron läggs till för att komplettera 4s-subskalet och kalcium har elektronkonfigurationen 4s2. Detta ger kalcium en elektronkonfiguration i det yttre skalet som motsvarar den för beryllium och magnesium.
Med övergångsmetallen skandium (atomnummer 21) som utgångspunkt läggs ytterligare elektroner successivt till 3d-underskalet. Detta underskal fylls till sin kapacitet med 10 elektroner (kom ihåg att för l = 2 finns det 2l + 1 = 5 värden på ml, vilket innebär att det finns fem d-orbitaler som har en sammanlagd kapacitet på 10 elektroner). Därefter fylls 4p-underskalet. Observera att för tre serier av grundämnen, scandium (Sc) genom koppar (Cu), yttrium (Y) genom silver (Ag) och lutetium (Lu) genom guld (Au), läggs sammanlagt 10 d-elektroner successivt till (n – 1)-skalet bredvid n-skalet för att föra detta (n – 1)-skal från 8 till 18 elektroner. För två serier, lantan (La) genom lutetium (Lu) och aktinium (Ac) genom lawrencium (Lr), läggs 14 f-elektroner (l = 3, 2l + 1 = 7 ml-värden; alltså sju orbitaler med en sammanlagd kapacitet på 14 elektroner) successivt till (n – 2)-höljet för att föra detta hölje från 18 elektroner till totalt 32 elektroner.
Exempel \(\PageIndex{1}\): Kvantumtal och elektronkonfigurationer
Vad är elektronkonfigurationen och orbitaldiagrammet för en fosforatom? Vilka är de fyra kvantnumren för den sista elektronen som lagts till?
Lösning
Atomnumret för fosfor är 15. En fosforatom innehåller således 15 elektroner. Energinivåernas fyllnadsordning är 1s, 2s, 2p, 3s, 3p, 4s, … . Fosforatomens 15 elektroner kommer att fyllas upp till 3p-orbitalet, som kommer att innehålla tre elektroner:
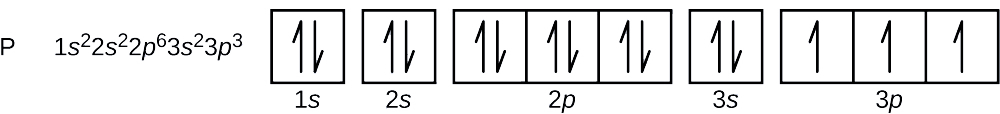
Den sista elektron som läggs till är en 3p-elektron. Därför är n = 3 och, för en p-typ orbital, l = 1. ml-värdet kan vara -1, 0 eller +1. De tre p-orbitalerna är degenererade, så något av dessa ml-värden är korrekt. För oparade elektroner tilldelar konventionen värdet \(+\dfrac{1}{2}\) för spinkvantumtalet; alltså \(m_s=+\dfrac{1}{2}\).
Övningsuppgift \(\PageIndex{1}\)
Identifiera atomerna utifrån de givna elektronkonfigurationerna:
- 4s23d5
- 5s24d105p6
Svar a
Mn
Svar b
Xe
Det periodiska systemet kan vara ett kraftfullt verktyg när det gäller att förutsäga ett grundämnes elektronkonfiguration. Vi finner dock undantag från ordningen för fyllning av orbitaler som visas i figur \(\PageIndex{3}\) eller \(\(\PageIndex{4}\). Till exempel är elektronkonfigurationerna hos övergångsmetallerna krom (Cr; atomnummer 24) och koppar (Cu; atomnummer 29), bland andra, inte de som vi skulle förvänta oss. I allmänhet involverar sådana undantag underskal med mycket likartad energi, och små effekter kan leda till förändringar i fyllnadsordningen.
I fallet med Cr och Cu finner vi att halvt fyllda och helt fyllda underskal tydligen representerar förhållanden med föredragen stabilitet. Denna stabilitet är sådan att en elektron flyttar från 4s till 3d-orbitalet för att få den extra stabiliteten hos ett halvfyllt 3d-subskal (i Cr) eller ett fyllt 3d-subskal (i Cu). Andra undantag förekommer också. Niob (Nb, atomnummer 41) förutspås till exempel ha elektronkonfigurationen 5s24d3. Experimentellt observerar vi att dess elektronkonfiguration i grundtillståndet i själva verket är 5s14d4. Vi kan rationalisera denna observation genom att säga att den elektron-elektronavstötning som uppstår vid parning av elektronerna i 5s-banan är större än energiluckan mellan 5s- och 4d-banorna. Det finns ingen enkel metod för att förutsäga undantagen för atomer där storleken på repulsionerna mellan elektroner är större än de små skillnaderna i energi mellan underskalor.