Arean av en oregelbunden polygon

Denna artikel beskriver en enkel lösning på ett geometriskt problem, ett problem som jag finner beskrivet på alltför komplicerade sätt på nätet. Problemet går ut på att beräkna arean och omkretslängden för en tvådimensionell, sluten figur som en planritning av ett rum, eller en tomt, eller någon annan tvådimensionell avgränsad figur (en ”oregelbunden polygon”), oavsett hur komplicerad den är.

Jag gör verkligen inte anspråk på att vara originell när det gäller den här metoden. Versioner har funnits sedan Gauss tid eller tidigare. Men de flesta artiklar på nätet beskriver metoden på onödigt komplicerade sätt. Bland referenserna finns Wikipedias artikel Shoelace Formula, en liknande komplex metod i artikeln Polygon och ett antal artiklar som verkar vara mer beräknade för att demonstrera författarens lärdom än för att tillhandahålla det minst komplexa utförandet av metoden. Denna artikel (PDF) visar ett av de minst komplexa (men ingalunda enkla) uttrycken:

(1) $A = \frac{1}{2} \left\{ \left|\begin{array}{cc} x_0 & x_1 \\ y_0 & y_1\\\end{array} \right| + \left|\begin{array}{cc} x_1 & x_2 \\ y_1 & y_2\\\ \end{array} \right| + \left|\begin{array}{cc} x_2 & x_3 \\ y_2 & y_3\\ \end{array} \right| + … + \left|\begin{array}{cc} x_{n-2} & x_{n-1} \\ y_{n-2} & y_{n-1}\\\end{array} \right| + \left|\begin{array}{cc} x_{n-1} & x_0 \\ y_{n-1} & y_0\\\end{array} \right| \right\}$

Där $x_n,y_n$ är en polygonspets uttryckt i kartesiska koordinater, och $\left|\begin{array}{cc} x_0 & x_1 \\ y_0 & y_1\\ \end{array} \right|$ hänvisar till en determinant, med värdet $x_0 \times y_1 – y_0 \times x_1$

Du ska inte låta dig avskräckas av ovanstående redogörelse – det är lättare att använda den här metoden än att förstå dess matematiska underlag. När jag forskade i den här artikeln hittade jag ett oändligt antal svar på elevers förfrågningar som var så komplicerade att de omöjligen kunde ha upplyst eleven. I den här artikeln kommer jag att göra allt jag kan för att göra den här metoden så enkel och lättillgänglig som möjligt.

Metoden är lättast att uttrycka som en algoritm:

• En oregelbunden polygons hörn kan representeras som kartesiska koordinater:
• Varje koordinatpar behandlas i en algoritm för arealsammanräkning som ser ut så här:
  

  $A = A + \frac{(x_1 \times y_0 – y_1 \times x_0)}{2}$
  $A = A + \frac{(x_2 \times y_1 – y_2 \times x_1)}{2}$
  …

• Ett enkelt matematiskt uttryck för ovanstående skulle vara:
  

  (2) Oregelbunden polygonarea $\displaystyle A = \frac{1}{2} \sum_{i=m}^{n-1}{x_{i+1} \times y_i – y_{i+1} \times x_i}$

• OBS: I ekvation (2) slutar den genomgångna figuren med den sista uppgiften, den upprepar inte den första uppgiften som visas i ekvation (1) ovan. För mina syften, som förklaras nedan, är denna form avsiktlig – i en lantmäteriförrättning bör fältdata avsluta figuren, dvs. den sista posten bör vara lika med den första. I en sådan tillämpning skulle en automatisk stängning av figuren enligt ekvation (1) dölja fel som måste utvärderas.

  Användare kan föredra den form som visas i ekvation (1) ovan, för andra syften än att reducera data från lantmäteriet. För dessa ändamål kan man under bearbetningen helt enkelt omvärdera den första dataposten i slutet av traverseringen, eller tillhandahålla datamängder som upprepar den första dataposten som den sista.

• Här finns en komplett, fungerande Python-funktion:
  

  def find_area(array): a = 0 ox,oy = array for x,y in array: a += (x*oy-y*ox) ox,oy = x,y return a/2 

• Array-argumentet ovan är en uppsättning kartesiska koordinater $x,y$, dvs.e. ((10,10),(10,20),(20,20),(20,10),(10,10)). Lägg märke till att den första dataposten upprepas i slutet av denna datamängd.

• Här är en något mer komplex Python-funktion som beräknar både area och omkretslängd:
  

  def find_area_perim(array): a = 0 p = 0 ox,oy = array for x,y in array: a += (x*oy-y*ox) p += abs((x-ox)+(y-oy)*1j) ox,oy = x,y return a/2,p 

• Ännu en påminnelse: För båda ovanstående kodexempel, i andra tillämpningar än reduktion av lantmäteridata, bör den tillhandahållna datamängden innehålla en kopia av den första dataposten som den sista, dvs.dvs. figuren bör uttryckligen stängas.

• Jag valde Python för dessa exempel eftersom en Pythonlistning maximerar den algoritmiska innebörden samtidigt som den minimerar cruft.

• Ovanstående funktioner kan lätt konverteras till andra språk, nästan direkt – förutom den ovan visade omkretsuppsumman, som utnyttjar det faktum att Python stöder komplexa tal. För språk som inte stöder komplexa tal kan man skapa perimeterresultatet på följande sätt:

  C/C++: p += sqrt(pow(x-ox,2)+pow(y-oy,2));

  Java: p += Math.sqrt(Math.pow(x-ox,2)+Math.pow(y-oy,2));

• Formellt är omkretslängden summan av vektorernas magnituder:
  

  (3) Omkretslängd $\displaystyle P = \sum_{i=m}^{n-1}{\sqrt{(x_{i+1}-x_i)^2 + (y_{i+1}-y_i)^2}}$

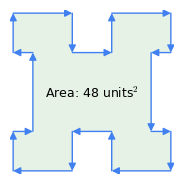
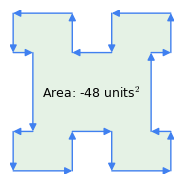Figur 1: Medurs vs. Vektorer moturs

Här är några viktiga egenskaper hos denna metod:

• Originalpunkten som väljs inom polygonen är irrelevant för antingen area- eller omkretsberäkningen, endast att figuren är sluten, dvs.D.v.s. att den sista koordinaten ska vara lika med den första.
• ”Klockslagsregeln”: Vektorernas ordning har betydelse – om omkretsen genomkorsas medurs är resultatet för arean positivt, om den genomkorsas moturs är det negativt (figur 1). Det är denna egenskap hos metoden som subtraherar arean av böjningar från en komplex figur som i figur 1 – ”böjningarna” representerar en traversering moturs inom polygonen.
• Många tillämpningar av denna metod använder ursprungliga datakällor som består av polära vektorer (ett exempel är juridiska beskrivningar från lantmäteriet), men denna metod kräver kartesiska koordinater. Konverteringen från polära till kartesiska koordinater är trivial, men det är viktigt att komma ihåg detta krav.
• För en korrekt arealberäkning bör den beskrivna polygonen vara en sluten figur – den sista koordinaten bör vara lika med den första. För tillämpningar som använder fältdata som består av längdvektorer som senare konverteras till kartesisk form är det en bra idé att jämföra den inledande och avslutande kartesiska koordinaten – de ska vara lika. Till exempel misslyckas äldre lantmäterier (före eran av billig datorkraft) regelbundet med detta test.

Denna sektion är en fullt fungerande area/perimeterdator som kan bearbeta inmatade datapar med kartesiska eller polära koordinater, eller lagstadgade lantmäteribeskrivningar. Välj bara en datatyp (kartesiska x,y-koordinater, polära m,θ-koordinater eller en juridisk beskrivning) och skriv in (eller klistra in) data i inmatningsområdet nedan. Du kan också välja exempel på datamängder för att bekanta dig med och öva.

På grund av säkerhetsproblem i webbläsaren, för att undvika överdrivet skrivande och för att importera stora mängder data från en annan källa, måste läsarna använda sitt systems klippbord. Det är bara att kopiera data till klippbordet i källprogrammet, klicka sedan på inmatningsområdet nedan och tryck på Crtl+A för att välja alla, Ctrl+V för att kopiera data från ett annat ställe och Ctrl+C för att kopiera dina egna inmatade data. De flesta webbläsare innehåller även klippbrädsfunktioner som menyalternativ.

Välj datatyp:

Kartesisk (x,y)

Polär (m,θ)

Undersökningsbeskrivning

Inmatningsområde för data: Välj alla: Ctrl+A | Kopiera: Ctrl+C | Klistra in: Ctrl+V

Diagramområde:

Ledsen – din webbläsare har inte stöd för den grafiska förmågan som denna funktion kräver –
överväg att installera Google Chrome eller Firefox.

Optioner:

Linjer

Pilar

Ursprung

Centrum

Längdenhet:

Linjebredd:

Omvänd

Resultat:Välj alla: Ctrl+A | Kopiera: Ctrl+C | Klistra in: Ctrl+V

Att datorn för area/perimeter har tre inmatningslägen:

• Kartesianska (x,y) koordinatpar:

  • Varje koordinat är en tvådimensionell position med en horisontell (x) och vertikal (y) del (en kartesisk koordinat).
  • Koordinaterna är inte kumulativa – var och en av dem beskriver självständigt sin plats.
  • Så en kvadrat skulle vara:
    • 0,0 (ursprung)
    • 0,100 (uppåt)
    • 100,100 (höger)
    • 100,0 (nedåt)
    • 0,0 (tillbaka till ursprunget)
  

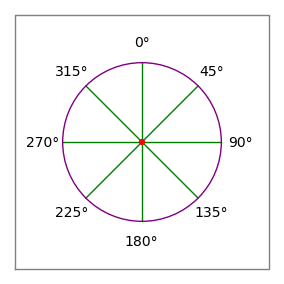  Figur 2: Kompassros

  • Kommanterna i exemplet ovan är endast avsedda att gruppera dataparren för läsaren – de har ingen betydelse för områdesdatorns dataanalysator.
  • Parseraren är tillräckligt robust för att ovanstående exempel kan klistras in i datorns datainmatningsområde och det kommer att fungera (prova).
  • Den enda begränsningen är att förklarande kommentarer inte kan innehålla siffror.

• Polära (m,θ) koordinatpar:

  • Varje koordinat består av ett avstånd och en vinkel i grader (en polär vektor).
  • Vinklarna följer kompasskonventionerna – 0 grader är uppåt eller ”norr”, 90 grader är till höger eller ”öster” (figur 2).
  • I motsats till den tidigare kartesianska formen är dessa koordinater kumulativa – varje ny vektor adderar till den nuvarande positionen.
  • Så en kvadrat skulle vara:
    • 100,0 (upp)
    • 100,90 (höger)
    • 100,180 (ner)
    • 100,270 (tillbaka till ursprunget)
  • Som tidigare fungerar exemplet om det klistras in i datorns datainmatningsfält och det polära läget är valt.
  • Observera om polarkoordinater att ursprunget är implicit och förinställt på x = 0, y = 0.
  

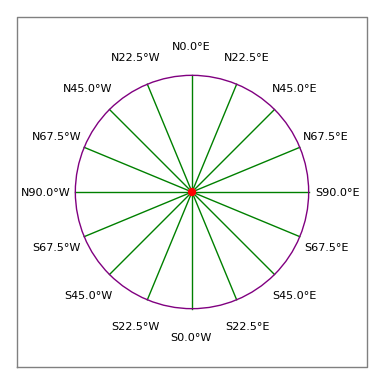  Figur 3: Lantmätarens kompassros

• Rättslig beskrivning:

  • Först en förklaring av förhållandet mellan valet av ”längdenheter” och resultatdisplayen:
    • För varje polygon beräknas en lista med arealeresultat med hjälp av en fast uppsättning gemensamma arealenheter (fot2, meter2 osv.). För att denna arealförteckning ska vara meningsfull måste de ingående längdenheterna vara kända.
    • I kartesiskt och polärt läge har dataposter inga enheter, så användaren väljer själv vilka enheter som ska tilldelas längderna. När användaren ändrar längdenheterna ändras alltså områdesvärdena, längdenetiketterna, men inte längdvärdena.
    • I Survey-läge innehåller den juridiska beskrivningen längdenheter (fot, meter osv.), vilket innebär att längdenheterna är fördefinierade av källan. När användaren ändrar längdenheterna ändras alltså längdenetiketter och längdvärden, inte områdesvärden.
  • Parseringen av undersökningsbeskrivningar är den överlägset minst tillförlitliga av de tre dataparseringsmetoderna – den är mer ett experiment än en robust metod för datakonvertering.
  • Jag skrev denna parser genom att ladda ner ett antal lagstadgade beskrivningar (som tillhandahålls som exempel i kalkylatorn ovan) och justera parserns kod tills alla kunde avkodas med framgång.

  Kriterier för ”framgång” var att resultatet skulle ha samma kvadratyta som beskrivningen påstår, och att figuren ”stämmer”.

  • Uttrycket ”closure”, och särskilt ”error of closure”, används inom lantmäteriarbete för att beskriva i vilken grad slutpunkten av lantmäteriets traversering är lika med utgångspunkten. Detta är sällan sant i verkligheten – fel i slutenhet beror vanligtvis på fel i fältarbetet, och äldre undersökningar, som publicerades före införandet av billig datorkraft, tenderar att ha ganska dåliga slutenheter samt vilt felaktiga uppskattningar av kvadratytan.
  • En lagstadgad beskrivning är ett formellt sätt att beskriva en tomt – dess form och syntax har uppstått under årtionden genom ömsesidigt accepterade, något godtyckliga, konventioner som delas av lantmätare.
  • För denna area/perimeter-dator måste de inmatade uppgifterna följa vissa strikta konventioner som vissa, men inte alla, lagstadgade beskrivningar följer. De viktigaste delarna är följande:
    • Fraktionen ”startpunkt”, som skiljer ett visst preliminärt innehåll från det som beskriver måtten på det beskrivna paketet. I vissa dokument står det ”True point of beginning”, i andra står det ”Real point of beginning” och i vissa står det ”Point of beginning”. En framgångsrik parser måste ta bort innehållet före denna fras och behålla allt efter den.
    • En serie fraser som beskriver en speciell typ av polarvektor som används av lantmätare:
      • Ordet ”Nord” eller ”Syd”, eller dess förkortning ”N” eller ”S”.
      • Därefter en vinkel uttryckt i grader, minuter och sekunder.
      • Därefter ordet ”Öst” eller ”Väst”, eller dess förkortning ”E” eller ”W”.
      • Därefter ett avstånd.
      • Därefter en avståndsenhet – fot, meter osv.
• Här är några olika exempel på lantmätarvektorer från exemplet på rättsliga beskrivningar:
  • N 2°0’0″ W – 63,50 fot
  • N90°00’00 ”W Längs en linje som är parallell med nämnda norra linje på ett avstånd av 6,00 fot
  • Nord 0°06’O0″ västerut på en sträcka av 554.86 fot
  • S. 22 grader 41′ 55″ Ö. 174,10 fot
• Observera att ovanstående exempel har olika syntax. Det finns många juridiska beskrivningar som den här parseraren inte lyckas avkoda, bara för att jag inte har försökt införliva deras syntax. Men det är viktigt att tillägga att en verkligt robust parser för den mängd juridiska beskrivningar som finns måste vara lika smart som Watson.
• Användare av denna dator för område/perimeter kanske vill undvika att skicka in juridiska beskrivningar i klartext och hoppas att parsern kommer att räkna ut det. Om du vill göra direkta handinmatningar (eller skapa en lista över traverser på andra ställen för import) kan du använda denna konvention:
  • Håll i minnet att en godtagbar traverse-post består av ordet ”North” eller ”South”, eller bokstaven ”N” eller ”S”, följt av upp till tre siffror som anger grader, minuter och sekunder för vinkeln, följt av ordet ”East” eller ”West” eller bokstaven ”E” eller ”W”, följt av ett avstånd, följt av en avståndsenhet.
  • En godtagbar uppgift skulle alltså vara ”N 30 15 45 W 100 fot”, vilket innebär ett travers på 100 fot som pekar 30 grader, 15 minuter och 45 sekunder väster om norr (dvs. ungefär 330 kompassgrader, se figur 3).
  • Minuter och sekunder kan hoppas över om de är lika med noll, eller om posten är i decimalgrader eller grader och decimalminuter.
• Det är inte svårt att omvandla en utskriven juridisk beskrivning till sådana poster, och det finns ett antal sätt att upptäcka fel. När alla traverser har matats in, om figuren inte har något stängningsfel och rapporterar samma kvadratyta som originalet, är chansen stor att inmatningarna är korrekta (eller att de har samma fel som den ursprungliga beskrivningen).
• Efter att ha matat in en laglig beskrivning på det här sättet, om det finns ett oacceptabelt stängningsfel eller om kvadratytan är felaktig, kom ihåg att originaldata kan vara felaktiga. Det finns hur många juridiska beskrivningar som helst som aldrig har kontrollerats mot en datormetod som denna, och som aldrig var korrekta.

När du bläddrar bland de kartesiska (x,y)-exemplen, lägg märke till de olika figurernas förhållande mellan area och omkrets. Den ”udda polygonen” har ett mellanliggande förhållande, cirkeln har det minsta förhållandet och Hilbert-rummet har det överlägset största förhållandet. Detta förhållande sträcker sig in i högre dimensioner, där en sfär är känd för att ha den största volymen per yta.

Om cirkelexemplet – det är en ”enhetscirkel”, en cirkel med radien ett. För det givna exemplet är arean ungefär $\pi$ och omkretsen ungefär $2\pi$, rätt värden för en enhetscirkel. För att dessa värden skulle vara mer än approximationer, för att vara exakt lika med $\pi$ och $2\pi$, måste antalet polygonsidor vara oändligt. Jag bestämde mig för att inte göra det 🙂

Exemplet med Hilbertrymden genererades med hjälp av en Sage-algoritm med ett blygsamt val av ordning (för att undvika att generera för mycket data). I princip kan ett Hilbert-rum ha ett oändligt förhållande mellan omkrets och area i två dimensioner, eller mellan yta och volym i tre dimensioner. För att se hur komplex en Hilbert-rymd kan bli, klicka här för att se en Hilbert-rymd av ordning 7.

Bemärk om Hilbert-exemplet att den beräknade arean är nära 1/2 för en 1×1-yta. I idealfallet, utan nödvändigheten att omvandla en linjetavla till en areatavla och med rätt algoritm, skulle ytan vara exakt 1/2 av den för en kvadrat med samma dimensioner.

Det polära inmatningsläget är mer eller mindre likvärdigt med sköldpaddsgrafik, om man byter ut noll grader mot ”uppåt”, 90 grader mot ”höger” osv. och om varje sväng- och förflyttningssekvens sammanfattas till ett enda kommando. Att använda det polära inmatningsläget är ett enkelt sätt att för hand konstruera en komplex form, eftersom avstånd och vinklar är lättare att hålla reda på än kartesiska koordinater.

Jag använde mig för första gången av den ovan beskrivna metoden för beräkning av lantmäteriområdet för flera år sedan när jag bodde på landsbygden i Oregon, omgiven av människor som behövde känna till arean och omkretsen på sina fastigheter. Jag stötte på många chockerande exempel där fastighetsmäklare skamlöst lurade människor som inte hade något sätt att ta reda på vad som pågick. Vid ett antal tillfällen beräknade jag en areal utifrån en juridisk beskrivning, bara för att upptäcka att garantihandlingens anspråk på areal var helt felaktigt – och alltid högre än verkligheten.

Vid ett tillfälle ombads jag att dela upp en fastighet i två lika stora delar och skapa juridiska beskrivningar för var och en av dem. Eftersom jag hade en nyinköpt Apple II (som hade samma processorkraft som en modern pennvässare) var detta mycket lätt – men när jag arbetade insåg jag att den totala arealen var fel med ungefär tre tunnland, ungefär 25 % av den totala arealen. Jag konfronterade titelbolaget, som fräckt svarade: ”Se här, där det står ’mer eller mindre’ i lagfarten.”

Vid ett annat tillfälle påbörjade jag ett markköp, men förvarnad av ovanstående erfarenhet bestämde jag mig för att när jag fick lagfarten, när jag fick lagfarten, skriva in den juridiska beskrivningen i mitt program för att se om arealangivelsen stämde. Men till min förskräckelse upptäckte jag att alla äganderättsförsäkringar för skiftena i den sektionen hade samma juridiska beskrivning – av den först undersökta fastigheten. Det visade sig att fastighetsutvecklingsföretaget hade beslutat att spara pengar genom att mäta bara en av de dussintals tomter som erbjöds till försäljning och ta med den juridiska beskrivningen i alla äganderättsförsäkringar. De var säkra på att de skulle komma undan med det – vem vet trots allt något om matematik?

Efter att ha diskuterat med fastighetsbolaget och byggherren och försökt övertala dem att betala för undersökningar så att de juridiska beskrivningarna inte var artiga påhitt, gav jag upp och bestämde mig för att inte köpa marken. Det var som att ta reda på hur korv tillverkas – man kan veta för mycket.

• 04.15.2013 Version 1.3. En detaljerad förklaring av standarddataformatet har lagts till, dvs. listor där den första datapunkten upprepas som den sista.
• 03.24.2013 Version 1.2. Ytterligare optimering av analysatorn för undersökningsbeskrivningar, tillägg av fler resultatdatafält.
• 03.23.2013 Version 1.1. Förbättrad parser för juridiska beskrivningar för att hantera fler typer av beskrivningar, lagt till väljare för längdenheter och en resultatlista över områden i gemensamma enheter.
• 03.22.2013 Version 1.0. Initial Public Release.