Between Borders

Har du någonsin laddat ner ett dokument eller fått en fil från en vän för att sedan få en dålig utskrift? Det finns många möjliga orsaker till sådana problem: olika typsnitt för skaparen och skrivaren, olika operativsystem och olika versioner av samma operativsystem som avslöjar begränsningar i de så kallade plattformsövergripande standarderna, olika skrivarmotorer, särskilt när man växlar mellan bläckstråle och laser, och så vidare.

En ofta förbisedd orsak till problem är dock olika pappersstorlekar. När människor i USA och Kanada sträcker sig efter ett pappersark för att skriva eller skriva ut på är chansen stor att de sträcker sig efter ett papper i Letter-storlek (även känt som US Letter), som mäter 8,5 x 11 tum. Med några få undantag sträcker sig människor överallt annars efter ett pappersark att skriva eller skriva ut på ett papper i A4-storlek, som mäter 210 mm x 297 mm.

En snabb omräkning mellan tum och millimeter visar att de två storlekarna inte är så olika:

	Millimetrar		Tummor
	Bredd	Längd	Bredd	Längd
A4	210.0	297.0	8.26	11.69
Letter	215.9	279.4	8.50	11.00

Och en skalrepresentation av varje sidstorlek förstärker närheten mellan de två pappersstorlekarna.

Vilket väcker frågan, varför skillnaden alls? Om båda storlekarna är godtyckliga, varför bry sig om att upprätthålla en skillnad. Svaren är långa och komplicerade och ligger till stor del utanför ramen för den här artikeln. I grund och botten handlar det dock om en sak: A4 är inte en godtycklig storlek.

A4 Beskrivet

A4 är en del av ISO 216-serien av relaterade pappersstorlekar som mer allmänt kallas för A-serien. Denna serie börjar med det stora A0-arket och en snabb titt på detta stora pappersark visar varför dessa olika ark har de storlekar de har.

A0-ark är 841 mm x 1189 mm. Återigen, uppenbarligen godtyckligt. Multiplicera dock de två siffrorna med varandra och det blir lite tydligare: 841 * 1189 = 999,949 mm i kvadrat eller 0,999949 m i kvadrat (dvs. en liten bit under en kvadratmeter papper). För alla praktiska ändamål innehåller ett A0-ark en kvadratmeter papper.

Så varför inte göra det till ett ark på 1 m x 1 m? På grund av ett annat icke godtyckligt övervägande: förhållandet mellan höjden och bredden på varje ark.

1189/841 = 1,413793103448276. Inte särskilt minnesvärt, om man inte råkar vara tillräckligt matematiskt intresserad för att se likheten mellan det och √2 (kvadratroten av 2, ett irrationellt tal som börjar så här: 1.414213562373095). Avrunda båda talen till fyra signifikanta siffror och du får samma värde: 1,414.

Så är förhållandet mellan formatet på ett A0-pappersark, återigen för praktiska ändamål, 1:1 i förhållande till kvadratroten av två eller 1:√2. Och återigen hör jag ropen: ”Än sen?”

Ett förhållande på 1:√2 är mer än ett matematiskt konstigt fenomen. Det har inget tjusigt namn, som det berömda gyllene snittet eller gyllene medelvärdet. Det har dock en smart egenskap. Dela en rektangel med sidorna 1:√2 längs den längsta sidan och den mindre rektangeln du skapar har samma längdförhållande. (Markus Kuhn föreslog i korrespondensen att vi skulle kalla förhållandet för Lichtenbergförhållandet, efter professor Georg Christoph Lichtenberg, den tyske upplysningsmannen som först föreslog förhållandet som en grund för pappersformat år 1786.)

Vi återvänder till förhållandet (namngivet eller inte) och dess smarta egenskap: om vi börjar med ett jättebra ark A0-papper:

Vi kan enkelt, och snabbt, härleda alla de andra storlekarna i A-serien genom att vika eller dela dem på detta sätt:

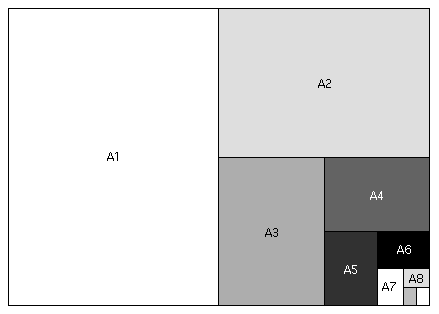
Mindre visuellt uttryckt är varje ark A-papper lika långt som nästa större ark är brett och hälften så brett som nästa större ark är långt. Det vill säga:

Bladnamn	Bredd (mm)	Längd (mm)
A0	841	1189
A1	594	841
A2	420	594
A3	297	420
A4	210	297
A5	148	210
A6	105	148
A7	74	105
A8	52	75

Det finns andra fördelar med detta förhållande mellan pappersstorlekar, inte minst när du vill skala en viss layout. Om du någonsin har undrat varför kopieringsmaskiner erbjuder ett alternativ för 71 % minskning behöver du inte undra mer: 0,71 är ungefär lika med (√2)/2 eller √0,5. Detta gör den perfekt för att minska en A3-layout till ett A4-ark eller en A4-layout till ett A5-ark eller, mer vanligt, för att minska två A4-ark sida vid sida – t.ex. i en journal – snyggt och utan krångel till ett A4-ark. Det lika vanliga 141 %-alternativet är naturligtvis perfekt för att förstora från ett ark i A-serien till nästa (t.ex. från A4 till A3). Det viktigaste är att eftersom varje ark har samma bildförhållande behåller objekten sina relativa former: fyrkanter blir inte rektanglar och cirklar blir inte ellipser.

Om inte annat gör detta konstanta förhållande A-papper enklare att arbeta med än äldre pappersstorlekar som Brief (13˝ x 16˝, och källan till de ”briefs” som advokater fortfarande använder) eller Foolscap (27˝ x 17˝) och dess derivat i nästan bokstavsstorlek, Foolscap Quarto (13˝ x 17˝).5˝ x 8,5˝, vanligen om än felaktigt kallad ”Foolscap”).

Om man lägger till en tydlig koppling till det metriska (eller, mer korrekt, SI-) mätsystemet är det ganska lätt att förstå den ökande populariteten för A-papper: i takt med att världen sakta men säkert har övergått till det metriska systemet har A-papper blivit mer populärt. I Australien till exempel antogs det metriska systemet officiellt 1974, samma år som papper i A-serien (och relaterade serier som C-serien för kuvert) började bli standard.

US Letter Described

Den tydliga kopplingen till det metriska systemet är också en delförklaring till den fortsatta användningen av papper i Letter-storlek i USA och Kanada. USA är nästan det enda land som återstår som inte har bytt från icke-metriska mått, vilket gör de särskilda fördelarna med A4 mindre uppenbara. Även om de amerikanska pappersstorlekarna är så godtyckliga som det ibland hävdas är de inte omöjliga att arbeta med.

Det finns ingen härledd utgångspunkt (motsvarande 1 kvadratmeter för A0) för de amerikanska pappersstorlekarna, men de två populäraste storlekarna – Letter och Tabloid – är en del av en gammal standard från American National Standard Institute för tekniskt ritpapper. Denna standard (ANSI/ASME Y14.1) hade fem pappersstorlekar som pendlade fram och tillbaka mellan två olika formatförhållanden:

Bladnamn	Bredd (˝)	Längd (˝)	Aspektförhållande
A (Brev)	8.5	11.0	1.294
B (Tabloid)	11.0	17.0	1.545
C	17.0	22.0	1.294
D	22.0	34.0	1.545
E	34.0	44.0	1.294

Detta är inte lika elegant eller bekvämt som papper från A-serien, men det är inte särskilt svårt att förstora och förminska vissa layouter samtidigt som man behåller de interna förhållandena. Det är bara att hoppa över en pappersstorlek när man reser i endera riktningen.

Det är värt att notera att inget av bildförhållandena har några särskilda matematiska egenskaper. Och att det finns två bildförhållande är inte förvånande: vik någon rektangel på mitten som inte har sidor i förhållandet 1:√2 och den mindre rektangelns sidor kommer att stå i ett annat förhållande till varandra. Vik den mindre rektangeln på mitten igen och den tredje rektangeln kommer att ha sidor i samma förhållande som den du började med.

Denna enkla egenskap är anledningen till att rektanglar med sidor i förhållandet 1:√2 är så smarta: de är de enda där de två förhållandena som du får genom att vika fram och tillbaka är ekvivalenta och utbytbara.

Och själva nyttan av denna utbytbarhet är anledningen till att jag tror att äldre pappersstorlekar, som US Letter, så småningom kommer att försvinna, även i USA. Den nuvarande versionen av ANSI-standarden som nämns ovan – ANSI/ASME Y14.1m-1995 – erkänner till exempel de äldre pappersstorlekarna endast för äldre ändamål och fastställer papper i A-serien som den föredragna amerikanska standarden för tekniska ritningar.

För övrigt har jag förstått att A-papper – särskilt A4-papper – långsamt håller på att bli normen på amerikanska högskolor och universitet, om inte annat för att göra det lättare för studenter och personal att fotokopiera artiklar från tidskrifter (oundvikligen i A4-storlek).

Till sist kräver globaliseringen sin tribut: Amerikanska företag som gör affärer med myndigheter utanför USA (särskilt inom EU) upptäcker att de måste lämna in förslag, anbud, diagram och så vidare på A-papper.

Söka efter rätt filformat

Detta är bra, men löser inte det omedelbara problemet: hur kan någon som i dag utformar dokument som skall användas i Nordamerika och resten av världen se till att deras utformning inte misslyckas på grund av skillnaderna mellan papper i A4- och Letter-format?

För det första, och med hänvisning till alla andra potentiella orsaker till problem som nämns ovan, skicka eller distribuera inte dokument som är beroende av externa faktorer för att visas och skrivas ut korrekt. Så inga Word-dokument, inga Quark XPress-dokument, inga PageMaker-filer, inga AppleWorks-filer och så vidare.

Även om du är säker på att den person som tar emot dina filer har samma version av samma program, alla typsnitt som du har använt och använder samma skrivare, är inget av dessa filformat säkert att skicka över gränserna för olika pappersstorlekar. De misslyckas på denna sista punkt eftersom de fortfarande är beroende av externa faktorer för att visas och skrivas ut.

Till exempel kommer ett Word-dokument som formaterats med 25 mm marginaler på Letter-format papper att återge texten som det innehåller när det öppnas på en dator som som standardmässigt visar dokument på A4-format. Även rak prosa som körs i en enda kolumn kommer att återfalla under sådana omständigheter. Något mer komplext (t.ex. en blandning av text och bilder eller ett manuskript) kommer med största sannolikhet att visas felaktigt i mottagarsidan under sådana förhållanden.

(Jag skulle till och med gå så långt som att föreslå att det är uteslutet att skicka diskreta textfiler (dvs. en textfil som sänds som en bilaga till ett e-postmeddelande i stället för att ingå som en del av meddelandekroppen), om inte annat så på grund av det fortfarande kvarstående problemet med ”vilken radslut de använde”, men det är ett separat problem.)

Listan över dokumenttyper som inte bör skickas är ganska lång. Listan över dokumenttyper som kan skickas är ganska kort: råa PostScript-filer och Adobe Acrobat-filer (alias ”pdf”).

Båda filformaten kodar och fixerar de rumsliga relationerna mellan enskilda element på en sida. Att generera råa PostScript-filer är relativt enkelt: ställ in datorn så att den skriver ut till en PostScript-kapabel skrivare (även om du inte har någon tillgänglig) och ”skriv sedan ut” ditt dokument till en fil. Filen som produceras på detta sätt är säker att skicka. Tyvärr kan filen inte visas på en skärm utan att man ägnar sig åt en del allvarlig nörderi och kan bara skrivas ut på ett tillförlitligt sätt genom att skicka den till en PostScript-kapabel skrivare.

Acrobat-filer: det bästa av det sämsta

Vilket som standard gör Acrobat-filer till det bästa alternativet. Jag säger ”som standard” eftersom Acrobat-filer inte skulle vara mitt förstahandsval. Filformatet är bara halvöppet och Acrobat-filerna är större än vad jag skulle vilja ha dem i förhållande till den mängd information som är kodad i dem. Det finns också en liten kostnadsfråga.

När du har köpt ett exemplar av Word kostar det inte mer att skapa ett Word-dokument. Detsamma gäller för andra verktyg för skapande av dokument som Quark XPress, WordPerfect, PageMaker och så vidare.

Däremot marknadsförs eller säljs Acrobat inte som ett verktyg för skapande av dokument. Adobe beskriver Acrobat som:

ett universellt filformat som bevarar alla teckensnitt, formatering, grafik och färger i alla källdokument, oavsett vilket program och vilken plattform som använts för att skapa det

Grovt sett är Acrobat en efterföljare till PostScript. Liksom PostScript är Acrobat ett programmeringsspråk som är utformat för att exakt definiera var på en sida objekt ska placeras. Dessutom innehåller Acrobat några ibland smarta verktyg för att omvandla dessa väldefinierade sidor till formulär som kan hantera nya data i farten.

Från perspektivet för någon som vill distribuera formaterade sidor är den viktigaste skillnaden mellan Acrobat och PostScript Adobe Acrobat Reader. Medan Adobe tar betalt för att inkludera en PostScript-tolkare i sina produkter (en del av anledningen till att PostScript-skrivare kostar mer än skrivare som inte är PostScript-skrivare) är Acrobat-tolkaren (dvs. Acrobat Reader) gratisprogram, tillgänglig för nedladdning och ingår som en del av nästan varje dator eller operativsystem som köps.

Det låter ju jättebra, tills man måste skapa en Acrobat-fil och inser att Adobe bara har ändrat vem de tar betalt för. PostScript-filer är gratis att skapa (PostScript-skrivardrivrutiner är gratis) men kostar pengar att visa (PostScript-skrivare är dyra jämfört med skrivare som inte är PostScript-skrivare).

Acrobat-filer är gratis att visa (Acrobat Reader är gratis) men kostar pengar att skapa (inga Adobe-verktyg för att skapa Acrobat-filer är gratis).

Skapa Acrobat-filer

Adobe erbjuder flera verktyg för att skapa Acrobat-filer, till att börja med en webbaserad tjänst som du kan prova utan kostnad och prenumerera på för 10,00 USD/månad eller 100 USD/år. Denna tjänst är endast tillgänglig för invånare i USA och Kanada.

För resten av oss (och för amerikaner och kanadensare som föredrar en förskottsbetalning framför en löpande prenumerationsavgift) finns Adobe Acrobat, som Adobe tar 250,00 US-dollar för, men som kan köpas från återförsäljare för cirka 220,00 US-dollar.

Adobe erbjuder också en rad dyrare produkter i Acrobat-familjen som är utformade för att tillgodose behoven i företagens arbetsflöden.

Och för de äventyrliga finns det olika tredje parter som drar nytta av att Acrobat är halvöppet för att tillhandahålla verktyg för skapande av Acrobat utan Adobes formella godkännande. Ett bra ställe att börja gräva efter information om sådana verktyg är The PDF Zone.

Förberedelse av filer för Acrobat

Så, med det slutgiltiga filformatet bestämt, och verktyg för att skapa nämnda format i handen, är det dags att ta itu med dokumentlayouten.

Vid första anblicken verkar det relativt enkelt: begränsa dina mönster och layouter till ett område som båda storlekarna kan rymma.

Om du placerar ett A4- och ett Letter-format papper ovanpå varandra, så att deras övre vänstra hörn nuddar varandra, är skillnaderna mellan de två arken uppenbara: Letter är bredare än A4; A4 är längre än Letter. Så för att en design eller layout ska få plats på båda arkstorlekarna får den inte vara bredare än A4 och inte längre än Letter. Med andra ord är gränserna för en design eller layout som passar säkert på båda bladstorlekarna bredden på ett A4-ark (210 mm eller 8,27˝) och längden på ett Letter-ark (11˝ eller 279,4 mm). Tyvärr är det inte riktigt så enkelt.

Tag ett enda A4-ark och använd de standardmarginaler på 25 mm (ca 1˝) som de flesta av oss använder när vi förbereder brev, rapporter, artiklar och liknande. Arbetsområdet – 160 mm x 247 mm – ligger väl inom de gränser som nämnts ovan. Fyll dock sidan med text och ett problem uppstår om dokumentet skickas till någon som använder Letter. Till exempel:

Texten ryms fortfarande på ett enda US Letter-ark, men den rinner ut över marginalerna. När en Letter-användare skriver ut filen kommer sidan antingen inte att skrivas ut ordentligt (eftersom en del av texten är placerad i en del av arket som inte kan skrivas ut) eller så kommer den att skrivas ut på en andra sida. Det andra resultatet är bättre, men ingetdera är önskvärt och det andra är i alla fall beroende av alltför många okontrollerbara variabler.

För att undvika detta problem är det enda alternativet för A4-användare som delar dokument med Letter-användare att öka sina nedre marginaler till 45 mm. Detta garanterar att texten på deras sidor inte kommer att sträcka sig in i den förbjudna zonen när den visas och skrivs ut av personer som fortfarande använder Letter. För att återigen visa snarare än berätta:

Vid övergång till liggande format är det Letter-användare som måste justera de nedre marginalerna. Med en standardmarginal på 25 mm på alla sidor kommer en liggande layout som ser bra ut på Letter-papper in i farozonen på A4:

Lägg till en extra marginal på 6 mm (ca 0.2˝) till den nedre marginalen och problemet undviks:

De layouter som presenteras i miniatyren ovan är medvetet enkla, men de föreslagna marginalförändringarna bör fungera även med mer komplicerade rutnätbaserade layouter. Problem kan och kommer dock att uppstå med layouter som är uppbyggda kring en centrumaxel i stället för ett av de traditionella rutorna.

En layout som är uppbyggd kring endast en centrumaxel bör ändå kunna visas och skrivas ut på ett acceptabelt sätt över alla pappersstorleksgränser med lämpliga marginaljusteringar. En enkel affisch i viktoriansk stil, till exempel, som är uppbyggd längs den vertikala axeln i stående läge:

En närmare titt avslöjar ett mindre problem med visningen. Designen är perfekt centrerad på A4-bladet men lite felplacerad på det amerikanska brevbladet. En oundviklig konsekvens av två saker: 1) A4 och US Letter är inte lika breda och 2) nästan alla verktyg för att lägga upp och presentera data digitalt använder sidans övre vänstra hörn som referenspunkt för att bestämma var objekten ska visas på sidan.

Samma problem kommer att uppträda med konstruktioner som är uppbyggda runt den vertikala axeln i liggande läge. Om till och med dessa mindre visuella fel är oacceptabla finns det inget annat alternativ än att förbereda två versioner av en design (t.ex. en US Letter- och A4-version eller en US Tabloid- och A3-version). Design som byggs runt både den vertikala och horisontella centrala axeln kommer nästan säkert att behöva förberedas både amerikanska och icke-amerikanska versioner i vilket fall som helst.

Underlätta problemet till att börja med

Om allt detta verkar vara ett problem som du skulle vara bra utan, välkommen till klubben. Tyvärr är de enda aktuella alternativen till att erkänna och ta itu med problemet:

1. ignorera det och irritera och/eller förlora kundkretsen hos personer som använder en annan sidstorlek än du.

2. övertala USA (och Kanada) att överge sina olika imperiala mätsystem och helhjärtat övergå till SI-systemet (eller det metriska systemet, för att använda den mindre formella termen).

De flesta människor kommer att sluta med att ignorera problemet. Detta är bara ett irriterande fel i uppförandet för människor som delar dokument av icke-kommersiella skäl, som oftast förlåts eller åtminstone inte kommenteras av den drabbade parten.

Och trots omfattningen är det ett vanligt förekommande kommersiellt fel eftersom den förlorade affären döljs av de relativa storlekarna på de två stora ekonomier som berörs: USA och EU. En person som är framgångsrik inom den ena sfären kan ignorera den andra och inte märka de förlorade intäkterna.

Vad gäller det andra alternativet, och trots min dämpade optimism ovan, ser jag inte att det kommer att inträffa inom den närmaste framtiden. En övergång genom beslut (som skedde framgångsrikt i Australien från och med 1974) är ytterst osannolik och den långsamma osmosen av metriska termer i det amerikanska livet har ännu inte nått det stadium där sådana mått ersätter sina imperiala motsvarigheter.

Därmed är vi kvar där vi började: vi har att göra med två något olika pappersstorlekar och alla de olägenheter som följer av dessa skillnader.