Faktoriella tal finns överallt i kombinatoriken eftersom det är där de har sitt ursprung. Faktorn skapades som ett sätt att uttrycka antalet arrangemang av en grupp objekt, som vi naturligtvis hittar genom att använda, i sin mest grundläggande form, multiplikationsregeln för att räkna.
Faktorn är ett slags inofficiell operation för multiplikationsregeln för att räkna.
Varför nollfaktorn är lika med 1
Det är här som det blir knepigt, för om vi bara tänker på faktorn i den kontext som de vanligtvis definieras i, dvs.dvs. ”produkten av alla positiva heltal som är mindre än eller lika med talet”, så är det som att gå in i en mur.
De flesta människor kommer att säga att 0! är definierat som 1, och om du frågar varför säger de bara ”för att det är definierat som ett”.
Ja, det är ganska frustrerande. Det är den matematiska motsvarigheten till att fråga dina föräldrar varför du måste följa någon godtycklig regel som de har hittat på och få svaret: ”för att jag har sagt det.”
Och även om det kan vara en accepterad föräldrateknik är det ett uselt sätt att lära sig matematik. Så vad är problemet? Hur kom vi fram till att nollfaktorn är lika med ett?
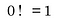
En intuitiv förståelse
Håller du ihåg hur vi sa att faktorn har sitt ursprung i den matematiska operationen att hitta antalet permutationer eller arrangemang av en mängd? (Observera: inte permutationerna av en mindre mängd från en större mängd, utan bara arrangemangen av en given mängd.)
Nollfaktorn kan ses som antalet arrangemang av noll element i en mängd, även kallad den tomma mängden {}. (Om du någonsin har studerat mängder, kanske i grundläggande statistik eller diskret matematik, är du förmodligen bekant med begreppet tom mängd. Det är bokstavligen mängden av ingenting.)
Om jag nu frågade dig hur många arrangemang det finns av en sak skulle du svara 1 eftersom det bara finns ett sätt att arrangera en sak. Samma idé följer här. Vår ”en sak” är den tomma mängden, och antalet arrangemang av den tomma mängden är ett. Så är det. Det är därför 0! är lika med 1.
Hur man förenklar faktoriella uttryck
Nu när vi har grunderna bakom oss är det dags för kärnan i vår faktoriella handledning: att förenkla.
Det bästa sättet att se matematik är i handling. Så här är jag för att gå igenom de sex problem som visas i bilden högst upp i det här inlägget! Vi börjar trevligt och enkelt, går sedan över till kombinationsformeln med siffror och sedan variabler och avslutar med några knepigare faktorialuttryck.
❤ HÅLL DIG INKOPPLAD ❤
Missa inte ett slag, eller ett matematiskt problem!