Ecuaciones de SHM
Consideremos un bloque unido a un muelle sobre una mesa sin fricción (Figura \(\PageIndex{3}\). La posición de equilibrio (la posición en la que el muelle no está ni estirado ni comprimido) está marcada como x = 0 . En la posición de equilibrio, la fuerza neta es cero.
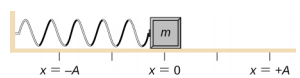
Se trabaja sobre el bloque para sacarlo hasta una posición de x = + A, y luego se libera del reposo. La posición x máxima (A) se llama amplitud del movimiento. El bloque comienza a oscilar en SHM entre x = + A y x = -A, donde A es la amplitud del movimiento y T es el período de la oscilación. El periodo es el tiempo de una oscilación. La figura \(\PageIndex{4}\a) muestra el movimiento del bloque mientras completa una oscilación y media después de la liberación.
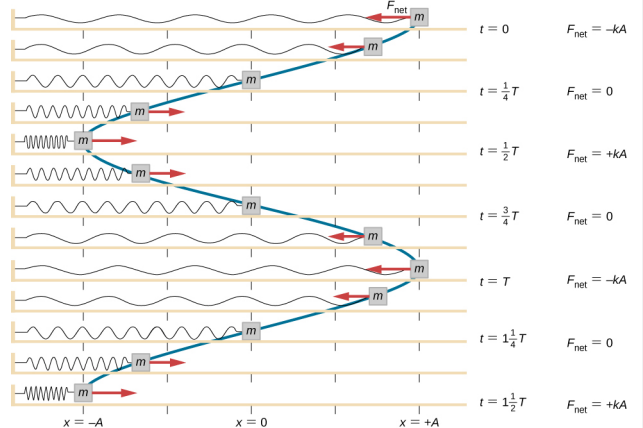
\️
La ecuación para la posición en función del tiempo \(x(t) = A\cos( \omega t)\️) es buena para modelar datos, donde la posición del bloque en el tiempo inicial t = 0,00 s está en la amplitud A y la velocidad inicial es cero. A menudo, cuando se toman datos experimentales, la posición de la masa en el tiempo inicial t = 0,00 s no es igual a la amplitud y la velocidad inicial no es cero. Considere 10 segundos de datos recogidos por un estudiante en el laboratorio, que se muestra en la Figura \ (\PageIndex{6}\).
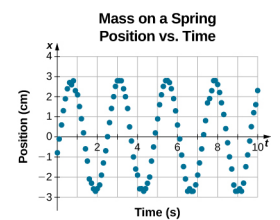
Los datos de la Figura \(\PageIndex{6}\} todavía puede ser modelado con una función periódica, como una función coseno, pero la función se desplaza a la derecha. Este desplazamiento se conoce como desplazamiento de fase y se suele representar con la letra griega phi (\(\phi\)). La ecuación de la posición en función del tiempo para un bloque sobre un muelle se convierte en
\
Esta es la ecuación generalizada para SHM donde t es el tiempo medido en segundos, \(\omega\) es la frecuencia angular con unidades de segundos inversos, A es la amplitud medida en metros o centímetros, y \(\phi\) es el desplazamiento de fase medido en radianes (Figura \(\PageIndex{7}\)). Cabe señalar que debido a que las funciones seno y coseno difieren sólo por un desplazamiento de fase, este movimiento podría ser modelado utilizando la función coseno o seno.
La velocidad de la masa sobre un muelle, oscilando en SHM, se puede encontrar tomando la derivada de la ecuación de posición:
\
Debido a que la función seno oscila entre -1 y +1, la velocidad máxima es la amplitud por la frecuencia angular, vmax = A\(\omega\). La velocidad máxima se produce en la posición de equilibrio (x = 0) cuando la masa se desplaza hacia x = + A. La velocidad máxima en sentido negativo se alcanza en la posición de equilibrio (x = 0) cuando la masa se desplaza hacia x = -A y es igual a -vmax.
La aceleración de la masa sobre el muelle puede hallarse tomando la derivada temporal de la velocidad:
\