Calcular ΔS a partir de ciclos termodinámicos
También podemos calcular un cambio de entropía utilizando un ciclo termodinámico. Como aprendiste anteriormente, la capacidad calorífica molar (Cp) es la cantidad de calor necesaria para elevar la temperatura de 1 mol de una sustancia en 1°C a presión constante. Del mismo modo, Cv es la cantidad de calor necesaria para elevar la temperatura de 1 mol de una sustancia en 1°C a volumen constante. El aumento de la entropía con el aumento de la temperatura en la figura \PageIndex{2}\N es aproximadamente proporcional a la capacidad calorífica de la sustancia.
Recordemos que el cambio de entropía (ΔS) está relacionado con el flujo de calor (qrev) por ΔS = qrev/T. Dado que qrev = nCpΔT a presión constante o nCvΔT a volumen constante, donde n es el número de moles de sustancia presente, el cambio de entropía para una sustancia cuya temperatura cambia de T1 a T2 es el siguiente:
Como descubrirás en cursos de matemáticas más avanzados que los que se requieren aquí, puede demostrarse que esto es igual a lo siguiente:Para un repaso de los logaritmos naturales, ver Habilidades Esenciales 6 en el capítulo 11 «Líquidos».
De manera similar,
\
Por lo tanto, podemos usar una combinación de mediciones de la capacidad calorífica (ecuación 18.20 o ecuación 18.21) y valores medidos experimentalmente de las entalpías de fusión o vaporización si hay un cambio de fase (ecuación 18.18) para calcular el cambio de entropía correspondiente a un cambio en la temperatura de una muestra.
Podemos utilizar un ciclo termodinámico para calcular el cambio de entropía cuando el cambio de fase para una sustancia como el azufre no puede medirse directamente. Como se observó en el ejercicio del ejemplo 6, el azufre elemental existe en dos formas (parte (a) en la figura \(\PageIndex{3}\)): una forma ortorrómbica con una estructura altamente ordenada (Sα) y una forma monoclínica menos ordenada (Sβ). La forma ortorrómbica (α) es más estable a temperatura ambiente, pero experimenta una transición de fase a la forma monoclínica (β) a temperaturas superiores a 95,3°C (368,5 K). La transición de Sα a Sβ puede describirse mediante el ciclo termodinámico que se muestra en la parte (b) de la figura (\PageIndex{3}\), en el que el azufre líquido es un intermedio. El cambio de entropía que acompaña a la conversión del azufre líquido en Sβ (-ΔSfus(β) = ΔS3 en el ciclo) no puede medirse directamente. Sin embargo, como la entropía es una función de estado, ΔS3 puede calcularse a partir del cambio de entropía global (ΔSt) para la transición Sα-Sβ, que es igual a la suma de los valores de ΔS para los pasos del ciclo termodinámico, utilizando la ecuación 1820 y los parámetros termodinámicos tabulados (las capacidades caloríficas de Sα y Sβ, ΔHfus(α), y el punto de fusión de Sα.)

Resolver para ΔS3 da un valor de -3,24 J/(mol-K). Como era de esperar para la conversión de un estado menos ordenado (un líquido) a uno más ordenado (un cristal), ΔS3 es negativo.
¿Cómo se miden las entropías
La entropía absoluta de una sustancia a cualquier temperatura por encima de 0 K debe determinarse calculando los incrementos de calor q necesarios para llevar la sustancia de 0 K a la temperatura de interés, y sumando después los cocientes q/T. Se necesitan dos tipos de mediciones experimentales:
- Las entalpías asociadas a cualquier cambio de fase que pueda sufrir la sustancia dentro del rango de temperatura de interés. La fusión de un sólido y la vaporización de un líquido corresponden a aumentos considerables en el número de microestados disponibles para aceptar energía térmica, por lo que, a medida que se producen estos procesos, la energía fluirá hacia un sistema, llenando estos nuevos microestados en la medida necesaria para mantener una temperatura constante (el punto de congelación o de ebullición); estas entradas de energía térmica corresponden a los calores de fusión y vaporización. El aumento de entropía asociado a la fusión, por ejemplo, es simplemente ΔHfusión/Tm.
- La capacidad calorífica C de una fase expresa la cantidad de calor necesaria para cambiar la temperatura en una pequeña cantidad ΔT , o más exactamente, en una cantidad infinitesimal dT . Así, el aumento de entropía provocado por el calentamiento de una sustancia en un rango de temperaturas que no abarca una transición de fase viene dado por la suma de las cantidades C dT/T para cada incremento de temperatura dT . Esto es, por supuesto, sólo la integral
\Nde la capacidad calorífica, que a su vez depende ligeramente de la temperatura, las determinaciones más precisas de las entropías absolutas requieren que se utilice la dependencia funcional de C con respecto a T en la integral anterior en lugar de una constante C.
Cuando esto no se conoce, se puede tomar una serie de mediciones de la capacidad calorífica sobre incrementos estrechos de temperatura ΔT y medir el área bajo cada sección de la curva.
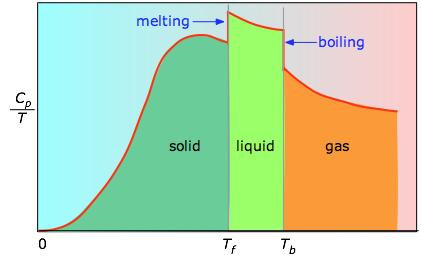
El área bajo cada sección del gráfico representa el cambio de entropía asociado al calentamiento de la sustancia a través de un intervalo ΔT. A esto hay que añadir las entalpías de fusión, vaporización y de cualquier cambio de fase sólido-sólido. Los valores de Cp para temperaturas cercanas a cero no se miden directamente, pero pueden estimarse a partir de la teoría cuántica.
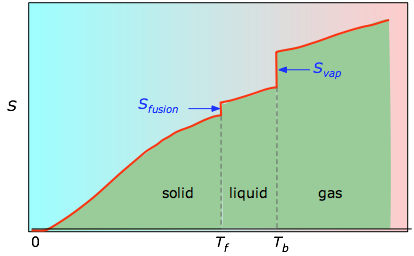
Las áreas acumuladas desde 0 K hasta cualquier temperatura dada (tomadas del gráfico experimental de la izquierda) se trazan entonces en función de T, y cualquier entropía de cambio de fase como Svap = Hvap / Tb se suma para obtener la entropía absoluta a la temperatura T.