Při pohledu do přírody jste si možná všimli složitých rostlin, jako jsou tyto:


Tato kapradina se skládá z mnoha malých listů, které se větví z jednoho většího.


Tato brokolice Romanesco se skládá z menších kuželovitých kuliček, které se spirálovitě obtáčejí kolem jedné větší.
Zpočátku vypadají jako velmi složité tvary – ale když se podíváte blíže, můžete si všimnout, že obě mají poměrně jednoduchý vzor: všechny jejich jednotlivé části vypadají úplně stejně jako celá rostlina, jen jsou menší. Stejný vzor se opakuje stále dokola v menších měřítkách.
V matematice tuto vlastnost nazýváme soběpodobnost a tvary, které ji mají, se nazývají fraktály. Jsou to jedny z nejkrásnějších a nejbizarnějších objektů v celé matematice.
Chceme-li vytvořit vlastní fraktály, musíme začít s jednoduchým vzorem a pak ho opakovat stále dokola, v menších měřítkách.
Jedním z nejjednodušších vzorů může být úsečka, z jejíhož jednoho konce se větví další dvě úsečky. Pokud tento vzor zopakujeme, budou mít obě tyto modré úsečky na svých koncích také další dvě větve.
Modrými tečkami můžete pohybovat a měnit tak délku a úhel všech větví. Poté pomocí posuvníku níže zvyšte počet iterací.
V závislosti na poloze větví můžete vytvořit zcela odlišné vzory – vypadající jako kapradí výše, strom nebo vnořené pětiúhelníky. Co dalšího můžete najít?
Dalším známým fraktálem je Sierpinského trojúhelník. V tomto případě začínáme s velkým rovnostranným trojúhelníkem a ze zbývajících částí opakovaně vyřezáváme menší trojúhelníky.
Všimněte si, že výsledný tvar se skládá ze tří stejných kopií sebe sama a každá z nich se skládá z ještě menších kopií celého trojúhelníku! Trojúhelník můžete zvětšovat donekonečna a vzory a tvary se budou stále opakovat.
Rostliny na začátku této kapitoly vypadají přesně jako fraktály, ale je zřejmé, že skutečné fraktály v reálném životě vytvořit nelze. Kdybychom stále dokola opakovali stejný vzor, stále menší a menší, dostali bychom se nakonec k buňkám, molekulám nebo atomům, které již nelze rozdělit.
Pomocí matematiky se však můžeme zamyslet nad vlastnostmi, které by skutečné fraktály „měly“ – a ty jsou velmi překvapivé…
Rozměry fraktálů
Nejprve se zamysleme nad rozměrem fraktálů. Čára má rozměr . Při zvětšení jejího měřítka o faktor 2 se její délka zvětší o faktor 21=2 . Je zřejmé!
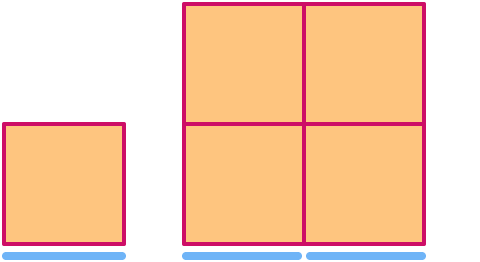
Čtverec má rozměr . Při jeho zmenšení o faktor 2 se jeho plocha zvětší o faktor 22= .
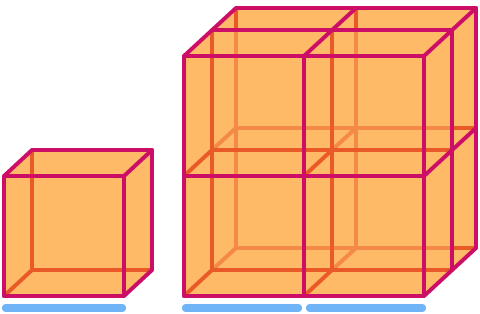
Krychle má rozměr . Při jejím zmenšení o faktor 2 se její objem zvětší o faktor 23= . Všimněte si, že větší krychle na obrázku se skládá z 8 kopií té menší!
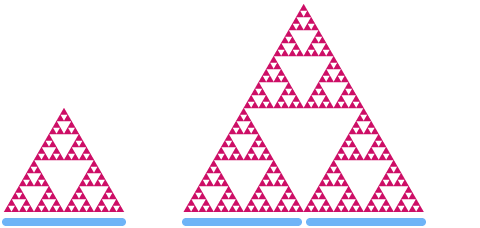
Nyní se podíváme na Sierpińského trojúhelník. Pokud jej zvětšíme o dvojnásobek, uvidíte, že jeho „plocha“ se zvětší o faktor .
Řekněme, že d je rozměr Sierpinského trojúhelníku. Použijeme-li stejný vzorec jako výše, dostaneme 2d=3. Jinými slovy, d = log23log32 ≈ 1,585…
Ale počkat… jak může mít něco rozměr, který není celé číslo? Zdá se to nemožné, ale je to jen jedna z podivných vlastností fraktálů. Ve skutečnosti je to to, co dává fraktálům jejich jméno: mají zlomkový rozměr.
Každou iterací odstraníme část plochy Sierpinského trojúhelníku. Kdybychom to mohli udělat nekonečně mnohokrát, nezbyla by nám vlastně žádná plocha: proto je Sierpinskiho trojúhelník něco mezi dvourozměrnou plochou a jednorozměrnou přímkou.
Ačkoli mnoho fraktálů je sobě podobných, lepší definice zní, že fraktály jsou tvary, které mají neceločíselný rozměr.
Kochova sněhová vločka
V přírodě existuje mnoho tvarů, které vypadají jako fraktály. Některé jsme již viděli na začátku této kapitoly u rostlin. Dalšími skvělými příklady jsou sněhové vločky a ledové krystaly:
Chceme-li vytvořit vlastní fraktální sněhovou vločku, musíme opět najít jednoduchý postup, který můžeme používat stále dokola.
Stejně jako u Sierpińského trojúhelníku začneme s jedním rovnostranným trojúhelníkem. Avšak místo toho, abychom v každém kroku odstraňovali menší trojúhelníky, přidáváme menší trojúhelníky podél hrany. Délka strany každého trojúhelníku je 131412 trojúhelníků v předchozím kroku.
Výsledný tvar se nazývá Kochova sněhová vločka, pojmenovaná po švédském matematikovi Helge von Kochovi. Opět si všimněte, že malé úseky hran sněhové vločky vypadají úplně stejně jako větší úseky.
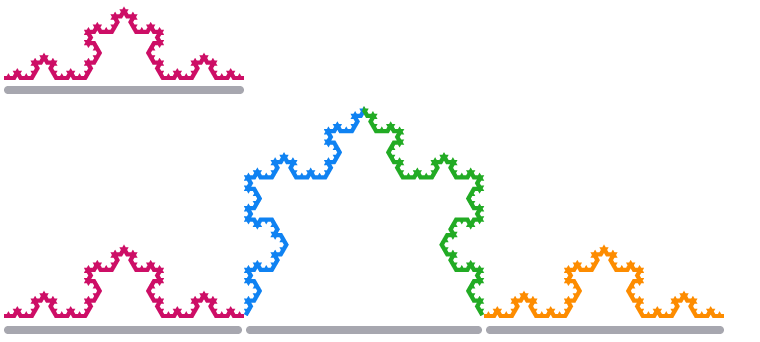
Když jednu úsečku hrany Kochovy sněhové vločky zmenšíme na trojnásobek, její délka se čtyřikrát zdvojnásobí.
Při použití stejného vztahu mezi rozměry a měřítkovými koeficienty jako výše dostaneme rovnici 3d=42d=42d=34d=3. To znamená, že rozměr Kochovy sněhové vločky je d=log34≈1,262. To znamená, že rozměr Kochovy sněhové vločky je d=log34≈1,262.
Plocha
Tvorba Kochovy sněhové vločky je téměř jako rekurzivní posloupnost: známe výchozí tvar (trojúhelník) a víme, jak se dostat od jednoho členu k dalšímu (přidáním dalších trojúhelníků na každou hranu):


nové trojúhelníky

nové trojúhelníky

nové trojúhelníky
Po první iteraci se počet nově přidaných trojúhelníků v každém kroku zvětšuje. Současně se plocha těchto nových trojúhelníků v každém kroku zmenšuje o faktor
Řekněme, že první trojúhelník má plochu 1. Pak celková plocha dalších tří trojúhelníků je 3×19=13. To znamená, že v každém kroku se plocha těchto nových trojúhelníků zmenšuje. Všechny následující kroky tvoří geometrickou řaduaritmetickou řadukvadratickou řadu se společným poměrem 499443.
Pomocí vzorce pro součet nekonečných geometrických řad můžeme vypočítat, že celková plocha Kochovy sněhové vločky je
A=1+13×11-491+949-14=85=1.
.6.
Obvod
Můžeme se také pokusit vypočítat obvod Kochovy sněhové vločky. Jak jsme již viděli dříve, délka obvodu se při každém kroku mění o faktor 433414.
To znamená, že opět máme geometrickou řadu – v tomto případě však nekonvergujekonverguje k 0nemá první člen. To znamená, že obvod Kochovy sněhové vločky je ve skutečnosti nekonečně dlouhý!

Pokud se vám to zdá neintuitivní, stačí si uvědomit, že v každém kroku násobíme obvod číslem 43, a to nekonečně mnohokrát.
Je téměř nemyslitelné, že můžete mít útvar s konečným povrchem a zároveň nekonečným obvodem – ale to je jen jedna z mnoha nečekaných vlastností fraktálů.
Vymyslíte nějaké další způsoby, jak vytvořit vlastní fraktály?
„Moje duše se spirálovitě točí po zmrzlých fraktálech všude kolem…“
Mengerova houba
Fraktály nemusí být „ploché“, jako mnohé z výše uvedených příkladů. Jedním z nejznámějších fraktálů, které vypadají trojrozměrně, je Mengerova houba, pojmenovaná po matematikovi Karlu Mengerovi, který ji poprvé popsal v roce 1926.
Začneme s pevnou krychlí a do jejích stěn opakovaně vrtáme menší a menší otvory. Každá nová iterace otvorů má 131214 šířky předchozí iterace otvorů.
Krychle 3×3×3 se skládá z 27 menších krychlí, zde jsme však některé z nich odstranili. Mengerova houba se skládá z kopií sebe sama, které jsou 3x menší.
Nyní se můžeme pokusit vypočítat rozměr d Mengerovy houby stejně jako výše u Kochovy sněhové vločky. V tomto případě dostaneme 3d=20, neboli d=log320≈2,727.
Pokud si představíme, že bychom vyřezávali další a další díry, a to nekonečně mnohokrát, nezbyl by nám žádný skutečný objem. Proto je krychle „ne zcela“ trojrozměrná!
Fraktálové pobřeží
Jednou z klíčových vlastností všech fraktálů, které jsme dosud viděli, je, že je můžete „přibližovat“ donekonečna a vždy najdete nové vzory. Kolem roku 1920 si britský matematik Lewis Fry Richardson uvědomil, že totéž platí pro hranice nebo pobřeží mnoha zemí.
Začínáte se základním tvarem země a při zvětšování přidáváte říční zátoky, zálivy a ústí řek, pak jednotlivé útesy, skály, oblázky atd:
Toto je značný problém, když se snažíte vypočítat délku hranice země – jak se rozhodnete, jak daleko přiblížit a která zákoutí zahrnout?
Jedním ze způsobů, jak změřit délku pobřeží Velké Británie, je například vzít dlouhé pravítko, obejít všechny její pláže a pak sečíst všechny vzdálenosti.
Je-li pravítko dlouhé ${pravítek}km, musíme ho použít ${počet}krát, takže dostaneme celkovou délku pobřeží ${počet}km. × ${pravítek} = ${počet * pravítek}km.
Můžeme prostě pokračovat dál, s menšími a menšími pravítky, a pokaždé by se náš výsledek délky pobřeží o něco prodloužil. Stejně jako u předchozí Kochovy sněhové vločky se zdá, že pobřeží Británie je nekonečně dlouhé! Tomuto jevu se často říká paradox pobřeží.
O několik desetiletí později narazil matematik Benoit Mandelbrot na Richardsonovu práci ve vyřazené knize z knihovny, když pracoval v IBM. Uvědomil si její význam a také to, jak souvisí s novějším výzkumem fraktálů a dimenzí.
Břehová čára Británie jistě „vypadá“ fraktálně, ale není soběpodobná, jako jiné fraktály, které jsme viděli dříve. Abychom zjistili jeho velikost, můžeme ho nakreslit do mřížky a spočítat počet políček, se kterými se protíná.
Zpočátku se v něm protíná 88 políček. Pokud měřítko pobřeží zvětšíme na dvojnásobek, bude se protínat 197 buněk – tedy více než dvakrát tolik!
Velikost pobřežní čáry se zvětšila o faktor 19788. Stejně jako dříve to znamená, že rozměr pobřeží je
d=log219788≈1,16
Pokud bychom to zopakovali s většími mřížkami, zjistili bychom, že rozměr pobřeží Velké Británie je ve skutečnosti přibližně 1,21. To znamená, že rozměr pobřeží je větší než rozměr mřížky. Mandelbrot si uvědomil, že tento fraktální rozměr je také mírou drsnosti tvaru – nový koncept, pro který našel důležité využití v mnoha dalších oblastech matematiky a vědy.
Další fraktály v přírodě a technice
Přestože se skutečné fraktály v přírodě nikdy nemohou objevit, existuje mnoho objektů, které vypadají téměř jako fraktály. Rostliny, sněhové vločky a pobřežní linie jsme již viděli a zde je několik dalších příkladů:
Pohoří ve střední Asii
Delta řeky Gangy v Indii
Blesky
. Cévy v sítnici
Grand Canyon v USA
Mraky
Všechny tyto objekty se mohou jevit jako zcela náhodné, ale stejně jako u fraktálů existuje základní vzorec, který určuje jejich vznik. Matematika nám může pomoci tyto tvary lépe pochopit a fraktály mají využití v oborech, jako je medicína, biologie, geologie a meteorologie.
Počítačem generovaný fraktální terén
Fraktály můžeme také použít k vytvoření realistických „kopií“ přírody, například jako krajiny a textury používané ve videohrách nebo počítačem generovaných filmech. Voda, hory a mraky na tomto obrázku jsou zcela vytvořeny počítačem pomocí fraktálů!
A tento proces můžeme dokonce obrátit a komprimovat digitální obrázky, abychom zmenšili velikost jejich souborů. První algoritmy vyvinuli Michael Barnsley a Alan Sloan v 80. letech 20. století a nové se zkoumají dodnes.
.