En observant la nature, vous avez peut-être remarqué des plantes complexes comme celles-ci :


Cette fougère est constituée de nombreuses petites feuilles qui se ramifient à partir d’une plus grande.


Ce brocoli Romanesco est constitué de petites conescubessphères s’enroulant en spirale autour d’une plus grande.
Au départ, ces formes semblent très complexes – mais en y regardant de plus près, on peut remarquer qu’elles suivent toutes deux un modèle relativement simple : toutes les parties individuelles des plantes ont exactement la même apparence que la plante entière, juste plus petite. Le même schéma se répète encore et encore, à des échelles plus petites.
En mathématiques, on appelle cette propriété l’auto-similarité, et les formes qui la possèdent sont appelées fractales. Elles font partie des objets les plus beaux et les plus bizarres de toutes les mathématiques.
Pour créer nos propres fractales, nous devons commencer par un motif simple et le répéter encore et encore, à des échelles plus petites.
Un des motifs les plus simples pourrait être un segment de ligne, avec deux autres segments se ramifiant à une extrémité. Si nous répétons ce motif, ces deux segments bleus auront également deux autres branches à leurs extrémités.
Vous pouvez déplacer les points bleus pour modifier la longueur et l’angle de toutes les branches. Puis augmentez le nombre d’itérations en utilisant le curseur ci-dessous.
Selon la position des branches, vous pouvez faire des motifs complètement différents – ressemblant à la fougère ci-dessus, à un arbre, ou à des pentagones imbriqués. Que pouvez-vous trouver d’autre ?
Une autre fractale célèbre est le triangle de Sierpinski. Dans ce cas, nous commençons par un grand triangle équilatéral, puis nous découpons à plusieurs reprises des triangles plus petits dans les parties restantes.
Remarquez comment la forme finale est constituée de trois copies identiques d’elle-même, et chacune d’entre elles est constituée de copies encore plus petites du triangle entier ! Vous pourriez continuer à zoomer sur le triangle pour toujours, et les motifs et les formes continueront toujours à se répéter.
Les plantes au début de ce chapitre ressemblent à des fractales, mais il est clairement impossible de créer de véritables fractales dans la vie réelle. Si nous répétons sans cesse le même motif, de plus en plus petit, nous finirions par arriver à des cellules, des molécules ou des atomes qui ne peuvent plus être divisés.
Cependant, en utilisant les mathématiques, nous pouvons réfléchir aux propriétés que les vraies fractales « auraient » – et celles-ci sont très surprenantes…
Dimensions des fractales
Premièrement, réfléchissons à la dimension des fractales. Une ligne a une dimension . En la mettant à l’échelle par un facteur 2, sa longueur augmente d’un facteur 21=2. Évidemment!
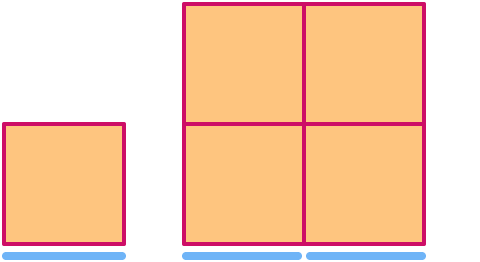
Un carré a pour dimension . Lorsqu’on le met à l’échelle par un facteur 2, sa surface augmente par un facteur 22= .
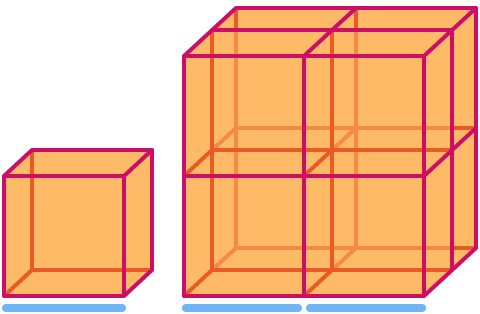
Un cube a pour dimension . En le mettant à l’échelle par un facteur 2, son volume augmente par un facteur 23= . Remarquez que le plus grand cube de l’image est constitué de 8 copies du plus petit !
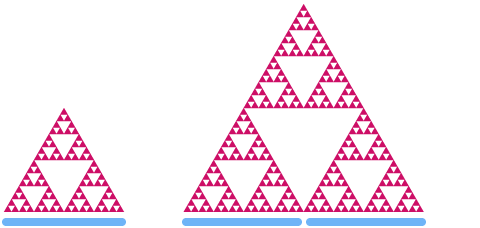
Regardons maintenant le triangle de Sierpinski. Si nous le mettons à l’échelle par un facteur 2, vous pouvez voir que sa « surface » augmente par un facteur de .
Disons que d est la dimension du triangle de Sierpinski. En utilisant le même schéma que ci-dessus, nous obtenons 2d=3. En d’autres termes, d = log23log32 ≈ 1,585…
Mais attendez… comment quelque chose peut-il avoir une dimension qui n’est pas un nombre entier ? Cela semble impossible, mais ce n’est qu’une des propriétés étranges des fractales. En fait, c’est ce qui donne aux fractales leur nom : elles ont une dimension fractionnaire.
A chaque itération, nous enlevons une partie de l’aire du triangle de Sierpinski. Si nous pouvions faire cela une infinité de fois, il ne resterait en fait aucune aire : c’est pourquoi le triangle de Sierpinski est quelque chose entre une aire bidimensionnelle, et une ligne unidimensionnelle.
Bien que de nombreuses fractales soient auto-similaires, une meilleure définition est que les fractales sont des formes qui ont une dimension non-entière.
Le flocon de Koch
Il y a beaucoup de formes dans la nature qui ressemblent à des fractales. Nous avons déjà vu quelques plantes au début de ce chapitre. D’autres grands exemples sont les flocons de neige et les cristaux de glace :
Pour créer notre propre flocon de neige fractal, nous devons une fois de plus trouver une procédure simple que nous pouvons appliquer encore et encore.
Comme pour le triangle de Sierpinski, commençons par un seul triangle équilatéral. Cependant, plutôt que de supprimer des triangles plus petits à chaque étape, nous ajoutons des triangles plus petits le long du bord. La longueur de côté de chaque triangle est égale à 131412 des triangles de l’étape précédente.
La forme résultante est appelée le flocon de neige de Koch, du nom du mathématicien suédois Helge von Koch. Remarquez, une fois de plus, que les petites sections du bord du flocon de neige ont exactement la même apparence que les sections plus grandes.
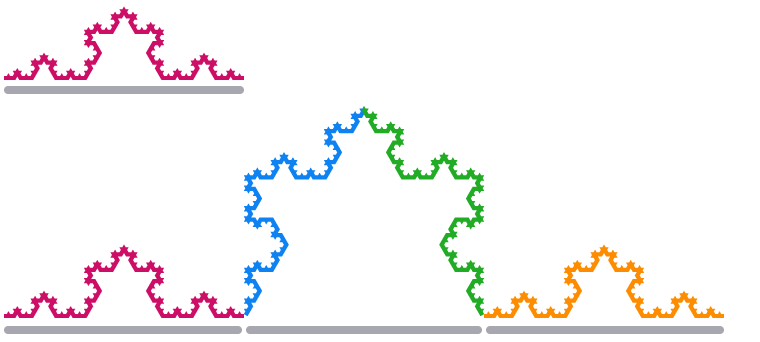
Lorsque nous mettons à l’échelle un segment de bord du flocon de neige de Koch par un facteur 3, sa longueur quadruplestripledouble.
En utilisant la même relation entre les dimensions et les facteurs d’échelle que ci-dessus, nous obtenons l’équation 3d=42d=42d=34d=3. Cela signifie que la dimension du flocon de neige de Koch est d=log34≈1,262.
Aire
Créer les flocons de neige de Koch, c’est presque comme une séquence récursive : on connaît la forme de départ (un triangle), et on sait comment passer d’un terme à l’autre (en ajoutant d’autres triangles sur chaque bord) :


nouveaux triangles

nouveaux triangles

nouveaux triangles
Après la première itération, le nombre de nouveaux triangles ajoutés augmente d’un facteur de à chaque étape. En même temps, l’aire de ces nouveaux triangles diminue d’un facteur de à chaque étape.
Disons que le premier triangle a une aire de 1. Alors l’aire totale des trois triangles suivants est 3×19=13. Les étapes suivantes forment toutes une série géométriqueune série arithmétiqueune série quadratique, avec un rapport commun 499443.
En utilisant la formule de la somme des séries géométriques infinies, nous pouvons calculer que l’aire totale du flocon de neige de Koch est
A=1+13×11-491+949-14=85=1.6.
Périmètre
Nous pouvons également essayer de calculer le périmètre du flocon de neige de Koch. Comme nous l’avons déjà vu précédemment, la longueur du périmètre change par un facteur de 433414 à chaque étape.
Cela signifie que, une fois de plus, nous avons une série géométrique – mais dans ce cas, elle ne converge pasconverge vers 0n’a pas de premier terme. Cela signifie que le périmètre du flocon de neige de Koch est en fait infiniment long !

Si cela semble contre-intuitif, il suffit de se rappeler que nous multiplions le périmètre par 43 à chaque étape, et nous le faisons infiniment de fois.
Il est presque impensable que vous puissiez avoir une forme avec une surface finie et aussi une circonférence infinie – mais ce n’est qu’une des nombreuses propriétés inattendues des fractales.
Pouvez-vous imaginer d’autres façons de créer vos propres fractales ?
« Mon âme est en spirale sur des fractales gelées tout autour… »
Menger Sponge
Les fractales n’ont pas besoin d’être « plates », comme beaucoup des exemples ci-dessus. L’une des fractales les plus célèbres qui ont l’air tridimensionnelles est l’éponge de Menger, nommée d’après le mathématicien Karl Menger qui l’a décrite pour la première fois en 1926.
Nous commençons par un cube solide, et nous perçons de façon répétée des trous de plus en plus petits dans ses côtés. Chaque nouvelle itération de trous a 131214 la largeur de l’itération précédente de trous.
Un cube 3×3×3 est constitué de 27 cubes plus petits, mais ici nous en avons retiré certains. L’éponge de Menger est constituée de copies d’elle-même, qui sont 3 fois plus petites.
Maintenant nous pouvons essayer de calculer la dimension d de l’éponge de Menger comme nous l’avons fait pour le flocon de neige de Koch ci-dessus. Dans ce cas, nous obtenons 3d=20, ou d=log320≈2,727.
Si vous imaginez découper de plus en plus de trous, une infinité de fois, il ne resterait aucun volume réel. C’est pourquoi le cube n’est « pas tout à fait » tridimensionnel !
Lignes côtières fractales
L’une des principales caractéristiques de toutes les fractales que nous avons vues jusqu’à présent est que vous pouvez « zoomer » à l’infini et toujours trouver de nouveaux motifs. Vers 1920, le mathématicien britannique Lewis Fry Richardson a réalisé qu’il en était de même pour la frontière ou le littoral de nombreux pays.
On commence par la forme de base du pays et, en zoomant, on ajoute les bras de rivière, les baies et les estuaires, puis les falaises individuelles, les rochers, les galets, et ainsi de suite :
C’est un problème important quand on essaie de calculer la longueur de la frontière d’un pays – comment décider jusqu’où zoomer, et quels coins et recoins inclure ?
Une façon de mesurer la longueur du littoral de la Grande-Bretagne, par exemple, est de prendre une longue règle, de faire le tour de ses plages, puis d’additionner toutes les distances.
Si la règle fait ${rulers}km, nous devons l’utiliser ${count} fois, et nous obtenons donc un littoral total de ${count}. × ${rulers} = ${count * rulers}km.
Nous pouvons simplement continuer, avec des règles de plus en plus petites, et à chaque fois notre résultat pour la longueur du littoral serait un peu plus long. Tout comme le flocon de neige de Koch auparavant, il semble que le littoral de la Grande-Bretagne soit infiniment long ! Ce phénomène est souvent appelé le paradoxe du littoral.
Quelques décennies plus tard, le mathématicien Benoit Mandelbrot tomba sur le travail de Richardson dans un livre de bibliothèque mis au rebut, alors qu’il travaillait chez IBM. Il a reconnu son importance, et aussi comment il est lié à des recherches plus récentes sur les fractales et les dimensions.
Le littoral de la Grande-Bretagne « ressemble » certainement à une fractale, mais il n’est pas auto-similaire, comme d’autres fractales que nous avons vues auparavant. Afin de trouver sa taille, nous pouvons le dessiner sur une grille et compter le nombre de cellules avec lesquelles il se croise.
Au départ, il y a 88 cellules qui se croisent. Si nous mettons le littoral à l’échelle par un facteur 2, il y a 197 cellules qui s’intersectent – plus du double !
La dimension du trait de côte a augmenté d’un facteur 19788. Comme précédemment, cela signifie que la dimension du littoral est
d=log219788≈1,16
Si nous répétons cela avec des grilles plus grandes, nous trouverions que la dimension du littoral britannique est en fait d’environ 1,21. Mandelbrot a réalisé que cette dimension fractale est également une mesure de la rugosité d’une forme – un nouveau concept, pour lequel il a trouvé des applications importantes dans de nombreux autres domaines des mathématiques et des sciences.
Plus de fractales dans la nature et la technologie
Bien que les vraies fractales ne puissent jamais apparaître dans la nature, il existe de nombreux objets qui ressemblent presque à des fractales. Nous avons déjà vu des plantes, des flocons de neige et des lignes de côte, et voici d’autres exemples :
Chaîne de montagnes en Asie centrale
Delta du Gange en Inde
Éclairs
. Vaisseaux sanguins dans la rétine
Grand Canyon aux USA
Nuages
Tous ces objets peuvent sembler complètement aléatoires, mais, tout comme les fractales, il existe un modèle sous-jacent qui détermine la façon dont ils sont formés. Les mathématiques peuvent nous aider à mieux comprendre ces formes, et les fractales ont des applications dans des domaines comme la médecine, la biologie, la géologie et la météorologie.
Terrain fractal généré par ordinateur
Nous pouvons également utiliser les fractales pour créer des « copies » réalistes de la nature, par exemple sous forme de paysages et de textures utilisés dans les jeux vidéo ou les films générés par ordinateur. L’eau, les montagnes et les nuages de cette image sont entièrement réalisés par un ordinateur, à l’aide de fractales !
Et nous pouvons même inverser ce processus pour compresser les images numériques, afin de réduire leur taille de fichier. Les premiers algorithmes ont été développés par Michael Barnsley et Alan Sloan dans les années 1980, et de nouveaux algorithmes font encore l’objet de recherches aujourd’hui.