Katsellessasi luontoa olet ehkä huomannut tällaisia monimutkaisia kasveja:


Tämä saniainen koostuu monista pienistä lehdistä, jotka haarautuvat suuremmasta lehdestä.


Tämä roomalaisparsakaali (Romanesco-parsakaali) koostuu pienemmistä, spiraalimaisesti isomman ympärillä kiertyvistä kartiopalloista.
Aluksi nämä näyttävät erittäin monimutkaisilta muodoilta – mutta kun katsot tarkemmin, saatat huomata, että molemmat noudattavat suhteellisen yksinkertaista kaavaa: kaikki yksittäiset osat näyttävät täsmälleen samalta kuin koko kasvi, vain pienemmiltä. Sama kuvio toistuu yhä uudelleen ja uudelleen pienemmissä mittakaavoissa.
Matematiikassa kutsumme tätä ominaisuutta itsesimilaarisuudeksi, ja muotoja, joissa sitä esiintyy, kutsutaan fraktaaleiksi. Ne ovat eräitä koko matematiikan kauneimpia ja omituisimpia kohteita.
Luodaksemme omia fraktaalejamme meidän on aloitettava yksinkertaisesta kuviosta ja toistettava sitä yhä uudelleen ja uudelleen pienemmissä mittakaavoissa.
Yksi yksinkertaisimmista kuvioista voisi olla viivasegmentti, jonka toisesta päästä haarautuu kaksi muuta segmenttiä. Jos toistamme tämän kuvion, myös näiden molempien sinisten segmenttien päihin tulee kaksi muuta haaraa.
Voit siirtää sinisiä pisteitä muuttaaksesi kaikkien haarojen pituutta ja kulmaa. Lisää sitten iteraatioiden määrää alla olevalla liukusäätimellä.
Oksien sijainnista riippuen voit tehdä täysin erilaisia kuvioita – yllä olevan saniaisen, puun tai sisäkkäisten viisikulmioiden näköisiä. Mitä muuta voit löytää?
Toinen kuuluisa fraktaali on Sierpinskin kolmio. Tässä tapauksessa aloitetaan suuresta, tasasivuisesta kolmiosta ja leikataan sitten jäljelle jäävistä osista toistuvasti pienempiä kolmioita.
Huomaa, kuinka lopullinen muoto koostuu kolmesta identtisestä kopiosta itsestään, ja jokainen näistä koostuu vielä pienemmistä kopioista koko kolmiosta! Voit jatkaa kolmion zoomaamista loputtomiin, ja kuviot ja muodot toistuvat aina uudelleen.
Tämän luvun alussa esitetyt kasvit näyttävät aivan fraktaaleilta, mutta todellisten fraktaalien luominen tosielämässä on selvästi mahdotonta. Jos toistaisimme samaa kuviota yhä uudestaan ja uudestaan, yhä pienempiä ja pienempiä, pääsisimme lopulta soluihin, molekyyleihin tai atomeihin, joita ei voi enää jakaa.
Matematiikan avulla voimme kuitenkin miettiä ominaisuuksia, joita todellisilla fraktaaleilla ”olisi” – ja ne ovat hyvin yllättäviä…
Fraktaalien dimensiot
Mietitäänpä ensin fraktaalien dimensioita. Viivalla on ulottuvuus . Kun sitä skaalataan kertoimella 2, sen pituus kasvaa kertoimella 21=2. Ilmeisesti!
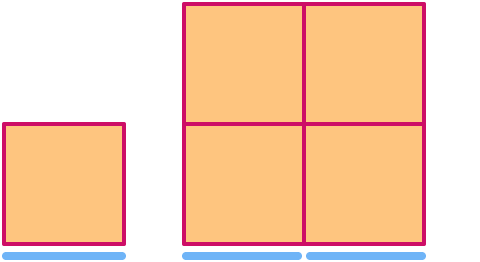
Neliöllä on ulottuvuus . Kun sitä skaalataan kertoimella 2, sen pinta-ala kasvaa kertoimella 22= .
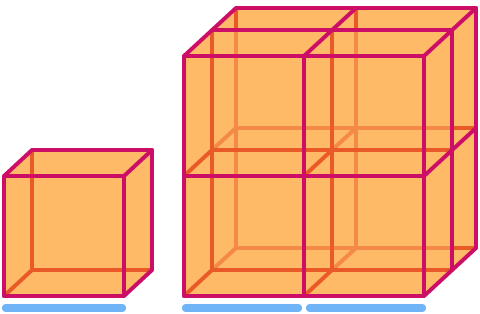
Kuutiolla on ulottuvuus . Kun sitä skaalataan kertoimella 2, sen tilavuus kasvaa kertoimella 23= . Huomaa, että kuvan suurempi kuutio koostuu 8 kopiosta pienemmästä!
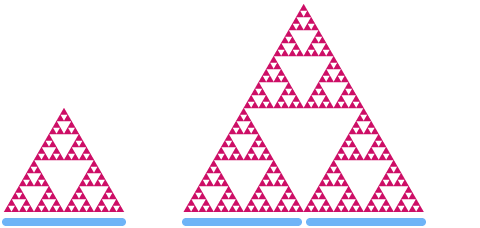
Katsotaan nyt Sierpinskin kolmio. Jos skaalaamme sen kertoimella 2, näet, että sen ”pinta-ala” kasvaa kertoimella.
Sanotaan, että d on Sierpinski-kolmion ulottuvuus. Käyttämällä samaa kaavaa kuin edellä, saadaan 2d=3. Toisin sanoen d = log23log32 ≈ 1.585…
Mutta hetkinen … miten jollakin voi olla ulottuvuus, joka ei ole kokonaisluku? Se tuntuu mahdottomalta, mutta tämä on vain yksi fraktaalien oudoista ominaisuuksista. Itse asiassa juuri tämä antaa fraktaaleille niiden nimen: niillä on murto-ulottuvuus.
Joka iteraatiolla poistamme osan Sierpinski-kolmion pinta-alasta. Jos voisimme tehdä tämän äärettömän monta kertaa, mitään pinta-alaa ei itse asiassa jäisi jäljelle: siksi Sierpinskin kolmio on jotakin kaksiulotteisen alueen ja yksiulotteisen viivan väliltä.
Vaikka monet fraktaalit ovat itsesimilaarisia, parempi määritelmä on, että fraktaalit ovat muotoja, joilla on epäkokonaisulotteinen ulottuvuus.
Kochin lumihiutale
Luonnossa on monia fraktaalien kaltaisia muotoja. Olemme jo nähneet joitakin kasveja tämän luvun alussa. Muita hyviä esimerkkejä ovat lumihiutaleet ja jääkiteet:
Luodaksemme oman fraktaalisen lumihiutaleen, meidän on jälleen kerran löydettävä yksinkertainen menettelytapa, jota voimme soveltaa yhä uudelleen.
Aloitetaan Sierpinski-kolmion tapaan yhdestä, tasasivuisesta kolmiosta. Sen sijaan, että poistaisimme pienempiä kolmioita jokaisella askeleella, lisäämme kuitenkin pienempiä kolmioita reunaa pitkin. Jokaisen kolmion sivun pituus on 131412 edellisen askeleen kolmioista.
Tuloksena olevaa muotoa kutsutaan Kochin lumihiutaleeksi, joka on nimetty ruotsalaisen matemaatikon Helge von Kochin mukaan. Huomaa jälleen kerran, että lumihiutaleen pienet reunaosuudet näyttävät täsmälleen samalta kuin suuremmat osuudet.
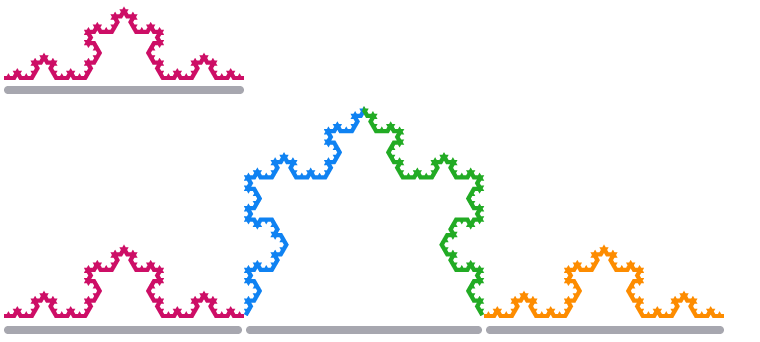
Kun skaalaamme Kochin lumihiutaleen yhden reunaosuuden kolminkertaiseksi, sen pituus nelinkertaistuu.
Käyttämällä samaa mittojen ja mittakertoimien välistä suhdetta kuin edellä, saadaan yhtälö 3d=42d=42d=34d=3. Tämä tarkoittaa, että Kochin lumihiutaleen ulottuvuus on d=log34≈1,262.
Pinta-ala
Kochin lumihiutaleiden luominen on melkein kuin rekursiivinen sarja: tiedämme lähtömuodon (kolmio) ja tiedämme, miten pääsemme termistä seuraavaan (lisäämällä jokaiseen reunaan lisää kolmioita):


uudet kolmiot

uudet kolmiot

uudet kolmiot
Ensimmäisen iteraatiokierroksen jälkeen lisättyjen uusien kolmioiden määrä lisääntyy jokaisella askeleella. Samalla näiden uusien kolmioiden pinta-ala pienenee jokaisella askeleella kertoimella
Oletetaan, että ensimmäisen kolmion pinta-ala on 1. Silloin kolmen seuraavan kolmion kokonaispinta-ala on 3×19=13. Seuraavat askeleet muodostavat kaikki geometrisen sarjanaritmeettinen sarjaquadratinen sarja, jonka yhteinen suhdeluku on 499443.
Käyttämällä äärettömien geometristen sarjojen summan kaavaa voimme laskea, että Kochin lumihiutaleen kokonaispinta-ala on
A=1+13×11-491+949-14=85=1.6.
Piiri
Voidaan myös yrittää laskea Kochin lumihiutaleen kehä. Kuten olemme jo aiemmin nähneet, kehän pituus muuttuu jokaisella askeleella kertoimella 433414.
Tämä tarkoittaa, että meillä on jälleen kerran geometrinen sarja – mutta tässä tapauksessa se ei konvergoiKonvergenssi on 0Ei ole ensimmäistä termiä. Tämä tarkoittaa, että Kochin lumihiutaleen ympärysmitta on itse asiassa äärettömän pitkä!

Jos tämä tuntuu vastenmieliseltä, muista vain, että kerromme ympärysmitan 43:lla jokaisella askeleella, ja teemme tämän äärettömän monta kertaa.
On melkein käsittämätöntä, että voi olla muoto, jolla on äärellinen pinta-ala ja myös ääretön ympärysmitta – mutta tämä on vain yksi fraktaalien monista odottamattomista ominaisuuksista.
Keksitkö muita tapoja luoda omia fraktaaleja?
”Sieluni pyörii spiraalimaisesti jäätyneillä fraktaaleilla ympäriinsä…”
Menger Sponge
Fraktaalien ei tarvitse olla ”litteitä”, kuten monet yllä olevista esimerkeistä. Yksi tunnetuimmista kolmiulotteisen näköisistä fraktaaleista on Mengerin sieni, joka on saanut nimensä matemaatikko Karl Mengerin mukaan, joka kuvasi sen ensimmäisen kerran vuonna 1926.
Aloitetaan kiinteästä kuutiosta ja porataan sen sivuihin toistuvasti yhä pienempiä reikiä. Jokaisen uuden reikäkierroksen leveys on 131214 edellisen reikäkierroksen leveyttä.
3×3×3-kuutio koostuu 27 pienemmästä kuutiosta, mutta tässä olemme poistaneet niistä osan. Mengerin sieni koostuu itsensä kopioista, jotka ovat 3 kertaa pienempiä.
Nyt voimme yrittää laskea Mengerin sienen ulottuvuuden d aivan kuten teimme edellä Kochin lumihiutaleelle. Tällöin saamme 3d=20 eli d=log320≈2.727.
Jos kuvitellaan leikkaavamme yhä enemmän ja enemmän reikiä, äärettömän monta kertaa, varsinaista tilavuutta ei jäisi jäljelle. Siksi kuutio ei ole ”aivan” kolmiulotteinen!
Fraktaaliset rantaviivat
Yksi kaikkien tähän mennessä näkemiemme fraktaalien tärkeimmistä ominaisuuksista on se, että niitä voi ”zoomata” loputtomiin ja löytää aina uusia kuvioita. Noin vuonna 1920 brittiläinen matemaatikko Lewis Fry Richardson tajusi, että sama pätee myös monien maiden rajoihin tai rannikkolinjoihin.
Aloitetaan maan perusmuodosta, ja kun zoomataan lähemmäs, lisätään jokisuita, lahtia ja suistoja, sitten yksittäisiä kallioita, kallioita, kiviä ja niin edelleen:
Tämä on merkittävä ongelma, kun yritetään laskea maan rajan pituutta – miten päätetään, kuinka pitkälle zoomataan ja mitkä nurkat ja kolkat otetaan mukaan?
Yksi tapa mitata esimerkiksi Britannian rantaviivan pituus on ottaa pitkä viivoitin, kävellä sen rannat ympäri ja laskea sitten kaikki etäisyydet yhteen.
Jos viivoitin on ${viivoitin}km pitkä, joudumme käyttämään sitä ${lukua} kertaa, joten saamme kokonaisrannikkoviivaksi ${lukua}m. × ${rulers} = ${count * rulers}km.
Voimme vain jatkaa tätä yhä pienemmillä ja pienemmillä viivottimilla, ja joka kerta tuloksemme rantaviivan pituudesta tulisi hieman pidempi. Aivan kuten Kochin lumihiutale aiemmin, näyttää siltä, että Britannian rantaviiva on äärettömän pitkä! Tätä kutsutaan usein rantaviivan paradoksiksi.
Muutamaa vuosikymmentä myöhemmin matemaatikko Benoit Mandelbrot törmäsi Richardsonin työhön hylätyssä kirjastokirjassa työskennellessään IBM:llä. Hän tunnisti sen merkityksen ja myös sen yhteyden uudempaan tutkimukseen fraktaaleista ja ulottuvuuksista.
Britannian rantaviiva ”näyttää” toki fraktaalilta, mutta se ei ole itsesimilaarinen, kuten muut aiemmin näkemämme fraktaalit. Löytääksemme sen koon voimme piirtää sen ruudukkoon ja laskea niiden solujen lukumäärän, joiden kanssa se risteää.
Aluksi risteäviä soluja on 88. Jos skaalaamme rantaviivan kertoimella 2, risteäviä soluja on 197 – yli kaksinkertainen määrä!
Rantaviivan koko on kasvanut kertoimella 19788. Kuten aiemminkin, tämä tarkoittaa, että rantaviivan ulottuvuus on
d=log219788≈1.16
Jos toistaisimme tämän suuremmilla ruuduilla, huomaisimme, että Britannian rantaviivan ulottuvuus on itse asiassa noin 1.21. Mandelbrot tajusi, että tämä fraktaaliulottuvuus on myös muodon karheuden mitta – uusi käsite, jolle hän löysi tärkeitä sovelluksia monilla muilla matematiikan ja luonnontieteiden aloilla.
Muuta fraktaaleja luonnossa ja teknologiassa
Vaikka todellisia fraktaaleja ei voi koskaan esiintyä luonnossa, on olemassa monia kohteita, jotka näyttävät melkein fraktaaleilta. Olemme jo nähneet kasveja, lumihiutaleita ja rantaviivoja, ja tässä on lisää esimerkkejä:
Vuoristo Keski-Aasiassa
Ganges-joen suisto Intiassa
Salamoita
Verisuonet verkkokalvolla
Grand Canyon Yhdysvalloissa
Pilvet
Kaikki nämä kohteet saattavat vaikuttaa täysin satunnaisilta, mutta fraktaalien tapaan niiden taustalla on kuvio, joka määrää, miten ne muodostuvat. Matematiikka voi auttaa meitä ymmärtämään muotoja paremmin, ja fraktaaleilla on sovelluksia esimerkiksi lääketieteen, biologian, geologian ja meteorologian aloilla.
Tietokoneella luodut fraktaalimaastot
Fraktaalien avulla voimme myös luoda realistisia ”kopioita” luonnosta, esimerkiksi videopeleissä tai tietokoneella luoduissa elokuvissa käytettävinä maisemina ja tekstuureina. Tämän kuvan vesi, vuoret ja pilvet on tehty kokonaan tietokoneella fraktaalien avulla!
Ja voimme jopa kääntää tämän prosessin päinvastaiseksi digitaalisten kuvien pakkaamiseksi, jotta niiden tiedostokoko pienenee. Ensimmäiset algoritmit kehittelivät Michael Barnsley ja Alan Sloan 1980-luvulla, ja uusia algoritmeja tutkitaan edelleen.