Når du ser dig omkring i naturen, har du måske bemærket indviklede planter som disse:


Denne bregne består af mange små blade, der forgrener sig fra et større.


Denne romanesco-broccoli består af mindre kegleformede kuglesfærer, der spiralerer rundt om et større.
Umiddelbart ser det ud til at være meget komplekse former – men når man ser nærmere efter, vil man måske bemærke, at de begge følger et relativt simpelt mønster: Alle de enkelte plantedele ser nøjagtig ens ud som hele planten, bare mindre. Det samme mønster gentages igen og igen, i mindre skalaer.
I matematikken kalder vi denne egenskab for selv-similaritet, og former, der har den, kaldes fraktaler. De er nogle af de smukkeste og mest bizarre objekter i hele matematikken.
For at skabe vores egne fraktaler skal vi starte med et simpelt mønster og derefter gentage det igen og igen i mindre skalaer.
Et af de enkleste mønstre kan være et linjestykke, hvorfra der forgrener sig yderligere to segmenter i den ene ende. Hvis vi gentager dette mønster, vil begge disse blå segmenter også have yderligere to grene i deres ender.
Du kan flytte de blå prikker for at ændre længden og vinklen på alle grenene. Øg derefter antallet af gentagelser ved hjælp af skyderen nedenfor.
Afhængigt af grenenes placering kan du lave helt forskellige mønstre – de kan se ud som bregnen ovenfor, et træ eller indlejrede femkanter. Hvad kan du ellers finde?
En anden berømt fraktal er Sierpinski-trekanten. I dette tilfælde starter vi med en stor, ligesidet trekant og skærer derefter gentagne gange mindre trekanter ud af de resterende dele.
Bemærk, hvordan den endelige form består af tre identiske kopier af sig selv, og hver af disse består af endnu mindre kopier af hele trekanten! Du kan blive ved med at zoome ind i trekanten i al evighed, og mønstrene og formerne vil altid blive ved med at gentage sig.
Planterne i begyndelsen af dette kapitel ligner fraktaler, men det er tydeligvis umuligt at skabe ægte fraktaler i virkeligheden. Hvis vi bliver ved med at gentage det samme mønster igen og igen, mindre og mindre, ville vi til sidst nå frem til celler, molekyler eller atomer, som ikke længere kan deles.
Men ved hjælp af matematik kan vi tænke over de egenskaber, som ægte fraktaler “ville” have – og de er meget overraskende…
Fraktale dimensioner
Først skal vi tænke over dimensionen af fraktaler. En linje har dimension . Når den skaleres med en faktor 2, øges dens længde med en faktor 21=2. Det er klart!
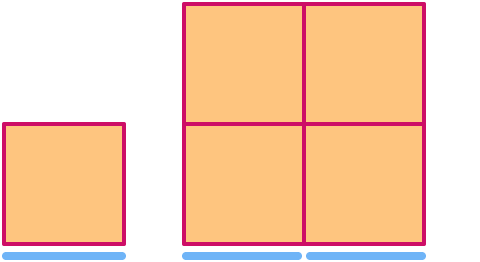
Et kvadrat har dimension . Når det skaleres med en faktor 2, øges dets areal med en faktor 22= .
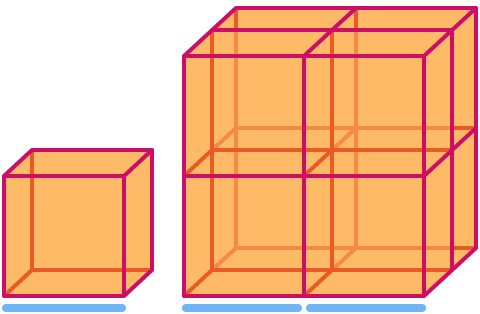
En terning har dimensionen . Når den skaleres med en faktor 2, øges dens rumfang med en faktor 23= . Bemærk, at den større terning på billedet består af 8 kopier af den mindre!
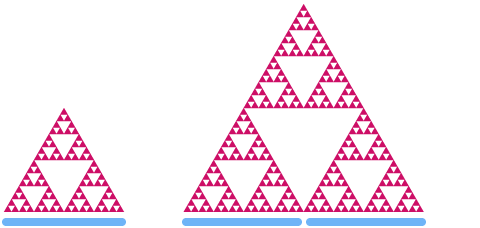
Nu skal vi se på Sierpinski-trekanten. Hvis vi skalerer den med en faktor 2, kan du se, at dens “areal” øges med en faktor på ,
Lad os sige, at d er dimensionen af Sierpinski trekanten. Ved at bruge det samme mønster som ovenfor får vi 2d=3. Med andre ord: d = log23log32 ≈ 1,585…
Men vent … hvordan kan noget have en dimension, der ikke er et heltal? Det virker umuligt, men det er bare en af fraktalernes mærkelige egenskaber. Det er faktisk det, der giver fraktaler deres navn: de har en brøkdimension.
Med hver iteration fjerner vi noget af arealet af Sierpinski-trekanten. Hvis vi kunne gøre dette uendeligt mange gange, ville der faktisk ikke være noget areal tilbage: det er derfor, Sierpinski-trekanten er noget mellem et todimensionelt areal og en endimensionel linje.
Som mange fraktaler er selvlignende, er en bedre definition, at fraktaler er former, der har en ikke-heltal dimension.
The Koch Snowflake
Der er mange former i naturen, der ligner fraktaler. Vi har allerede set nogle planter i begyndelsen af dette kapitel. Andre gode eksempler er snefnug og iskrystaller:
For at skabe vores eget fraktale snefnug skal vi endnu engang finde en simpel fremgangsmåde, som vi kan anvende igen og igen.
Lad os ligesom Sierpinski-trianglen starte med en enkelt, ligesidet trekant. Men i stedet for at fjerne mindre trekanter ved hvert trin tilføjer vi mindre trekanter langs kanten i stedet for at fjerne mindre trekanter. Sidelængden af hver trekant er 131412 af trekanterne i det foregående trin.
Den resulterende form kaldes Koch-snefnuget, opkaldt efter den svenske matematiker Helge von Koch. Bemærk endnu en gang, at små udsnit af snefnugets kant ser nøjagtig ens ud som større udsnit.
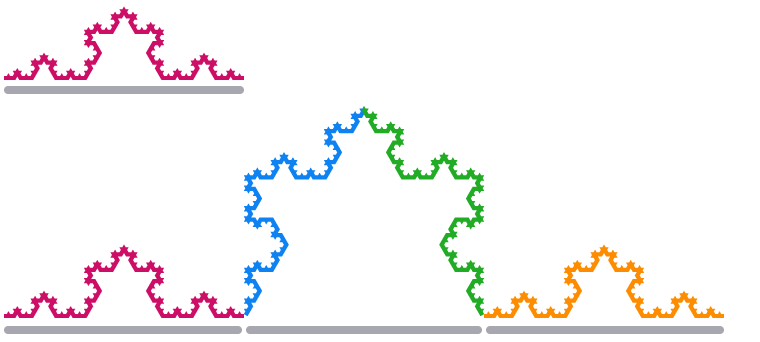
Når vi skalerer et kantudsnit af Koch-snefnuget med en faktor 3, bliver dets længde firedobbelt så lang som tre gange så lang.
Ved at bruge det samme forhold mellem dimensioner og skaleringsfaktorer som ovenfor får vi ligningen 3d=42d=42d=42d=34d=3. Det betyder, at dimensionen af Koch-snefnuget er d=log34≈1,262.
Areal
Skabelsen af Koch-snefnuget er næsten som en rekursiv sekvens: Vi kender startformen (en trekant), og vi ved, hvordan vi kommer fra et udtryk til det næste (ved at tilføje flere trekanter på hver kant):


nye trekanter

nye trekanter

nye trekanter
Efter den første iteration øges antallet af nye trekanter, der tilføjes, med en faktor på ved hvert trin. Samtidig falder arealet af disse nye trekanter med en faktor af ved hvert trin.
Lad os sige, at den første trekant har et areal på 1. Så er det samlede areal af de næste tre trekanter 3×19=13. De følgende trin danner alle en geometrisk seriearitmetisk seriekvadratisk serie, med fælles forhold 499443.
Ved hjælp af formlen for summen af uendelige geometriske serier kan vi udregne, at det samlede areal af Kochs snefnug er
A=1+13×11-491+949-14=85=1.6.
Perimeter
Vi kan også forsøge at beregne omkredsen af Koch-snefnuget. Som vi allerede har set før, ændrer længden af omkredsen sig med en faktor 433414 ved hvert trin.
Det betyder, at vi endnu en gang har en geometrisk serie – men i dette tilfælde konvergerer den ikkekonvergerer til 0har ikke en første term. Det betyder, at Kochs snefnugs omkreds faktisk er uendeligt lang!

Hvis dette virker kontraintuitivt, skal du blot huske, at vi multiplicerer omkredsen med 43 ved hvert trin, og det gør vi uendeligt mange gange.
Det er næsten utænkeligt, at man kan have en form med et endeligt areal og også en uendelig omkreds – men det er blot en af de mange uventede egenskaber ved fraktaler.
Kan du komme på andre måder at skabe dine egne fraktaler på?
“My soul is spiralling on frozen fractals all around…”
Menger Sponge
Fraktaler behøver ikke at være “flade”, som mange af eksemplerne ovenfor. Et af de mest berømte fraktaler, der ser tredimensionelle ud, er Menger-svampen, opkaldt efter matematikeren Karl Menger, der først beskrev den i 1926.
Vi starter med en massiv terning og borer gentagne gange mindre og mindre huller i dens sider. Hver ny gentagelse af huller har 131214 bredden af den foregående gentagelse af huller.
En 3×3×3×3 terning består af 27 mindre terninger, men her har vi fjernet nogle af disse. Menger-svampen består af kopier af sig selv, som er 3 gange mindre.
Nu kan vi forsøge at beregne dimensionen d af Menger-svampen ligesom vi gjorde for Koch-snefnuget ovenfor. I dette tilfælde får vi 3d=20, eller d=log320≈2,727.
Hvis man forestiller sig, at man skærer flere og flere huller ud, uendeligt mange gange, ville der ikke være noget egentligt volumen tilbage. Det er derfor, at terningen ikke er “helt” tredimensionel!
Fraktale kystlinjer
Et af de vigtigste kendetegn ved alle de fraktaler, vi har set indtil nu, er, at man kan “zoome ind” for evigt og altid finde nye mønstre. Omkring 1920 indså den britiske matematiker Lewis Fry Richardson, at det samme gælder for grænsen eller kystlinjen i mange lande.
Man starter med landets grundform, og efterhånden som man zoomer ind, tilføjer man flodindløb, bugter og flodmundinger, derefter individuelle klipper, klipper, klipper, småsten osv:
Dette er et væsentligt problem, når man forsøger at beregne længden af et lands grænser – hvordan beslutter man, hvor langt man skal zoome ind, og hvilke kroge og hjørner man skal medtage?
En måde, vi kunne måle længden af Storbritanniens kystlinje på, er f.eks. at tage en lang lineal, gå hele vejen rundt om landets strande og derefter lægge alle afstandene sammen.
Hvis linealen er ${rulers}km lang, skal vi bruge den ${count} gange, så vi får en samlet kystlinje på ${count}. × ${linealer} = ${count * linealer}km.
Vi kan bare blive ved, med mindre og mindre linealer, og hver gang vil vores resultat for kystlinjens længde blive en smule længere. Ligesom Kochs snefnug før, ser det ud til, at Storbritanniens kystlinje er uendeligt lang! Dette kaldes ofte for kystlinjeparadokset.
Et par årtier senere faldt matematikeren Benoit Mandelbrot over Richardsons arbejde i en kasseret biblioteksbog, mens han arbejdede hos IBM. Han erkendte dets betydning, og også hvordan det hænger sammen med nyere forskning om fraktaler og dimensioner.
Den britiske kystlinje “ligner” bestemt en fraktal, men den er ikke selvlignende, som andre fraktaler, vi har set før. For at finde dens størrelse kan vi tegne den på et gitter og tælle antallet af celler, som den skærer den med.
I første omgang er der 88 celler, der skærer den. Hvis vi skalerer kystlinjen med en faktor 2, er der 197 celler, der skærer hinanden – mere end dobbelt så mange!
Størrelsen af kystlinjen er steget med en faktor 19788. Ligesom før betyder det, at kystlinjens dimension er
d=log219788≈1,16
Hvis vi gentager dette med større gitter, vil vi opdage, at dimensionen af Storbritanniens kystlinje faktisk er ca. 1,21. Mandelbrot indså, at denne fraktaldimension også er et mål for en forms ruhed – et nyt begreb, som han fandt vigtige anvendelser for inden for mange andre områder af matematik og videnskab.
Mere fraktaler i natur og teknologi
Selv om ægte fraktaler aldrig kan optræde i naturen, er der mange objekter, der næsten ligner fraktaler. Vi har allerede set planter, sneflager og kystlinjer, og her er nogle flere eksempler:
Bjergkæde i Centralasien
Ganges-flodens delta i Indien
Lynnedslag
Blodkar i nethinden
Grand Canyon i USA
Skyer
Alle disse objekter kan forekomme helt tilfældige, men ligesom fraktaler er der et underliggende mønster, der bestemmer, hvordan de er dannet. Matematik kan hjælpe os med at forstå formerne bedre, og fraktaler har anvendelser inden for områder som medicin, biologi, geologi og meteorologi.
Computergenereret fraktalt terræn
Vi kan også bruge fraktaler til at skabe realistiske “kopier” af naturen, f.eks. som landskaber og teksturer, der bruges i videospil eller computergenererede film. Vandet, bjergene og skyerne på dette billede er skabt udelukkende af en computer ved hjælp af fraktaler!
Og vi kan endda vende denne proces om og komprimere digitale billeder for at reducere deres filstørrelse. De første algoritmer blev udviklet af Michael Barnsley og Alan Sloan i 1980’erne, og der forskes stadig i nye algoritmer i dag.