Gleichungen der SHM
Betrachten Sie einen Block, der an einer Feder auf einem reibungsfreien Tisch befestigt ist (Abbildung \(\PageIndex{3}\)). Die Gleichgewichtslage (die Lage, in der die Feder weder gedehnt noch gestaucht ist) ist mit x = 0 gekennzeichnet. In der Gleichgewichtslage ist die Nettokraft gleich Null.
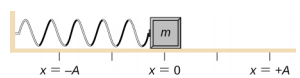
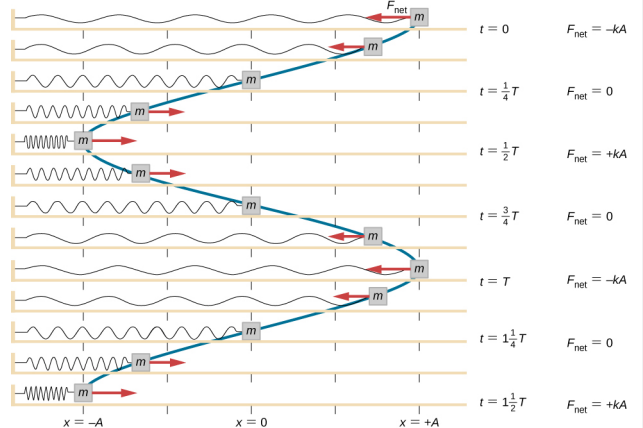
Der Klotz wird durch Arbeit in eine Lage von x = + A gezogen und dann aus der Ruhelage gelöst. Die maximale x-Position (A) wird als die Amplitude der Bewegung bezeichnet. Der Block beginnt in SHM zwischen x = + A und x = -A zu schwingen, wobei A die Amplitude der Bewegung und T die Periode der Schwingung ist. Die Periode ist die Zeit für eine Schwingung. Abbildung \(\PageIndex{4}\) zeigt die Bewegung des Blocks, wie er eineinhalb Schwingungen nach dem Loslassen vollführt.
\
Die Gleichung für die Position als Funktion der Zeit \(x(t) = A\cos( \omega t)\) eignet sich gut für die Modellierung von Daten, bei denen die Position des Klotzes zum Anfangszeitpunkt t = 0,00 s der Amplitude A entspricht und die Anfangsgeschwindigkeit Null ist. Bei experimentellen Daten ist die Position der Masse zum Anfangszeitpunkt t = 0,00 s oft nicht gleich der Amplitude und die Anfangsgeschwindigkeit ist nicht gleich Null. Betrachten Sie die von einem Schüler im Labor gesammelten Daten von 10 Sekunden, die in Abbildung \(\PageIndex{6}\) dargestellt sind.
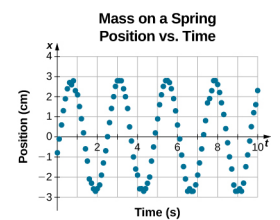
Die Daten in Abbildung \(\PageIndex{6}\) können immer noch mit einer periodischen Funktion, wie einer Kosinusfunktion, modelliert werden, aber die Funktion ist nach rechts verschoben. Diese Verschiebung wird als Phasenverschiebung bezeichnet und gewöhnlich durch den griechischen Buchstaben phi (\(\phi\)) dargestellt. Die Gleichung der Position als Funktion der Zeit für einen Block auf einer Feder lautet
\
Dies ist die verallgemeinerte Gleichung für SHM, wobei t die in Sekunden gemessene Zeit ist, \(\omega\) die Winkelfrequenz mit Einheiten von inversen Sekunden, A die in Metern oder Zentimetern gemessene Amplitude und \(\phi\) die in Bogenmaß gemessene Phasenverschiebung (Abbildung \(\PageIndex{7}\)). Da sich Sinus- und Kosinusfunktionen nur durch eine Phasenverschiebung unterscheiden, könnte diese Bewegung entweder mit der Kosinus- oder der Sinusfunktion modelliert werden.
Die Geschwindigkeit der Masse auf einer Feder, die in SHM schwingt, kann durch die Ableitung der Positionsgleichung ermittelt werden:
\
Da die Sinusfunktion zwischen -1 und +1 schwingt, ist die maximale Geschwindigkeit die Amplitude mal der Kreisfrequenz, vmax = A\(\omega\). Die maximale Geschwindigkeit tritt in der Gleichgewichtslage (x = 0) auf, wenn sich die Masse in Richtung x = + A bewegt. Die maximale Geschwindigkeit in negativer Richtung wird in der Gleichgewichtslage (x = 0) erreicht, wenn sich die Masse in Richtung x = -A bewegt, und ist gleich -vmax.
Die Beschleunigung der Masse auf der Feder kann durch die zeitliche Ableitung der Geschwindigkeit ermittelt werden:
\