Berechnung von ΔS aus thermodynamischen Zyklen
Wir können eine Entropieänderung auch mit Hilfe eines thermodynamischen Zyklus berechnen. Wie du bereits gelernt hast, ist die molare Wärmekapazität (Cp) die Wärmemenge, die benötigt wird, um die Temperatur von 1 Mol eines Stoffes bei konstantem Druck um 1°C zu erhöhen. Analog dazu ist Cv die Wärmemenge, die benötigt wird, um die Temperatur von 1 Mol eines Stoffes bei konstantem Volumen um 1 °C zu erhöhen. Die Zunahme der Entropie mit steigender Temperatur in Abbildung \(\PageIndex{2}\) ist annähernd proportional zur Wärmekapazität des Stoffes.
Erinnern Sie sich, dass die Entropieänderung (ΔS) mit dem Wärmestrom (qrev) durch ΔS = qrev/T verbunden ist. Da qrev = nCpΔT bei konstantem Druck oder nCvΔT bei konstantem Volumen ist, wobei n die Anzahl der Mole der vorhandenen Substanz ist, ist die Entropieänderung für eine Substanz, deren Temperatur sich von T1 zu T2 ändert, wie folgt:
\
Wie Sie in fortgeschritteneren Mathematikkursen, als sie hier erforderlich sind, entdecken werden, kann gezeigt werden, dass dies gleich dem Folgenden ist:Für eine Übersicht über natürliche Logarithmen, siehe Grundlegende Fähigkeiten 6 in Kapitel 11 „Flüssigkeiten“.
\
Also können wir eine Kombination von Wärmekapazitätsmessungen (Gleichung 18.20 oder Gleichung 18.21) und experimentell gemessenen Werten von Schmelz- oder Verdampfungsenthalpien verwenden, wenn eine Phasenänderung beteiligt ist (Gleichung 18.18), um die Entropieänderung zu berechnen, die einer Temperaturänderung einer Probe entspricht.
Wir können einen thermodynamischen Zyklus verwenden, um die Entropieänderung zu berechnen, wenn die Phasenänderung für eine Substanz wie Schwefel nicht direkt gemessen werden kann. Wie in der Übung in Beispiel 6 erwähnt, existiert elementarer Schwefel in zwei Formen (Teil (a) in Abbildung \(\PageIndex{3}\)): eine orthorhombische Form mit einer hoch geordneten Struktur (Sα) und eine weniger geordnete monokline Form (Sβ). Die orthorhombische (α) Form ist bei Raumtemperatur stabiler, geht aber bei Temperaturen über 95,3 °C (368,5 K) in die monokline (β) Form über. Der Übergang von Sα zu Sβ kann durch den thermodynamischen Zyklus beschrieben werden, der in Teil (b) in Abbildung \(\PageIndex{3}\) dargestellt ist und bei dem flüssiger Schwefel ein Zwischenprodukt ist. Die Entropieänderung, die mit der Umwandlung von flüssigem Schwefel in Sβ einhergeht (-ΔSfus(β) = ΔS3 im Zyklus), kann nicht direkt gemessen werden. Da die Entropie jedoch eine Zustandsfunktion ist, kann ΔS3 aus der Gesamtentropieänderung (ΔSt) für den Sα-Sβ-Übergang berechnet werden, die der Summe der ΔS-Werte für die Schritte im thermodynamischen Zyklus entspricht, wobei Gleichung 18.20 und die tabellierten thermodynamischen Parameter (die Wärmekapazitäten von Sα und Sβ, ΔHfus(α) und der Schmelzpunkt von Sα.)

Die Lösung für ΔS3 ergibt einen Wert von -3,24 J/(mol-K). Wie für die Umwandlung eines weniger geordneten Zustands (einer Flüssigkeit) in einen stärker geordneten (einen Kristall) zu erwarten, ist ΔS3 negativ.
Wie werden Entropien gemessen
Die absolute Entropie einer Substanz bei einer Temperatur über 0 K muss bestimmt werden, indem die Wärmemengen q berechnet werden, die erforderlich sind, um die Substanz von 0 K auf die interessierende Temperatur zu bringen, und dann die Verhältnisse q/T summiert werden. Zwei Arten von experimentellen Messungen sind erforderlich:
- Die Enthalpien, die mit allen Phasenänderungen verbunden sind, die der Stoff innerhalb des interessierenden Temperaturbereichs durchlaufen kann. Das Schmelzen eines Feststoffs und das Verdampfen einer Flüssigkeit entsprechen einer beträchtlichen Zunahme der Zahl der Mikrozustände, die für die Aufnahme von Wärmeenergie zur Verfügung stehen. Wenn diese Prozesse stattfinden, fließt also Energie in ein System und füllt diese neuen Mikrozustände in dem Maße auf, das erforderlich ist, um eine konstante Temperatur (den Gefrier- oder Siedepunkt) aufrechtzuerhalten; diese Zuflüsse von Wärmeenergie entsprechen den Schmelz- und Verdampfungswärmen. Die mit dem Schmelzen verbundene Entropieerhöhung beträgt beispielsweise nur ΔHfusion/Tm.
- Die Wärmekapazität C einer Phase drückt die Wärmemenge aus, die erforderlich ist, um die Temperatur um einen kleinen Betrag ΔT oder genauer gesagt um einen infinitesimalen Betrag dT zu ändern. Die Entropieerhöhung, die durch die Erwärmung eines Stoffes über einen Temperaturbereich, der keinen Phasenübergang umfasst, verursacht wird, ist also durch die Summe der Größen C dT/T für jeden Temperaturschritt dT gegeben. Dies ist natürlich nur das Integral
\
Da die Wärmekapazität selbst geringfügig temperaturabhängig ist, ist es für die genaueste Bestimmung der absoluten Entropien erforderlich, dass die funktionale Abhängigkeit von C von T in dem obigen Integral anstelle eines konstanten C verwendet wird.
\
Wenn dies nicht bekannt ist, kann man eine Reihe von Wärmekapazitätsmessungen über enge Temperaturschritte ΔT durchführen und die Fläche unter jedem Abschnitt der Kurve messen.
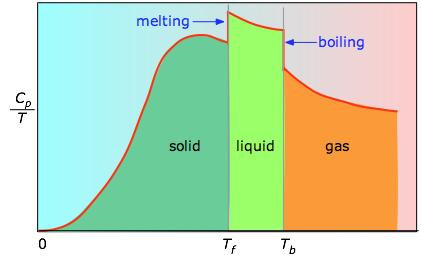
Die Fläche unter jedem Abschnitt des Diagramms stellt die Entropieänderung dar, die mit der Erwärmung der Substanz über ein Intervall ΔT verbunden ist. Dazu kommen die Schmelzenthalpien, die Verdampfungsenthalpien und die Enthalpien der Festkörper-Phasenwechsel. Die Werte von Cp für Temperaturen nahe Null werden nicht direkt gemessen, sondern können anhand der Quantentheorie geschätzt werden.
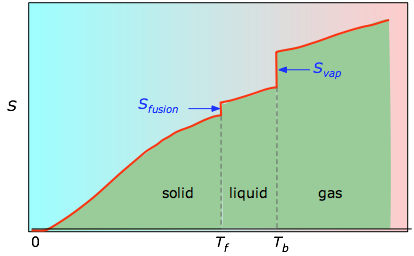
Die kumulativen Flächen von 0 K bis zu einer beliebigen Temperatur (aus der experimentellen Darstellung links) werden dann als Funktion von T aufgetragen, und alle Phasenänderungsentropien wie Svap = Hvap / Tb werden addiert, um die absolute Entropie bei Temperatur T zu erhalten.