Faktorielle Zahlen findet man überall in der Kombinatorik, weil sie dort ihren Ursprung haben. Die Fakultät wurde geschaffen, um die Anzahl der Anordnungen einer Gruppe von Gegenständen auszudrücken, die wir natürlich in ihrer grundlegendsten Form mit Hilfe der Multiplikationsregel des Zählens finden.
Die Fakultät ist sozusagen die inoffizielle Operation der Multiplikationsregel des Zählens.
Warum die Fakultät Null gleich 1 ist
Hier wird es knifflig, denn wenn wir an die Fakultäten nur in dem Kontext denken, in dem sie normalerweise definiert werden, d. h. als das „Produkt aller Zahlen“.d.h. das „Produkt aller positiven ganzen Zahlen, die kleiner oder gleich der Zahl sind“, dann ist es, als ob man mit 0! gegen eine Mauer stößt.
Die meisten Leute werden dir sagen, dass 0! als 1 definiert ist, und wenn du fragst, warum, sagen sie einfach „weil es als 1 definiert ist“.
Ja, das ist ziemlich frustrierend. Das ist das mathematische Äquivalent dazu, wenn du deine Eltern fragst, warum du dich an eine willkürliche Regel halten musst, die sie aufgestellt haben, und sie dir sagen: „Weil ich es so gesagt habe.“
Das mag zwar eine akzeptierte Erziehungsmethode sein, aber es ist eine miserable Art, Mathematik zu lernen. Worum geht’s also? Wie haben wir entschieden, dass die Nullfaktorialität gleich eins ist?
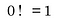
Ein intuitives Verständnis
Erinnern Sie sich daran, wie wir sagten, dass die Faktorialität aus der mathematischen Operation stammt, die Anzahl der Permutationen oder Anordnungen einer Menge zu finden? (Anmerkung: nicht die Permutationen einer kleineren Menge aus einer größeren Menge, sondern nur die Anordnungen einer gegebenen Menge.)
Die Fakultät Null kann man sich als die Anzahl der Anordnungen von Nullelementen in einer Menge vorstellen, auch bekannt als die leere Menge {}. (Wenn Sie sich jemals mit Mengen beschäftigt haben, vielleicht in den Grundlagen der Statistik oder der diskreten Mathematik, sind Sie wahrscheinlich mit dem Konzept der leeren Menge vertraut. Es ist buchstäblich die Menge des Nichts.)
Wenn ich Sie nun fragen würde, wie viele Anordnungen es von einer Sache gibt, würden Sie 1 antworten, weil es nur eine Möglichkeit gibt, eine Sache anzuordnen. Die gleiche Idee folgt hier. Unsere „eine Sache“ ist die leere Menge, und die Anzahl der Anordnungen der leeren Menge ist eins. Das war’s. Deshalb ist 0! gleich 1.
Wie man faktorielle Ausdrücke vereinfacht
Nun, da wir die Grundlagen hinter uns haben, ist es Zeit für das Herzstück unseres faktoriellen Tutorials: das Vereinfachen.
Die beste Art, Mathematik zu sehen, ist in Aktion. Ich führe euch also durch die sechs Aufgaben, die in der Abbildung oben in diesem Beitrag zu sehen sind! Wir fangen ganz einfach an, gehen dann zur Kombinationsformel mit Zahlen und Variablen über und enden mit einigen kniffligeren faktoriellen Ausdrücken.
❤ STAY CONNECTED ❤
Verpasse keinen Beat oder ein mathematisches Problem!