Halbwertszeit

Abbildung 1. Ein Diagramm, das den Zerfall eines radioaktiven Kerns im Laufe der Zeit zeigt. Die Zeit, die die Masse oder Aktivität der Quelle (die Anzahl der Zerfallsereignisse pro Sekunde) benötigt, um auf die 50%-Marke zu fallen, ist die Halbwertszeit. Die Halbwertszeit in diesem Bild beträgt 1 Jahr.

Die Halbwertszeit ist die Zeit, die es dauert, bis die Hälfte des ursprünglichen Wertes einer bestimmten Menge eines radioaktiven Elements zerfällt. Außerdem ist eine Halbwertszeit die Zeit, die vergeht, bis die Aktivität einer Quelle auf die Hälfte ihres ursprünglichen Wertes gesunken ist. Der zweite Hauptsatz der Thermodynamik, insbesondere die Aussage über die Unordnung, kann dazu beitragen, zu verstehen, warum radioaktiver Zerfall stattfindet. Dieser Satz besagt, dass die Entropie eines geschlossenen Systems niemals abnehmen kann, was bedeutet, dass die Dinge weiter in die Unordnung und nicht in die Ordnung fallen müssen. Dieser Prozess wird als „Zerfall“ bezeichnet, und das zweite Gesetz hilft zu erklären, warum Materie im Laufe der Zeit in einen immer weniger organisierten Zustand zerfällt. Teil dieses Prozesses sind bestimmte Arten von Atomen, die mit einer messbaren Rate, die als radioaktiver Zerfall bezeichnet wird, in neue, andere Arten von Atomen zerfallen.

Alle radioaktiven Materialien haben instabile Kerne in sich. Zusätzlich gibt es auch einige Kerne in der Substanz, die sich bereits im stabilen Zustand befinden, aber das Verhältnis von stabilen zu instabilen Kernen in einer Probe kann variieren. Die stabilen Kerne in der Probe sind unveränderlich (und befinden sich in einem stabilen energetischen Zustand), aber die instabilen Kerne werden im Laufe der Zeit eine Art Kernzerfall durchlaufen, um stabil zu werden. Dies führt zur Emission einer bestimmten Form von Strahlung. Da die Halbwertszeit ein Maß für die Zeit ist, ist die Halbwertszeit ein Wert, der angibt, wie lange dieser Übergang zu einem stabileren Energiezustand dauert.

Bei verschiedenen Substanzen geht die Radioaktivität schneller verloren als bei anderen. Bei einigen radioaktiven Elementen kann die Hälfte der instabilen Kerne in weniger als einer Sekunde zerfallen. Krypton-101 zum Beispiel hat eine Halbwertszeit von etwa einer zehnmillionstel Sekunde. Im Gegensatz dazu haben einige Elemente außerordentlich lange Halbwertszeiten und benötigen Milliarden von Jahren, um zu zerfallen. Uran-238 hat eine Halbwertszeit von 4,51 Milliarden Jahren. Das bedeutet, dass es Milliarden von Jahren dauern würde, bis Uran-238 in ein Verhältnis von halb Uran-238 und halb Thorium-234 zerfallen würde. Uran-235 (ein weiteres natürlich vorkommendes Isotop des Urans) hat eine kürzere Halbwertszeit als Uran-238, nämlich nur ~700 Millionen Jahre.

Gleichung

Es gibt eine Gleichung, die häufig verwendet wird, um zu bestimmen, wie viel von einer bestimmten radioaktiven Substanz nach Ablauf einer bestimmten Zeit übrig bleibt. Dies wird anhand von Eigenschaften wie der Halbwertszeit der Substanz und der ursprünglichen Menge der Substanz bestimmt. Die verwendete Gleichung lautet:

wobei:

• die Menge der Substanz nach Ablauf der Zeit ist
• die anfängliche Menge der Substanz ist
• die verstrichene Zeit ist
• die Halbwertszeit der Substanz ist

Außerdem kann eine ähnliche Gleichung verwendet werden, um zu zeigen, wie die Aktivität der Substanz mit der Zeit abnimmt. In diesem Fall hat die Gleichung die Form:

wobei:

• die Aktivität der Substanz nach Ablauf der Zeit ist
• die anfängliche Aktivität der Substanz ist
• die verstrichene Zeit ist
• die Halbwertszeit der Substanz ist

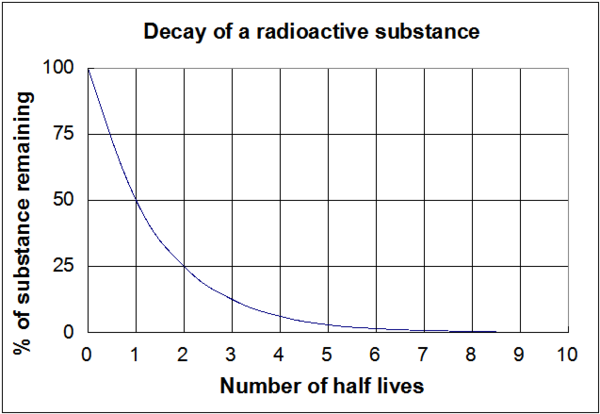
Das in Abbildung 1 dargestellte Diagramm ist eine visuelle Darstellung dieser Gleichungen. Es ist wichtig zu beachten, dass unabhängig von der tatsächlichen Länge der Halbwertszeit (ob sie Millionen von Jahren oder einige Nanosekunden beträgt) die Form des Graphen die gleiche ist.

Die Kenntnis der Halbwertszeiten ist Teil der Methode, mit der Geologen Gesteine mit Hilfe der Radioisotopen-Datierung datieren.