Ein Arbeitsmedium enthält potentielle Energie (Druckhöhe) und kinetische Energie (Geschwindigkeitshöhe). Das Fluid kann kompressibel oder inkompressibel sein. Turbinen nutzen mehrere physikalische Prinzipien zur Gewinnung dieser Energie:
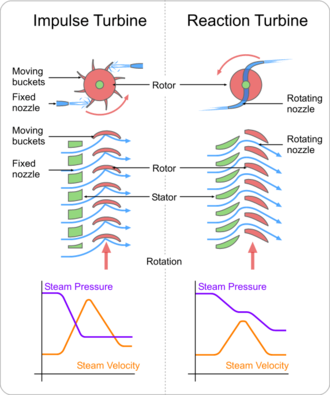
Impulsturbinen ändern die Strömungsrichtung eines Hochgeschwindigkeitsfluids oder eines Gasstrahls. Der resultierende Impuls treibt die Turbine an und verlässt den Flüssigkeitsstrom mit verminderter kinetischer Energie. In den Turbinenschaufeln (den sich bewegenden Schaufeln) findet keine Druckänderung des Fluids oder Gases statt, wie dies bei einer Dampf- oder Gasturbine der Fall ist; der gesamte Druckabfall findet in den stationären Schaufeln (den Düsen) statt. Vor Erreichen der Turbine wird die Druckhöhe des Fluids durch Beschleunigung des Fluids mit einer Düse in eine Geschwindigkeitshöhe umgewandelt. Peltonräder und de Laval-Turbinen verwenden ausschließlich dieses Verfahren. Impulsturbinen benötigen keinen Druckmantel um den Rotor, da der Flüssigkeitsstrahl durch die Düse erzeugt wird, bevor er die Schaufeln des Rotors erreicht. Das zweite Newtonsche Gesetz beschreibt die Energieübertragung bei Impulsturbinen. Impulsturbinen sind dort am effizientesten, wo der Durchfluss gering und der Eingangsdruck hoch ist.
Reaktionsturbinen entwickeln ein Drehmoment, indem sie auf den Druck oder die Masse des Gases oder der Flüssigkeit reagieren. Der Druck des Gases oder der Flüssigkeit ändert sich beim Durchströmen der Turbinenlaufschaufeln. Ein Druckgehäuse ist erforderlich, um das Arbeitsmedium aufzufangen, während es auf die Turbinenstufe(n) einwirkt, oder die Turbine muss vollständig in den Flüssigkeitsstrom eingetaucht werden (wie bei Windkraftanlagen). Das Gehäuse enthält und leitet das Arbeitsmedium und hält bei Wasserturbinen den vom Saugrohr erzeugten Sog aufrecht. Francis-Turbinen und die meisten Dampfturbinen verwenden dieses Konzept. Bei kompressiblen Arbeitsflüssigkeiten werden in der Regel mehrere Turbinenstufen verwendet, um das expandierende Gas effizient zu nutzen. Das dritte Newtonsche Gesetz beschreibt die Energieübertragung bei Reaktionsturbinen. Reaktionsturbinen eignen sich besser für höhere Strömungsgeschwindigkeiten oder für Anwendungen, bei denen die Förderhöhe (der Druck vor der Turbine) gering ist.
Bei Dampfturbinen, wie sie in der Schifffahrt oder bei der Stromerzeugung an Land eingesetzt werden, würde eine Reaktionsturbine vom Typ Parsons für den gleichen Grad an thermischer Energieumwandlung etwa doppelt so viele Schaufelreihen benötigen wie eine Impulsturbine vom Typ de Laval. Dadurch wird die Parsons-Turbine zwar viel länger und schwerer, aber der Gesamtwirkungsgrad einer Reaktionsturbine ist bei gleicher thermischer Energieumwandlung etwas höher als der einer entsprechenden Impulsturbine.
In der Praxis werden bei modernen Turbinenkonstruktionen, wann immer möglich, sowohl Reaktions- als auch Impulskonzepte in unterschiedlichem Maße eingesetzt. Windturbinen verwenden ein Tragflächenprofil, um einen Reaktionsauftrieb aus der sich bewegenden Flüssigkeit zu erzeugen und diesen auf den Rotor zu übertragen. Windturbinen gewinnen auch etwas Energie aus dem Impuls des Windes, indem sie ihn in einem Winkel ablenken. Mehrstufige Turbinen können entweder Reaktions- oder Impulsbeschaufelung bei hohem Druck verwenden. Dampfturbinen waren traditionell eher impulsbetrieben, gehen aber immer mehr zu reaktionsbetriebenen Konstruktionen über, ähnlich denen, die in Gasturbinen verwendet werden. Bei niedrigem Druck vergrößert sich das Volumen des Betriebsmediums bei geringen Druckabfällen. Unter diesen Bedingungen wird die Beschaufelung zu einem reinen Reaktionstyp, bei dem die Basis der Schaufel ausschließlich impulsartig ist. Der Grund dafür ist die Auswirkung der Rotationsgeschwindigkeit der einzelnen Schaufeln. Mit zunehmender Lautstärke nimmt die Schaufelhöhe zu, und der Fuß der Schaufel dreht sich mit einer geringeren Geschwindigkeit als die Spitze. Diese Geschwindigkeitsänderung zwingt den Konstrukteur, von einem Impuls an der Basis zu einer reaktionsschnellen Spitze überzugehen.
Die klassischen Methoden der Turbinenkonstruktion wurden Mitte des 19. Jahrhunderts entwickelt. Die Vektoranalyse setzte die Strömung mit der Turbinenform und der Rotation in Beziehung. Zunächst wurden grafische Berechnungsmethoden verwendet. Die Formeln für die grundlegenden Abmessungen der Turbinenteile sind gut dokumentiert, und eine hocheffiziente Maschine kann für jede Strömungsbedingung zuverlässig ausgelegt werden. Einige der Berechnungen sind empirische Formeln oder Faustformeln, andere basieren auf der klassischen Mechanik. Wie bei den meisten technischen Berechnungen wurden vereinfachende Annahmen getroffen.

Geschwindigkeitsdreiecke können zur Berechnung der grundlegenden Leistung einer Turbinenstufe verwendet werden. Das Gas tritt mit der absoluten Geschwindigkeit Va1 aus den stationären Turbinenleitschaufeln aus. Der Rotor dreht sich mit der Geschwindigkeit U. Relativ zum Rotor beträgt die Geschwindigkeit des Gases beim Auftreffen auf den Rotoreingang Vr1. Das Gas wird durch den Rotor gedreht und tritt relativ zum Rotor mit der Geschwindigkeit Vr2 aus. Absolut gesehen beträgt die Rotoraustrittsgeschwindigkeit jedoch Va2. Die Geschwindigkeitsdreiecke werden mit Hilfe dieser verschiedenen Geschwindigkeitsvektoren konstruiert. Die Geschwindigkeitsdreiecke können an jedem beliebigen Abschnitt der Beschaufelung konstruiert werden (z. B. Nabe, Spitze, Mittelteil usw.), werden aber normalerweise am mittleren Stufenradius dargestellt. Die mittlere Leistung der Stufe kann aus den Geschwindigkeitsdreiecken an diesem Radius mit Hilfe der Euler-Gleichung berechnet werden:
Δ h = u ⋅ Δ v w {\displaystyle \Delta h=u\cdot \Delta v_{w}}

Hieraus:
Δ h T = u ⋅ Δ v w T {\displaystyle {\frac {\Delta h}{T}}={\frac {u\cdot \Delta v_{w}}{T}}

wobei:
Δ h {\displaystyle \Delta h}

ist der spezifische Enthalpieabfall über die Stufe T {\displaystyle T}

ist die Gesamteintritts- (oder Stagnations-) Temperatur der Turbine u {\displaystyle u}

ist die Umfangsgeschwindigkeit des Turbinenrotors Δ v w {\displaystyle \Delta v_{w}}

ist die Änderung der Wirbelgeschwindigkeit
Das Turbinendruckverhältnis ist eine Funktion von Δ h T {\displaystyle {\frac {\Delta h}{T}}

und dem Turbinenwirkungsgrad.
Modernes Turbinendesign führt die Berechnungen weiter. Die numerische Strömungsdynamik macht viele der vereinfachenden Annahmen überflüssig, die zur Ableitung der klassischen Formeln verwendet wurden, und die Computersoftware erleichtert die Optimierung. Diese Werkzeuge haben in den letzten vierzig Jahren zu einer ständigen Verbesserung der Turbinenkonstruktion geführt.
Die wichtigste numerische Klassifizierung einer Turbine ist ihre spezifische Drehzahl. Diese Zahl beschreibt die Geschwindigkeit der Turbine bei maximalem Wirkungsgrad in Bezug auf die Leistung und den Durchfluss. Die spezifische Drehzahl wird als unabhängig von der Turbinengröße abgeleitet. Ausgehend von den Strömungsbedingungen und der gewünschten Abtriebsdrehzahl der Welle kann die spezifische Drehzahl berechnet und eine geeignete Turbinenkonstruktion ausgewählt werden.
Die spezifische Drehzahl kann zusammen mit einigen grundlegenden Formeln verwendet werden, um eine bestehende Konstruktion mit bekannter Leistung zuverlässig auf eine neue Größe mit entsprechender Leistung zu skalieren.
Die Leistung außerhalb der Auslegung wird normalerweise als Turbinenkennfeld oder -charakteristik dargestellt.
Die Anzahl der Schaufeln im Rotor und die Anzahl der Leitschaufeln im Stator sind oft zwei verschiedene Primzahlen, um die Oberwellen zu reduzieren und die Schaufeldurchgangsfrequenz zu maximieren.