Eventos dependientes vs independientes
Hace un par de posts comencé a hablar de las probabilidades. Quiero dedicar un poco más de tiempo al tema porque es uno de esos conceptos que pueden ser obviamente fáciles en un minuto y francamente confusos al siguiente.
Cuando se aborda un problema de probabilidad que implica más de un suceso se empieza preguntando si los sucesos son dependientes o independientes, es decir, ¿altera un suceso la probabilidad del otro suceso? (Sacar varias cartas de una baraja sin reemplazo es un ejemplo clásico de suceso dependiente. Cuando sacamos la primera carta, el sistema cambia de 52 opciones posibles a 51 antes de que ocurra el segundo suceso.)
En la vida real, los humanos tienen la tendencia a confundir la dependencia todo el tiempo. Por ejemplo, usted lanza una moneda justa. Sale cara 10 veces seguidas. Estás seguro de que la próxima vez saldrá cruz… ¿no?
¿Cuál es la probabilidad de que la próxima moneda salga cara otra vez?
Sigue siendo 1/2. Lanzar una moneda es un evento independiente. Es decir, el resultado de la siguiente tirada no está influenciado por lo que ha ocurrido anteriormente. Es como si fuera la primera vez que se lanza la moneda. La probabilidad no se altera.
¿Por qué se «siente» que debería ser cruz entonces?
Tendemos a pensar en los eventos juntos, en lugar de individualmente. Aunque la probabilidad de sacar cara sigue siendo la misma en cada lanzamiento, la posibilidad combinada de sacar 11 caras seguidas es pequeña.
Calculemosla.
Aprendimos en la lección de probabilidad anterior que cuando encadenamos varios sucesos y queremos que todos ocurran (el escenario «y») debemos multiplicar sus probabilidades juntas.
Como cada lanzamiento de una moneda tiene una probabilidad de salir cara igual a 1/2, simplemente tengo que multiplicar juntos 1/2 once veces.
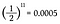
¡Eso es un 0,05% de probabilidad de sacar once caras seguidas! Pero antes de que exhale un suspiro de alivio y diga: «¡Ves, lo sabía!», calculemos la probabilidad de obtener una cola en el undécimo lanzamiento.
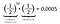
Sí, es cierto. Es igual de probable sacar diez caras seguidas de una cola que sacar once caras seguidas. De hecho, como la probabilidad individual de sacar cara es la misma que la de sacar cruz, cada disposición de 11 lanzamientos de la moneda tendrá la misma probabilidad de 0,0005. Cada disposición es igualmente probable.
Entonces… ¿por qué «parece» improbable sacar diez caras seguidas??
El error común no está causado por la probabilidad, sino por un malentendido de la combinatoria y las permutaciones.
Hasta ahora hemos establecido que:
- La probabilidad de sacar cara o cruz es igualmente probable en cada lanzamiento individual: P(H) = P(T) = 1/2.
- Cada arreglo único (permutación) de posibles lanzamientos de monedas es igualmente probable.
¿Entonces qué pasa?
Entendiendo el espacio muestral
El espacio muestral es simplemente un listado de todos los posibles arreglos de resultados (permutaciones). Dado que el espacio muestral para 11 lanzamientos consecutivos de monedas es bastante grande, vamos a examinar un caso más simple en su lugar.
El espacio muestral para cuatro lanzamientos de monedas es:

Intuitivamente, podríamos pensar: es más probable que salgan 2 caras y 2 colas de cuatro lanzamientos que todas las caras o todas las colas.
Y esto es cierto. Hagamos las cuentas.
Sabemos que cada una de las dieciséis permutaciones tiene la misma probabilidad porque P(H) = P(T) = 1/2. Así que cada permutación tiene una probabilidad igual de:

Nota: Como el espacio muestral representa todos los resultados posibles, la suma de todas las probabilidades siempre es igual a 1 (Por ejemplo, 0,0625 – 16 = 1).
Mirando nuestro espacio muestral, ¿cuántas permutaciones diferentes de lanzamiento de monedas dan como resultado cualquier combinación 0de 2 caras y 2 colas?

Nótese que 6 de los 16 resultados posibles dan como resultado una combinación de dos caras/dos colas. Debido a que cualquiera de esas seis permutaciones cumple con nuestros criterios, esto se considera un escenario «o» – por lo que se suman las probabilidades (o simplemente se multiplican por 6 ya que son todas iguales).
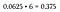
Eso es una probabilidad del 37,5% de lanzar una combinación de 2 caras y 2 colas, que es mucho mayor que la probabilidad de lanzar todas las caras o todas las colas (que sigue siendo del 6.Esto es por lo que intuitivamente sabemos que es más probable lanzar un número igual de caras y colas, que lanzar todas de un mismo tipo, mientras se mantiene el hecho de que los eventos son independientes con lanzamientos individuales y permutaciones igualmente probables.
Permutaciones &Combinaciones
Mucho del éxito en el cálculo de probabilidades es la comprensión de las permutaciones y combinaciones a fondo. Así que ahí es donde nos dirigimos a continuación.