Harmonisen liikkeen yhtälöt
Tarkastellaan palikkaa, joka on kiinnitetty jousen varaan kitkattomalle pöydälle (kuva \(\PageIndex{3}\)). Tasapainoasento (asento, jossa jousi ei ole venytetty eikä puristettu) on merkitty x = 0 . Tasapainoasennossa nettovoima on nolla.
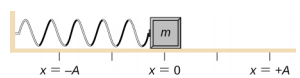
Lohkolle tehdään työ, jolla se vedetään asentoon x = + A, minkä jälkeen se vapautetaan levosta. Suurinta x-asentoa (A) kutsutaan liikkeen amplitudiksi. Lohko alkaa värähtelemään SHM:ssä välillä x = + A ja x = -A, missä A on liikkeen amplitudi ja T on värähtelyn jakso. Jakso on yhden värähtelyn kesto. Kuvassa \(\PageIndex{4}\) näkyy lohkon liike, kun se suorittaa puolitoista värähtelyä vapautuksen jälkeen.
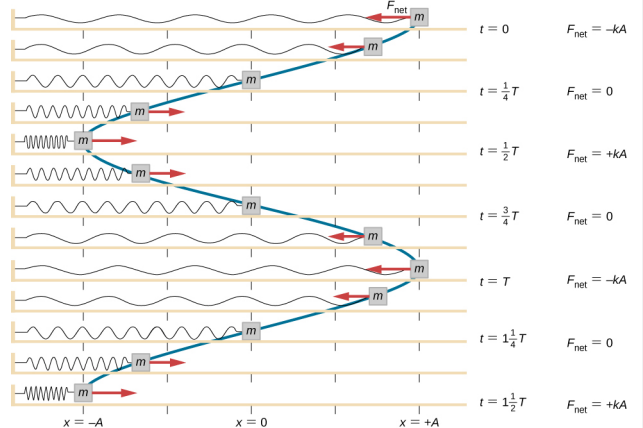
\
Yhtälö sijainnille ajan funktiona \(x(t) = A\cos( \omega t)\) soveltuu hyvin mallinnettavaksi aineistosta, jossa lohkon sijainti alkuajankohtana t = 0,00 s on amplitudilla A ja alkunopeus on nolla. Usein kokeellisia tietoja otettaessa massan sijainti alkuajankohtana t = 0,00 s ei ole yhtä suuri kuin amplitudi ja alkunopeus ei ole nolla. Tarkastellaan opiskelijan laboratoriossa keräämää 10 sekunnin dataa, joka näkyy kuvassa \(\PageIndex{6}\).
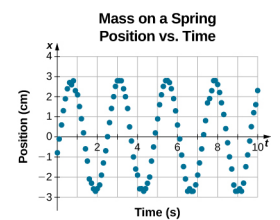
Kuvan \(\PageIndex{6}\) dataa voidaan edelleen mallintaa jaksollisella funktiolla, kuten kosinifunktiolla, mutta funktio on siirretty oikealle. Tätä siirtymää kutsutaan vaihesiirtymäksi, ja se esitetään yleensä kreikkalaisella kirjaimella phi (\(\phi\)). Jousella olevan kappaleen sijainnin yhtälö ajan funktiona on
\\
Tämä on SHM:n yleistetty yhtälö, jossa t on aika sekunneissa mitattuna, \(\omega\) on kulmataajuus käänteissekunneissa, A on amplitudi metreissä tai senttimetreissä mitattuna ja \(\phi\) on vaiheensiirtymä radiaaneissa mitattuna (kuva \(\(\Sivun indeksi{7}\)). On huomattava, että koska sini- ja kosinifunktiot eroavat toisistaan vain vaiheensiirrolla, tämä liike voitaisiin mallintaa joko kosini- tai sinifunktion avulla.
SHM:ssä värähtelevän jousella olevan massan nopeus voidaan löytää ottamalla paikkayhtälön derivaatta:
\\
Koska sinifunktio värähtelee -1:n ja +1:n välillä, maksiminopeus on amplitudi kertaa kulmataajuus, vmax = A\(\omega\). Maksiminopeus saavutetaan tasapainoasennossa (x = 0), kun massa liikkuu kohti x = + A. Maksiminopeus negatiiviseen suuntaan saavutetaan tasapainoasennossa (x = 0), kun massa liikkuu kohti x = -A, ja se on yhtä suuri kuin -vmax.
Massan kiihtyvyys jousen varassa saadaan selville ottamalla nopeuden aikaderivaatta:
\