Logistinen yhtälö (joskus Verhulstin malli tai logistinen kasvukäyrä) on Pierre Verhulstin (1845, 1847) ensimmäisenä julkaisema malli väestönkasvusta. Malli on ajallisesti jatkuva, mutta jatkuvan yhtälön muunnos diskreetiksi kvadraattiseksi rekursioyhtälöksi, joka tunnetaan nimellä logistinen kartta, on myös laajalti käytössä.
Logistisen mallin jatkuvaa versiota kuvaa differentiaaliyhtälö
 |
(1)
|
, jossa 
on malthusilainen parametri (väestön maksimikasvun vauhti) ja 
ns. kantavuuskapasiteetti (ts, suurin kestävä väestömäärä). Jakamalla molemmat puolet 
:llä ja määrittelemällä 
saadaan tällöin differentiaaliyhtälö
 |
(2)
|
joka tunnetaan seuraavasti kutsutaan logistiseksi yhtälöksi ja sillä on ratkaisu
 |
(3)
|
Funktiota 
kutsutaan joskus sigmoidifunktioksi.
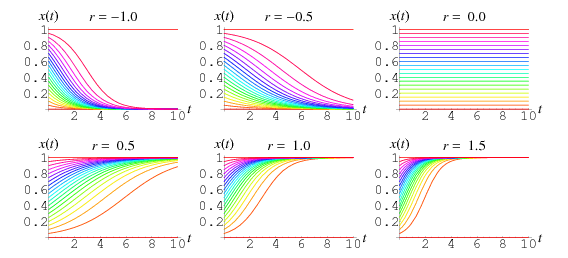
Mikäli 
on yleensä rajoitettu positiiviseksi, edellä esitetyn ratkaisun kuvaajat on esitetty 
:n eri positiivisille ja negatiivisille arvoille ja alkuehdoille 
, jotka vaihtelevat 0,00:sta 1,00:een 0,05:n askelin.
Logistisen yhtälön (3) diskreetti versio tunnetaan logistisena karttana.
Käyrää
 |
(4)
|
, joka saadaan yhtälöstä (3), sanotaan toisinaan logistiseksi käyräksi. Vastaavasti yhtälön (3) normalisoitua muotoa käytetään yleisesti tilastollisena jakaumana, joka tunnetaan nimellä logistinen jakauma.