Puoliintumisaika

Kuva 1. Kaavio, jossa esitetään radioaktiivisen ytimen hajoaminen ajan kuluessa. Aika, jonka kuluessa lähteen massa tai aktiivisuus (hajoamistapahtumien määrä sekunnissa) laskee 50 prosentin tasolle, on puoliintumisaika. Puoliintumisaika on tässä kuvassa 1 vuosi.

Puoliintumisaika on aika, joka kuluu siihen, että jonkin radioaktiivisen alkuaineen määrästä hajoaa puolet alkuperäisestä arvosta. Lisäksi yksi puoliintumisaika on aika, joka kuluu siihen, että jonkin lähteen aktiivisuus laskee puoleen alkuperäisestä arvosta. Termodynamiikan toista lakia, erityisesti epäjärjestyslauseketta, voidaan käyttää ymmärtämään, miksi radioaktiivista hajoamista tapahtuu. Tämän lauseen mukaan suljetun systeemin entropia ei voi koskaan pienentyä, mikä tarkoittaa, että asioiden on vajottava yhä enemmän epäjärjestykseen, ei järjestykseen. Tämä prosessi tunnetaan nimellä ”hajoaminen”, ja toinen laki auttaa selventämään, miksi aine hajoaa ajan myötä yhä vähemmän järjestäytyneeseen tilaan. Osa tätä prosessia ovat tietyntyyppiset atomit, jotka hajoavat uusiksi, erityyppisiksi atomeiksi jollakin mitattavissa olevalla nopeudella, joka tunnetaan nimellä radioaktiivinen hajoaminen.

Kaikki radioaktiiviset aineet sisältävät epävakaita ytimiä. Lisäksi aineen sisällä on myös joitakin ytimiä, jotka ovat jo vakaassa tilassaan, mutta vakaiden ja epästabiilien ytimien suhde näytteessä voi vaihdella. Näytteessä olevat vakaat ytimet ovat muuttumattomia (ja vakaassa energiatilassa), mutta epävakaat ytimet käyvät läpi jonkinlaisen ydinhajoamisen ajan kuluessa muuttuakseen vakaiksi. Tämän seurauksena syntyy jonkinlaista säteilyä. Koska puoliintumisaika on ajan mitta, puoliintumisaika on arvo, joka määrittää, kuinka kauan tämä hajoaminen vakaampaan energiatilaan kestää.

Erilaiset aineet menettävät radioaktiivisuutensa nopeammin kuin toiset. Joidenkin radioaktiivisten alkuaineiden epävakaista ytimistä puolet voi hajota alle sekunnissa. Esimerkiksi krypton-101:n puoliintumisaika on noin sekunnin kymmenmiljoonasosa. Sen sijaan joillakin alkuaineilla on poikkeuksellisen pitkä puoliintumisaika, ja niiden hajoaminen kestää miljardeja vuosia. Uraani-238:n puoliintumisaika on 4,51 miljardia vuotta. Tämä tarkoittaa, että uraani-238:n hajoaminen puoliksi uraani-238:ksi ja puoliksi torium-234:ksi kestää miljardeja vuosia. Uraani-235:llä (toinen luonnossa esiintyvä uraanin isotooppi) on lyhyempi puoliintumisaika kuin uraani-238:lla, eli vain ~700 miljoonaa vuotta.

Yhtälö

On olemassa yhtälö, jota käytetään usein määrittämään, kuinka paljon tiettyä radioaktiivista ainetta on jäljellä tietyn ajan kuluttua. Tämä määritetään sellaisten ominaisuuksien perusteella kuin aineen puoliintumisaika ja se, kuinka paljon ainetta oli alun perin. Käytetty yhtälö on:

jossa:

• on aineen määrä, kun aikaa on kulunut
• on aineen alkuperäinen määrä
• on kulunut aika
• on aineen puoliintumisaika

Lisäksi vastaavaa yhtälöä voidaan käyttää osoittamaan, miten aineen aktiivisuus vähenee ajan myötä. Kun tämä ilmaistaan, yhtälö on muotoa:

jossa:

• on aineen aktiivisuus sen jälkeen, kun aikaa on kulunut
• on aineen alkuperäinen aktiivisuus
• on kulunut aika
• on aineen puoliintumisaika

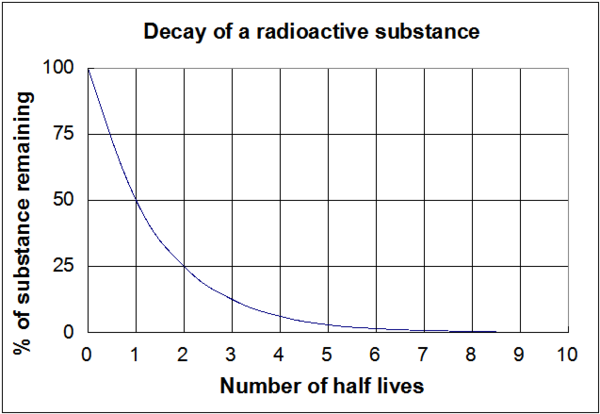
Kuvassa 1 esitetty kuvaaja on visuaalinen esitys näistä yllä olevista yhtälöistä. On tärkeää huomata, että riippumatta puoliintumisajan todellisesta pituudesta (oli se sitten miljoonia vuosia tai muutama nanosekunti) kuvaajan muoto on sama.

Puoliintumisaikojen tunteminen on osa sitä, miten geologit ajoittavat kiviä radioisotooppisella ajoituksella.