Dependent vs Independent Events
Pari viestiä pari viestiä sitten ryhdyin puhumaan todennäköisyydet. Haluan käyttää aiheeseen hieman enemmän aikaa, koska se on yksi niistä käsitteistä, jotka voivat olla yhtenä hetkenä ilmeisen helppoja ja seuraavana hetkenä suorastaan hämmentäviä.
Kun lähestyt todennäköisyysongelmaa, johon liittyy useampi kuin yksi tapahtuma, aloita kysymällä itseltäsi, ovatko tapahtumat toisistaan riippuvaisia vai toisistaan riippumattomia, eli muuttaako yksi tapahtuma toisen tapahtuman todennäköisyyttä? Muuttaako ensimmäinen tapahtuma systeemiä?
(Useiden korttien ottaminen pakasta ilman vaihtoa on klassinen esimerkki riippuvaisesta tapahtumasta. Kun vedämme ensimmäisen kortin, systeemi muuttuu 52 mahdollisesta vaihtoehdosta 51:een ennen kuin toinen tapahtuma tapahtuu.)
Todellisessa elämässä ihmisillä on taipumus sekoittaa riippuvuutta koko ajan. Esimerkiksi heitetään reilua kolikkoa. Se osuu kruunuksi 10 kertaa peräkkäin. Olet varma, että seuraavan kolikon heiton on pakko olla klaava…eikö?
Mikä on todennäköisyys, että seuraava kolikko on taas kruuna?
Se on silti 1/2. Kolikon heittäminen on itsenäinen tapahtuma. Toisin sanoen seuraavan heiton lopputulokseen ei vaikuta se, mitä aiemmin on tapahtunut. Aivan kuin heittäisit kolikkoa ensimmäistä kertaa. Todennäköisyys ei muutu.
Miksi sitten ”tuntuu” siltä, että sen pitäisi olla klaava?
Meillä on tapana ajatella tapahtumia yhdessä, eikä erikseen. Vaikka todennäköisyys heittää kruunaa pysyy samana jokaisella heitolla, 11 kruunan heittämisen yhteenlaskettu todennäköisyys peräkkäin on pieni.
Lasketaan se.
Oppasimme edellisellä todennäköisyysoppitunnilla, että kun niputamme useita tapahtumia yhteen ja haluamme, että ne kaikki tapahtuvat (ja-skenaario), meidän on kerrottava niiden todennäköisyydet yhteen.
Koska jokaisen kolikonheiton todennäköisyys saada kruunu on yhtä suuri kuin 1/2, minun on yksinkertaisesti kerrottava 1/2 yhteen yksitoista kertaa.
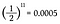
Tämä on 0,05 %:n todennäköisyydellä yksitoista kruunaa peräkkäin! Mutta ennen kuin huokaat helpotuksesta ja sanot: ”Näetkö, minä tiesin sen!”, lasketaan todennäköisyys saada yhdennellätoista heitolla sen sijaan klaava.
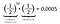
Joo, aivan oikein. On yhtä todennäköistä kääntää kymmenen kruunaa, jota seuraa yksi pyrstö, kuin kääntää yksitoista kruunaa peräkkäin. Itse asiassa, koska kruunan heittämisen yksittäinen todennäköisyys on sama kuin hännän heittämisen todennäköisyys, jokainen 11 kolikonheiton järjestely johtaa samaan todennäköisyyteen 0,0005. Jokainen järjestely on yhtä todennäköinen.
Miksi… miksi kymmenen kruunan heittäminen peräkkäin ”TUNTUU” epätodennäköiseltä?
Yleinen harhaluulo ei johdu todennäköisyydestä, vaan väärinymmärryksestä kombinatoriikasta ja permutaatioista.
Tähän mennessä olemme todenneet, että:
- Todennäköisyydellä kruunan tai klaavan heittämisen todennäköisyydellä on yhtä suuri todennäköisyys jokaisessa yksittäisessä heitossa: P(H) = P(T) = 1/2.
- Jokainen mahdollisten kolikonheittojen ainutkertainen järjestely (permutaatio) on yhtä todennäköinen.
Mitä sitten tapahtuu?
Otoksenotto-avaruuden ymmärtäminen
Otoksenotto-avaruus on yksinkertaisesti kaikkien mahdollisten lopputulosjärjestelyjen (permutaatioiden) luettelo. Koska 11 peräkkäisen kolikonheiton otosavaruus on melko suuri, tarkastellaan sen sijaan yksinkertaisempaa tapausta.
Neljän kolikonheiton otosavaruus on:

Intuitiivisesti voisimme ajatella: On todennäköisempää, että neljästä kolikonheitosta saadaan 2 kruunaa ja 2 klaavaa kuin että saadaan kaikki kruunut tai kaikki klaavat.
Ja tämä on totta. Tehdäänpä matematiikka.
Tiedämme, että jokainen kuudestatoista permutaatiosta on yhtä todennäköinen, koska P(H) = P(T) = 1/2. Jokaisella permutaatiolla on siis yhtä suuri todennäköisyys:

Huomautus: Koska otosavaruus edustaa kaikkia mahdollisia lopputuloksia, kaikkien todennäköisyyksien summa on aina yhtä suuri kuin 1 (Esim. 0,0625 – 16 = 1).
Katsoen otosavaruuttamme, kuinka monta erilaista kolikonheiton permutaatiota johtaa mihin tahansa yhdistelmään 0f 2 kruunaa ja 2 klaavaa?

Huomaa, että 16:sta mahdollisesta lopputuloksesta 6 johtaa kahden pään/kahden hännän yhdistelmään. Koska mikä tahansa näistä kuudesta permutaatiosta täyttää kriteerimme, tätä pidetään ”tai”-skenaariona – joten todennäköisyydet lasketaan yhteen (tai yksinkertaisesti kerrotaan kuudella, koska ne ovat kaikki samat).
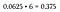
Tämä on 37,5 %:n todennäköisyys heittää kahden kruunun ja kahden pyrstön yhdistelmä, mikä on paljon suurempi kuin todennäköisyys heittää kaikki kruunut tai kaikki pyrstöt (joka on edelleen 6.25 % kummastakin, koska näyteavaruudessamme on vain yksi permutaatio kumpaakin).
Sentähden tiedämme intuitiivisesti, että on todennäköisempää heittää yhtä monta kruunaa ja klaavaa kuin heittää vain yhtä lajia, mutta samalla säilytetään se tosiasia, että tapahtumat ovat toisistaan riippumattomia ja että yksittäiset heittotapahtumat ja permutaatiot ovat yhtä todennäköisiä.
Permutaatiot &Kombinaatiot
Pitkälti menestyksekkääseen todennäköisyyksien laskentaan kuuluu, että ymmärrämme permutaatioita ja kombinaatioita perusteellisesti. Siihen siis suuntaamme seuraavaksi!