L’équation logistique (parfois appelée modèle de Verhulst ou courbe de croissance logistique) est un modèle de croissance démographique publié pour la première fois par Pierre Verhulst (1845, 1847). Le modèle est continu dans le temps, mais une modification de l’équation continue en une équation de récurrence quadratique discrète connue sous le nom de carte logistique est également largement utilisée.
La version continue du modèle logistique est décrite par l’équation différentielle
 |
(1)
|
où 
est le paramètre malthusien (taux de croissance maximale de la population) et 
est ce qu’on appelle la capacité de charge (c’est-à-dire , la population maximale durable). En divisant les deux côtés par 
et en définissant 
, on obtient alors l’équation différentielle
 |
(2)
|
qui est connue sous le nom d’équation logistique. comme l’équation logistique et a pour solution
 |
(3)
|
La fonction 
est parfois connue comme la fonction sigmoïde.
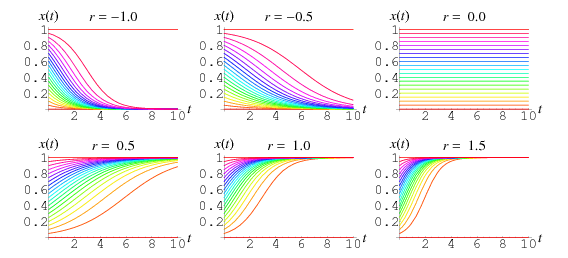
Alors que 
est généralement contrainte d’être positive, des tracés de la solution ci-dessus sont présentés pour diverses valeurs positives et négatives de 
et des conditions initiales 
allant de 0,00 à 1,00 par pas de 0,05.
La version discrète de l’équation logistique (3) est connue comme la carte logistique.
La courbe
 |
(4)
|
obtenue à partir de (3) est parfois connue comme la courbe logistique. De même, une forme normalisée de l’équation (3) est couramment utilisée comme une distribution statistique connue sous le nom de distribution logistique.