Equations du SHM
Considérons un bloc attaché à un ressort sur une table sans friction (Figure \(\PageIndex{3}\)). La position d’équilibre (la position où le ressort n’est ni étiré ni comprimé) est marquée x = 0 . À la position d’équilibre, la force nette est nulle.
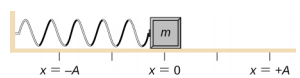
Un travail est effectué sur le bloc pour le tirer jusqu’à une position de x = + A, et il est ensuite libéré du repos. La position maximale de x (A) est appelée l’amplitude du mouvement. Le bloc commence à osciller en SHM entre x = + A et x = -A, où A est l’amplitude du mouvement et T est la période de l’oscillation. La période correspond à la durée d’une oscillation. La figure \(\PageIndex{4}\) montre le mouvement du bloc alors qu’il accomplit une oscillation et demie après le relâchement.
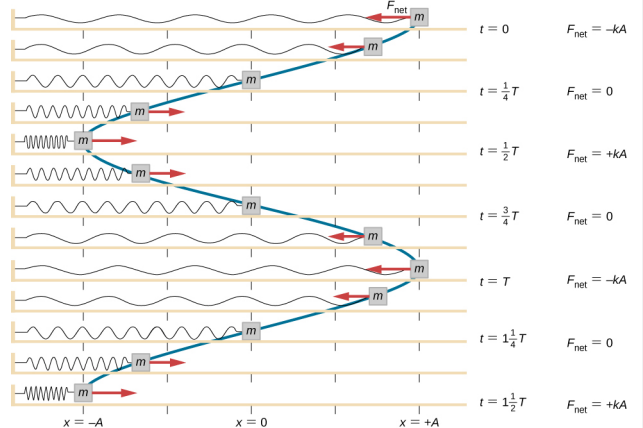
\
L’équation de la position en fonction du temps \(x(t) = A\cos( \omega t)\) est bonne pour modéliser des données, où la position du bloc au temps initial t = 0,00 s est à l’amplitude A et la vitesse initiale est nulle. Souvent, lors de la prise de données expérimentales, la position de la masse au moment initial t = 0,00 s n’est pas égale à l’amplitude et la vitesse initiale n’est pas nulle. Considérons 10 secondes de données recueillies par un étudiant en laboratoire, illustrées sur la figure \(\PageIndex{6}\).
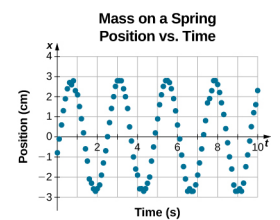
Les données de la figure \(\PageIndex{6}\) peuvent encore être modélisées par une fonction périodique, comme une fonction cosinus, mais la fonction est décalée vers la droite. Ce décalage est connu sous le nom de déphasage et est généralement représenté par la lettre grecque phi (\(\phi\)). L’équation de la position en fonction du temps pour un bloc sur un ressort devient
\
C’est l’équation généralisée pour SHM où t est le temps mesuré en secondes, \(\omega\) est la fréquence angulaire avec des unités de secondes inverses, A est l’amplitude mesurée en mètres ou centimètres, et \(\phi\) est le déphasage mesuré en radians (Figure \(\PageIndex{7}\)). Il convient de noter que, comme les fonctions sinus et cosinus ne diffèrent que par un déphasage, ce mouvement pourrait être modélisé à l’aide de la fonction cosinus ou sinus.
La vitesse de la masse sur un ressort, oscillant en SHM, peut être trouvée en prenant la dérivée de l’équation de position :
Parce que la fonction sinus oscille entre -1 et +1, la vitesse maximale est l’amplitude multipliée par la fréquence angulaire, vmax = A\(\omega\). La vitesse maximale est atteinte à la position d’équilibre (x = 0) lorsque la masse se déplace vers x = + A. La vitesse maximale dans le sens négatif est atteinte à la position d’équilibre (x = 0) lorsque la masse se déplace vers x = -A et est égale à -vmax.
L’accélération de la masse sur le ressort peut être trouvée en prenant la dérivée temporelle de la vitesse :
\
.